Skip to content

Latest commit

 

History

History
215 lines (161 loc) · 7.2 KB

2290.md

File metadata and controls

215 lines (161 loc) · 7.2 KB
Raw
title description keywords
2290. 到达角落需要移除障碍物的最小数目
LeetCode 2290. 到达角落需要移除障碍物的最小数目题解，Minimum Obstacle Removal to Reach Corner，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。
LeetCode
2290. 到达角落需要移除障碍物的最小数目
到达角落需要移除障碍物的最小数目
Minimum Obstacle Removal to Reach Corner
解题思路
广度优先搜索
图
数组
矩阵
最短路
堆（优先队列）

2290. 到达角落需要移除障碍物的最小数目

🔴 Hard  🔖  广度优先搜索 图 数组 矩阵 最短路 堆（优先队列）  🔗 力扣 LeetCode

题目

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

  • 0 represents an empty cell,
  • 1 represents an obstacle that may be removed.

You can move up, down, left, or right from and to an empty cell.

Return _theminimum number of obstacles to remove so you can move from the upper left corner _(0, 0)to the lower right corner(m - 1, n - 1).

Example 1:

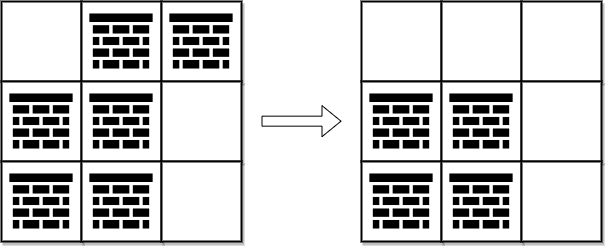
Input: grid = [[0,1,1],[1,1,0],[1,1,0]]

Output: 2

Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).

It can be shown that we need to remove at least 2 obstacles, so we return 2.

Note that there may be other ways to remove 2 obstacles to create a path.

Example 2:

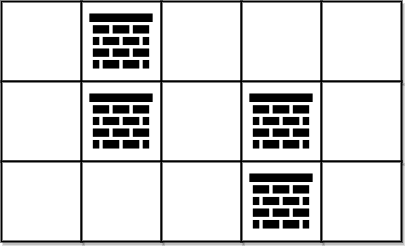
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]

Output: 0

Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 2 <= m * n <= 10^5
  • grid[i][j] is either 0 or 1.
  • grid[0][0] == grid[m - 1][n - 1] == 0

题目大意

给你一个下标从 0 开始的二维整数数组 grid ，数组大小为 m x n 。每个单元格都是两个值之一：

  • 0 表示一个 空 单元格，
  • 1 表示一个可以移除的 障碍物 。

你可以向上、下、左、右移动，从一个空单元格移动到另一个空单元格。

现在你需要从左上角 (0, 0) 移动到右下角 (m - 1, n - 1) ，返回需要移除的障碍物的 最小 数目。

示例 1：

输入： grid = [[0,1,1],[1,1,0],[1,1,0]]

输出： 2

解释： 可以移除位于 (0, 1) 和 (0, 2) 的障碍物来创建从 (0, 0) 到 (2, 2) 的路径。

可以证明我们至少需要移除两个障碍物，所以返回 2 。

注意，可能存在其他方式来移除 2 个障碍物，创建出可行的路径。

示例 2：

输入： grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]

输出： 0

解释： 不移除任何障碍物就能从 (0, 0) 到 (2, 4) ，所以返回 0 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 2 <= m * n <= 10^5
  • grid[i][j] 为 0 或 1
  • grid[0][0] == grid[m - 1][n - 1] == 0

解题思路

这道题可以使用 0-1 BFS 来求解，因为我们需要在移动时最小化移除障碍物的数量。

核心思想是将问题建模为一个加权图，其中：

  • 每个网格单元格 (i, j) 代表图的一个节点。
  • 从一个单元格移动到相邻单元格是图中的边。
    • 如果目标单元格是空单元格，则边的权重为 0。
    • 如果目标单元格是障碍物，则边的权重为 1。

在这种情况下，0-1 BFS 是一种高效的方法：

  • 使用双端队列（Deque）进行广度优先搜索。
  • 先扩展权重为 0 的边（优先队列前部），然后扩展权重为 1 的边（优先队列尾部）。
  • 这样可以保证从起点到终点时遇到的障碍物数量是最小的。

具体算法步骤：

  1. 初始化队列和访问状态：

    • 使用双端队列 deque 存储搜索状态，元素为 [当前行, 当前列, 当前移除的障碍物数量]。
    • 创建一个 visited 数组记录某个位置是否已经访问过，避免重复计算。

  2. 进行 0-1 BFS：

    • 从起点 (0, 0) 开始，将其加入队列，初始移除障碍物数量为 0。
    • 每次从队列中取出一个状态，尝试向上下左右四个方向移动：
      • 如果移动到的单元格是空单元格，将新的状态加入队列的前端。
      • 如果移动到的单元格是障碍物，将新的状态加入队列的后端。
    • 更新访问状态以避免重复访问。

  3. 终止条件：

    • 如果某次扩展到达了终点 (m-1, n-1)，则直接返回当前移除的障碍物数量。

  4. 返回结果：

    • 如果队列为空仍未到达终点，说明不存在路径。

复杂度分析

  • 时间复杂度：O(m * n)，其中 m 是行数，n 是列数，每个单元格最多会被访问一次，
  • 空间复杂度：O(m * n)，使用了一个 visited 哈希 Set 来记录访问状态，空间复杂度为 O(m * n)。另外，双端队列的空间复杂度最多为 O(m * n)。

代码

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minimumObstacles = function (grid) {
	const m = grid.length,
		n = grid[0].length;
	const directions = [
		[1, 0],
		[-1, 0],
		[0, 1],
		[0, -1]
	]; // 四个方向
	const deque = new Deque([[0, 0, 0]]); // 初始状态：行、列、移除障碍物数
	const visited = new Set(['0,0']);

	while (!deque.isEmpty()) {
		const [x, y, obstacles] = deque.popFront();

		// 如果到达终点，直接返回当前移除障碍物的数量
		if (x === m - 1 && y === n - 1) return obstacles;

		for (const [dx, dy] of directions) {
			const nx = x + dx,
				ny = y + dy;

			// 检查是否越界以及是否已访问
			if (
				nx >= 0 &&
				nx < m &&
				ny >= 0 &&
				ny < n &&
				!visited.has(`${nx},${ny}`)
			) {
				visited.add(`${nx},${ny}`); // 标记为已访问

				// 空单元格优先处理
				if (grid[nx][ny] === 0) {
					deque.pushFront([nx, ny, obstacles]);
				} else {
					deque.pushBack([nx, ny, obstacles + 1]);
				}
			}
		}
	}

	return -1; // 不可能到达终点
};

相关题目

题号 标题 题解 标签 难度 力扣
1293 网格中的最短路径 广度优先搜索 数组 矩阵 🔴 🀄️ 🔗