Skip to content

Latest commit

 

History

History
205 lines (155 loc) · 8.29 KB

2641.md

File metadata and controls

205 lines (155 loc) · 8.29 KB
Raw
title description keywords
2641. 二叉树的堂兄弟节点 II
LeetCode 2641. 二叉树的堂兄弟节点 II题解，Cousins in Binary Tree II，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。
LeetCode
2641. 二叉树的堂兄弟节点 II
二叉树的堂兄弟节点 II
Cousins in Binary Tree II
解题思路
树
深度优先搜索
广度优先搜索
哈希表
二叉树

2641. 二叉树的堂兄弟节点 II

🟠 Medium  🔖  树 深度优先搜索 广度优先搜索 哈希表 二叉树  🔗 力扣 LeetCode

题目

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins ' values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return theroot of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

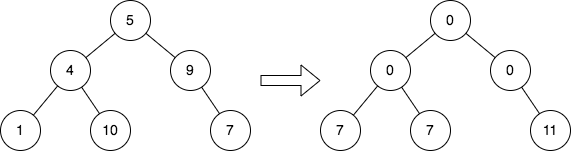
Input: root = [5,4,9,1,10,null,7]

Output: [0,0,0,7,7,null,11]

Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.

  • Node with value 5 does not have any cousins so its sum is 0.
  • Node with value 4 does not have any cousins so its sum is 0.
  • Node with value 9 does not have any cousins so its sum is 0.
  • Node with value 1 has a cousin with value 7 so its sum is 7.
  • Node with value 10 has a cousin with value 7 so its sum is 7.
  • Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]

Output: [0,0,0]

Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.

  • Node with value 3 does not have any cousins so its sum is 0.
  • Node with value 1 does not have any cousins so its sum is 0.
  • Node with value 2 does not have any cousins so its sum is 0.

Constraints:

  • The number of nodes in the tree is in the range [1, 10^5].
  • 1 <= Node.val <= 10^4

题目大意

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 **堂兄弟节点值的和 **。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意 ，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

输入： root = [5,4,9,1,10,null,7]

输出：[0,0,0,7,7,null,11]

解释： 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。

  • 值为 5 的节点没有堂兄弟，所以值修改为 0 。
  • 值为 4 的节点没有堂兄弟，所以值修改为 0 。
  • 值为 9 的节点没有堂兄弟，所以值修改为 0 。
  • 值为 1 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
  • 值为 10 的节点有一个堂兄弟，值为 7 ，所以值修改为 7 。
  • 值为 7 的节点有两个堂兄弟，值分别为 1 和 10 ，所以值修改为 11 。

示例 2：

输入： root = [3,1,2]

输出：[0,0,0]

解释： 上图展示了初始的二叉树和修改每个节点的值之后的二叉树。

  • 值为 3 的节点没有堂兄弟，所以值修改为 0 。
  • 值为 1 的节点没有堂兄弟，所以值修改为 0 。
  • 值为 2 的节点没有堂兄弟，所以值修改为 0 。

提示：

  • 树中节点数目的范围是 [1, 10^5] 。
  • 1 <= Node.val <= 10^4

解题思路

在你的代码中，，其中：

  • node：表示当前遍历到的树节点，它是一个 TreeNode 对象，包含节点的值以及指向其左子节点和右子节点的指针。
  • siblingSum：表示当前节点的兄弟节点的值之和。这个值是根据当前节点的父节点计算得出的，即父节点的左右子节点的值之和（不包括当前节点自身）。

存储过程

  1. 初始化：
  • 首先，检查根节点是否存在。如果不存在，则直接返回 null。
  • 创建一个队列，每个节点以一个数组的形式存储，具体结构为 [node, siblingSum]，其中：
    • node：表示当前遍历到的树节点，它是一个 TreeNode 对象，包含节点的值以及指向其左子节点和右子节点的指针。
    • siblingSum：表示和当前节点的父节点相同的兄弟节点的值之和（包括当前节点自身），这个值是根据当前节点的父节点计算得出的，即父节点的左右子节点的值之和。
  • 在 BFS 开始时，将根节点及其值 root.val 存入队列，初始化队列为 [[root, root.val]]。

  1. 广度优先搜索 (BFS)：

    • 进行 BFS 遍历，每次从队列中取出当前层的所有节点，存储在 currentLevel 中，然后按层存入 levels 数组。

  2. 更新节点值：

    • 遍历 levels 数组，计算当前层所有节点值的总和，存储在 totalSum 变量中，以便后续更新每个节点的值。
    • 遍历当前层的所有节点，将每个节点的值更新为 totalSum 减去该节点的兄弟节点值和，这样确保了每个节点的新值是其同层堂兄弟节点的和。

  3. 返回结果：

    • 完成所有层的遍历和更新后，返回更新后的根节点 root。

复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点数量吗，对树中每个节点只进行一次访问。
  • 空间复杂度：O(n)
    • BFS 使用队列存储当前层的节点，而在最坏情况下（例如完全二叉树），队列可能存储所有节点。因此空间复杂度为 O(n)。
    • 另外，levels 数组也存储每一层的节点引用和兄弟节点值和，在最坏情况下也会占用 O(n) 的空间。

代码

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var replaceValueInTree = function (root) {
	if (!root) return null;
	// 初始化队列
	let queue = [[root, root.val]],
		levels = [];

	// BFS
	while (queue.length) {
		const len = queue.length;
		let currentLevel = [];
		for (let i = 0; i < len; i++) {
			// 从队列中取出当前层的所有节点，存入 currentLevel 中
			const [node, siblingSum] = queue.shift();
			currentLevel.push([node, siblingSum]);

			// 计算相同父节点的兄弟节点的值之和
			const childSum =
				(node.left ? node.left.val : 0) + (node.right ? node.right.val : 0);
			if (node.left) queue.push([node.left, childSum]);
			if (node.right) queue.push([node.right, childSum]);
		}

		// 按层存入 levels 数组
		levels.push(currentLevel);
	}

	for (let i = 0; i < levels.length; i++) {
		const currentLevel = levels[i];
		// 计算当前层所有节点值的总和
		const totalSum = currentLevel.reduce((acc, cur) => acc + cur[0].val, 0);
		for (let [node, siblingSum] of currentLevel) {
			// 新的值为 totalSum 减去该节点的同父兄弟节点值之和
			node.val = totalSum - siblingSum;
		}
	}

	return root;
};

相关题目

题号 标题 题解 标签 难度 力扣
993 二叉树的堂兄弟节点 [✓] 树 深度优先搜索 广度优先搜索 1+ 🟢 🀄️ 🔗
1161 最大层内元素和 [✓] 树 深度优先搜索 广度优先搜索 1+ 🟠 🀄️ 🔗