Skip to content

Latest commit

 

History

History
494 lines (394 loc) · 13.2 KB

0700.二叉搜索树中的搜索.md

File metadata and controls

494 lines (394 loc) · 13.2 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

700.二叉搜索树中的搜索

力扣题目地址

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，

700.二叉搜索树中的搜索

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

算法公开课

《代码随想录》算法视频公开课：不愧是搜索树，这次搜索有方向了！| LeetCode：700.二叉搜索树中的搜索，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

之前我们讲的都是普通二叉树，那么接下来看看二叉搜索树。

在关于二叉树，你该了解这些！中，我们已经讲过了二叉搜索树。

二叉搜索树是一个有序树：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

本题，其实就是在二叉搜索树中搜索一个节点。那么我们来看看应该如何遍历。

递归法

  1. 确定递归函数的参数和返回值

递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

代码如下：

TreeNode* searchBST(TreeNode* root, int val)
  1. 确定终止条件

如果root为空，或者找到这个数值了，就返回root节点。

if (root == NULL || root->val == val) return root;
  1. 确定单层递归的逻辑

看看二叉搜索树的单层递归逻辑有何不同。

因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。

代码如下：

TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;

很多录友写递归函数的时候 习惯直接写 searchBST(root->left, val)，却忘了 递归函数还有返回值。

递归函数的返回值是什么? 是 左子树如果搜索到了val，要将该节点返回。 如果不用一个变量将其接住，那么返回值不就没了。

所以要 result = searchBST(root->left, val)。

整体代码如下：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        TreeNode* result = NULL;
        if (root->val > val) result = searchBST(root->left, val);
        if (root->val < val) result = searchBST(root->right, val);
        return result;
    }
};

或者我们也可以这么写

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        if (root->val > val) return searchBST(root->left, val);
        if (root->val < val) return searchBST(root->right, val);
        return NULL;
    }
};

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。

对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

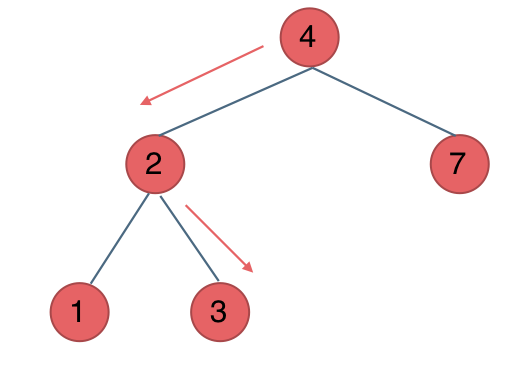
例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。

中间节点如果大于3就向左走，如果小于3就向右走，如图：

二叉搜索树

所以迭代法代码如下：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return NULL;
    }
};

第一次看到了如此简单的迭代法，是不是感动的痛哭流涕，哭一会~

总结

本篇我们介绍了二叉搜索树的遍历方式，因为二叉搜索树的有序性，遍历的时候要比普通二叉树简单很多。

但是一些同学很容易忽略二叉搜索树的特性，所以写出遍历的代码就未必真的简单了。

所以针对二叉搜索树的题目，一样要利用其特性。

文中我依然给出递归和迭代两种方式，可以看出写法都非常简单，就是利用了二叉搜索树有序的特点。

其他语言版本

Java

class Solution {
    // 递归，普通二叉树
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        TreeNode left = searchBST(root.left, val);
        if (left != null) {
            return left;
        }
        return searchBST(root.right, val);
    }
}

class Solution {
    // 递归，利用二叉搜索树特点，优化
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        if (val < root.val) {
            return searchBST(root.left, val);
        } else {
            return searchBST(root.right, val);
        }
    }
}

class Solution {
    // 迭代，普通二叉树
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode pop = stack.pop();
            if (pop.val == val) {
                return pop;
            }
            if (pop.right != null) {
                stack.push(pop.right);
            }
            if (pop.left != null) {
                stack.push(pop.left);
            }
        }
        return null;
    }
}

class Solution {
    // 迭代，利用二叉搜索树特点，优化，可以不需要栈
    public TreeNode searchBST(TreeNode root, int val) {
        while (root != null)
            if (val < root.val) root = root.left;
            else if (val > root.val) root = root.right;
            else return root;
        return null;
    }
}

Python

（方法一） 递归

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        # 为什么要有返回值: 
        #   因为搜索到目标节点就要立即return，
        #   这样才是找到节点就返回（搜索某一条边），如果不加return，就是遍历整棵树了。

        if not root or root.val == val: 
            return root

        if root.val > val: 
            return self.searchBST(root.left, val)

        if root.val < val: 
            return self.searchBST(root.right, val)

（方法二）迭代

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root:
            if val < root.val: root = root.left
            elif val > root.val: root = root.right
            else: return root
        return None

Go

递归法：

 //递归法
func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil || root.Val == val {
        return root
    }
    if root.Val > val {
        return searchBST(root.Left, val)
    }
    return searchBST(root.Right, val)
}

迭代法：

 //迭代法
func searchBST(root *TreeNode, val int) *TreeNode {
    for root != nil {
        if root.Val > val {
            root = root.Left
        } else if root.Val < val {
            root = root.Right
        } else {
            return root
        }
    }
    return nil
}

JavaScript

递归：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    if (!root || root.val === val) {
        return root;
    }
    if (root.val > val)
        return searchBST(root.left, val);
    if (root.val < val)
        return searchBST(root.right, val);
};

迭代：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    while (root !== null) {
        if (root.val > val)
            root = root.left;
        else if (root.val < val)
            root = root.right;
        else 
            return root;
    }
    return null;
};

TypeScript

递归法

function searchBST(root: TreeNode | null, val: number): TreeNode | null {
    if (root === null || root.val === val) return root;
    if (root.val < val) return searchBST(root.right, val);
    if (root.val > val) return searchBST(root.left, val);
    return null;
};

迭代法

function searchBST(root: TreeNode | null, val: number): TreeNode | null {
    let resNode: TreeNode | null = root;
    while (resNode !== null) {
        if (resNode.val === val) return resNode;
        if (resNode.val < val) {
            resNode = resNode.right;
        } else {
            resNode = resNode.left;
        }
    }
    return null;
};

Scala

递归:

object Solution {
  def searchBST(root: TreeNode, value: Int): TreeNode = {
    if (root == null || value == root.value) return root
    // 相当于三元表达式，在Scala中if...else有返回值
    if (value < root.value) searchBST(root.left, value) else searchBST(root.right, value)
  }
}

迭代:

object Solution {
  def searchBST(root: TreeNode, value: Int): TreeNode = {
    // 因为root是不可变量，所以需要赋值给一个可变量
    var node = root
    while (node != null) {
      if (value < node.value) node = node.left
      else if (value > node.value) node = node.right
      else return node
    }
    null // 没有返回就返回空
  }
}

Rust

递归：

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn search_bst(
        root: Option<Rc<RefCell<TreeNode>>>,
        val: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        if root.is_none() || root.as_ref().unwrap().borrow().val == val {
            return root;
        }
        let node_val = root.as_ref().unwrap().borrow().val;
        if node_val > val {
            return Self::search_bst(root.as_ref().unwrap().borrow().left.clone(), val);
        }
        if node_val < val {
            return Self::search_bst(root.unwrap().borrow().right.clone(), val);
        }
        None
    }
}

迭代：

use std::cell::RefCell;
use std::rc::Rc;
use std::cmp;
impl Solution {
    pub fn search_bst(
        mut root: Option<Rc<RefCell<TreeNode>>>,
        val: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        while let Some(ref node) = root.clone() {
            match val.cmp(&node.borrow().val) {
                cmp::Ordering::Less => root = node.borrow().left.clone(),
                cmp::Ordering::Equal => return root,
                cmp::Ordering::Greater => root = node.borrow().right.clone(),
            };
        }
        None
    }
}

C#

// 递归
public TreeNode SearchBST(TreeNode root, int val)
{
    if (root == null || root.val == val) return root;
    if (root.val > val) return SearchBST(root.left, val);
    if (root.val < val) return SearchBST(root.right, val);
    return null;
}
//  迭代
public TreeNode SearchBST(TreeNode root, int val)
{
    while (root != null)
    {
        if (root.val > val) root = root.left;
        else if (root.val < val) root = root.right;
        else return root;
    }
    return null;
}