| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
中等 |
|
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
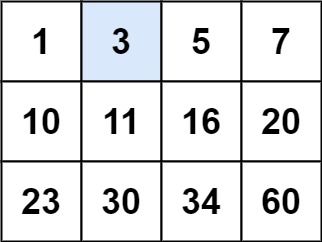
示例 1:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
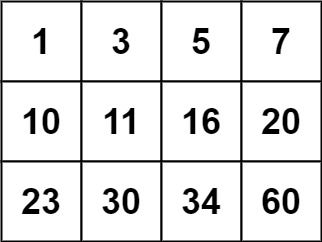
示例 2:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
我们将二维矩阵逻辑展开,然后二分查找即可。
时间复杂度
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m, n = len(matrix), len(matrix[0])
left, right = 0, m * n - 1
while left < right:
mid = (left + right) >> 1
x, y = divmod(mid, n)
if matrix[x][y] >= target:
right = mid
else:
left = mid + 1
return matrix[left // n][left % n] == targetclass Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int left = 0, right = m * n - 1;
while (left < right) {
int mid = (left + right) >> 1;
int x = mid / n, y = mid % n;
if (matrix[x][y] >= target) {
right = mid;
} else {
left = mid + 1;
}
}
return matrix[left / n][left % n] == target;
}
}class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int left = 0, right = m * n - 1;
while (left < right) {
int mid = left + right >> 1;
int x = mid / n, y = mid % n;
if (matrix[x][y] >= target) {
right = mid;
} else {
left = mid + 1;
}
}
return matrix[left / n][left % n] == target;
}
};func searchMatrix(matrix [][]int, target int) bool {
m, n := len(matrix), len(matrix[0])
left, right := 0, m*n-1
for left < right {
mid := (left + right) >> 1
x, y := mid/n, mid%n
if matrix[x][y] >= target {
right = mid
} else {
left = mid + 1
}
}
return matrix[left/n][left%n] == target
}function searchMatrix(matrix: number[][], target: number): boolean {
const m = matrix.length;
const n = matrix[0].length;
let left = 0;
let right = m * n;
while (left < right) {
const mid = (left + right) >>> 1;
const i = Math.floor(mid / n);
const j = mid % n;
if (matrix[i][j] === target) {
return true;
}
if (matrix[i][j] < target) {
left = mid + 1;
} else {
right = mid;
}
}
return false;
}use std::cmp::Ordering;
impl Solution {
pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
let m = matrix.len();
let n = matrix[0].len();
let mut i = 0;
let mut j = n;
while i < m && j > 0 {
match matrix[i][j - 1].cmp(&target) {
Ordering::Equal => {
return true;
}
Ordering::Less => {
i += 1;
}
Ordering::Greater => {
j -= 1;
}
}
}
false
}
}/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function (matrix, target) {
const m = matrix.length,
n = matrix[0].length;
let left = 0,
right = m * n - 1;
while (left < right) {
const mid = (left + right + 1) >> 1;
const x = Math.floor(mid / n);
const y = mid % n;
if (matrix[x][y] <= target) {
left = mid;
} else {
right = mid - 1;
}
}
return matrix[Math.floor(left / n)][left % n] == target;
};这里我们以左下角作为起始搜索点,往右上方向开始搜索,比较当前元素
- 若
$matrix[i][j] = target$ ,说明找到了目标值,直接返回true。 - 若
$matrix[i][j] > target$ ,说明这一行从当前位置开始往右的所有元素均大于 target,应该让 i 指针往上移动,即$i = i - 1$ 。 - 若
$matrix[i][j] < target$ ,说明这一列从当前位置开始往上的所有元素均小于 target,应该让 j 指针往右移动,即$j = j + 1$ 。
若搜索结束依然找不到 false。
时间复杂度
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m, n = len(matrix), len(matrix[0])
i, j = m - 1, 0
while i >= 0 and j < n:
if matrix[i][j] == target:
return True
if matrix[i][j] > target:
i -= 1
else:
j += 1
return Falseclass Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
for (int i = m - 1, j = 0; i >= 0 && j < n;) {
if (matrix[i][j] == target) {
return true;
}
if (matrix[i][j] > target) {
--i;
} else {
++j;
}
}
return false;
}
}class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
for (int i = m - 1, j = 0; i >= 0 && j < n;) {
if (matrix[i][j] == target) return true;
if (matrix[i][j] > target)
--i;
else
++j;
}
return false;
}
};func searchMatrix(matrix [][]int, target int) bool {
m, n := len(matrix), len(matrix[0])
for i, j := m-1, 0; i >= 0 && j < n; {
if matrix[i][j] == target {
return true
}
if matrix[i][j] > target {
i--
} else {
j++
}
}
return false
}use std::cmp::Ordering;
impl Solution {
pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
let m = matrix.len();
let n = matrix[0].len();
let mut left = 0;
let mut right = m * n;
while left < right {
let mid = left + (right - left) / 2;
let i = mid / n;
let j = mid % n;
match matrix[i][j].cmp(&target) {
Ordering::Equal => {
return true;
}
Ordering::Less => {
left = mid + 1;
}
Ordering::Greater => {
right = mid;
}
}
}
false
}
}/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function (matrix, target) {
const m = matrix.length,
n = matrix[0].length;
for (let i = m - 1, j = 0; i >= 0 && j < n; ) {
if (matrix[i][j] == target) {
return true;
}
if (matrix[i][j] > target) {
--i;
} else {
++j;
}
}
return false;
};