| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
简单 |
|
给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
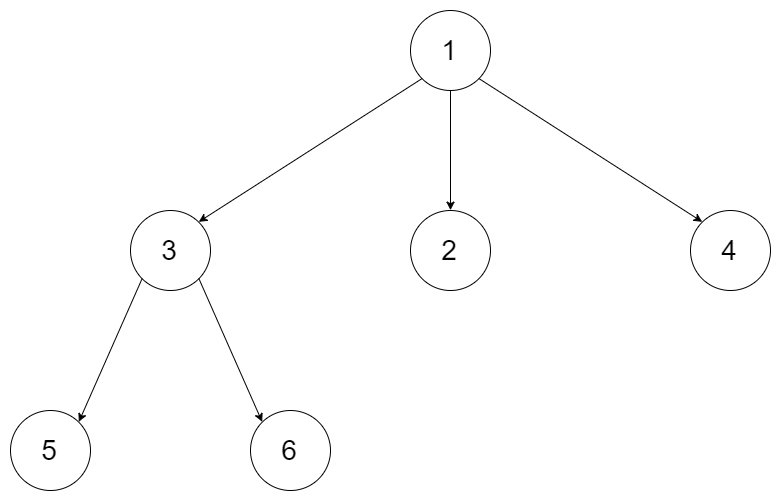
示例 1:
输入:root = [1,null,3,2,4,null,5,6] 输出:[1,3,5,6,2,4]
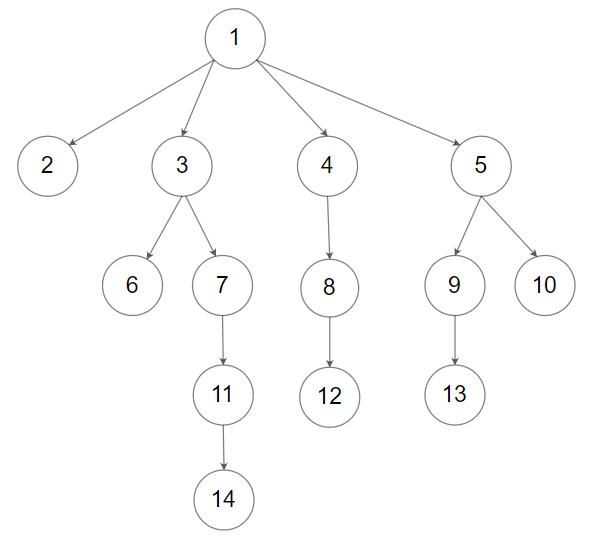
示例 2:
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[1,2,3,6,7,11,14,4,8,12,5,9,13,10]
提示:
- 节点总数在范围
[0, 104]内 0 <= Node.val <= 104- n 叉树的高度小于或等于
1000
进阶:递归法很简单,你可以使用迭代法完成此题吗?
我们可以递归地遍历整棵树。对于每个节点,先将节点的值加入答案,然后对该节点的每个子节点递归地调用函数。
时间复杂度
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: "Node") -> List[int]:
def dfs(root):
if root is None:
return
ans.append(root.val)
for child in root.children:
dfs(child)
ans = []
dfs(root)
return ans/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
private List<Integer> ans = new ArrayList<>();
public List<Integer> preorder(Node root) {
dfs(root);
return ans;
}
private void dfs(Node root) {
if (root == null) {
return;
}
ans.add(root.val);
for (Node child : root.children) {
dfs(child);
}
}
}/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> ans;
function<void(Node*)> dfs = [&](Node* root) {
if (!root) {
return;
}
ans.push_back(root->val);
for (auto& child : root->children) {
dfs(child);
}
};
dfs(root);
return ans;
}
};/**
* Definition for a Node.
* type Node struct {
* Val int
* Children []*Node
* }
*/
func preorder(root *Node) (ans []int) {
var dfs func(*Node)
dfs = func(root *Node) {
if root == nil {
return
}
ans = append(ans, root.Val)
for _, child := range root.Children {
dfs(child)
}
}
dfs(root)
return
}/**
* Definition for node.
* class Node {
* val: number
* children: Node[]
* constructor(val?: number) {
* this.val = (val===undefined ? 0 : val)
* this.children = []
* }
* }
*/
function preorder(root: Node | null): number[] {
const ans: number[] = [];
const dfs = (root: Node | null) => {
if (!root) {
return;
}
ans.push(root.val);
for (const child of root.children) {
dfs(child);
}
};
dfs(root);
return ans;
}/**
* Definition for a Node.
* struct Node {
* int val;
* int numChildren;
* struct Node** children;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
void dfs(struct Node* root, int* ans, int* i) {
if (!root) {
return;
}
ans[(*i)++] = root->val;
for (int j = 0; j < root->numChildren; j++) {
dfs(root->children[j], ans, i);
}
}
int* preorder(struct Node* root, int* returnSize) {
int* ans = malloc(sizeof(int) * 10000);
*returnSize = 0;
dfs(root, ans, returnSize);
return ans;
}我们也可以用迭代的方法来解决这个问题。
我们使用一个栈来帮助我们得到前序遍历,我们首先把根节点入栈,因为前序遍历是根节点、左子树、右子树,栈的特点是先进后出,所以我们先把节点的值加入答案,然后对该节点的每个子节点按照从右到左的顺序依次入栈。循环直到栈为空。
时间复杂度
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: 'Node') -> List[int]:
ans = []
if root is None:
return ans
stk = [root]
while stk:
node = stk.pop()
ans.append(node.val)
for child in node.children[::-1]:
stk.append(child)
return ans/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<Integer> preorder(Node root) {
if (root == null) {
return Collections.emptyList();
}
List<Integer> ans = new ArrayList<>();
Deque<Node> stk = new ArrayDeque<>();
stk.push(root);
while (!stk.isEmpty()) {
Node node = stk.pop();
ans.add(node.val);
List<Node> children = node.children;
for (int i = children.size() - 1; i >= 0; --i) {
stk.push(children.get(i));
}
}
return ans;
}
}/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<int> preorder(Node* root) {
if (!root) return {};
vector<int> ans;
stack<Node*> stk;
stk.push(root);
while (!stk.empty()) {
Node* node = stk.top();
ans.push_back(node->val);
stk.pop();
auto children = node->children;
for (int i = children.size() - 1; i >= 0; --i) stk.push(children[i]);
}
return ans;
}
};/**
* Definition for a Node.
* type Node struct {
* Val int
* Children []*Node
* }
*/
func preorder(root *Node) (ans []int) {
if root == nil {
return
}
stk := []*Node{root}
for len(stk) > 0 {
node := stk[len(stk)-1]
ans = append(ans, node.Val)
stk = stk[:len(stk)-1]
children := node.Children
for i := len(children) - 1; i >= 0; i-- {
stk = append(stk, children[i])
}
}
return
}/**
* Definition for node.
* class Node {
* val: number
* children: Node[]
* constructor(val?: number) {
* this.val = (val===undefined ? 0 : val)
* this.children = []
* }
* }
*/
function preorder(root: Node | null): number[] {
const ans: number[] = [];
if (!root) {
return ans;
}
const stk: Node[] = [root];
while (stk.length) {
const { val, children } = stk.pop()!;
ans.push(val);
for (let i = children.length - 1; i >= 0; i--) {
stk.push(children[i]);
}
}
return ans;
}