README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0800-0899/0835.Image%20Overlap/README.md	数组 矩阵

835. 图像重叠

English Version

题目描述

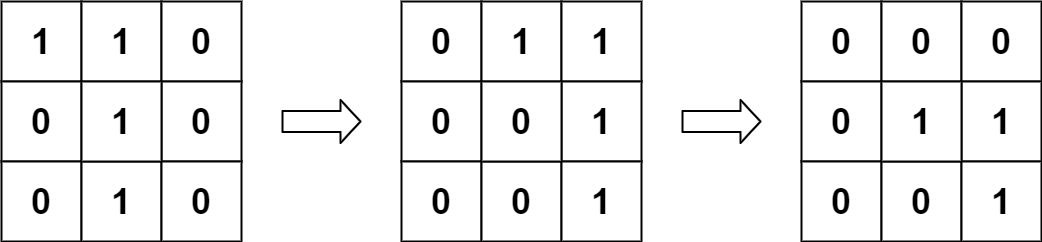
给你两个图像 img1 和 img2 ，两个图像的大小都是 n x n ，用大小相同的二进制正方形矩阵表示。二进制矩阵仅由若干 0 和若干 1 组成。

转换 其中一个图像，将所有的 1 向左，右，上，或下滑动任何数量的单位；然后把它放在另一个图像的上面。该转换的 重叠 是指两个图像 都 具有 1 的位置的数目。

请注意，转换 不包括 向任何方向旋转。越过矩阵边界的 1 都将被清除。

最大可能的重叠数量是多少？

 

示例 1：

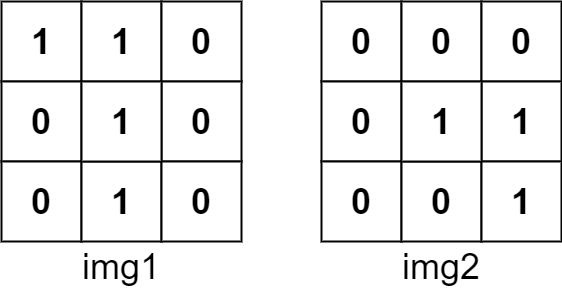
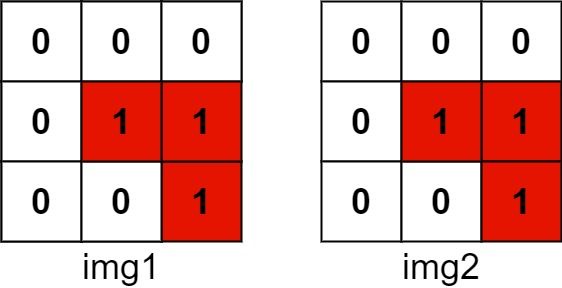
输入：img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
输出：3
解释：将 img1 向右移动 1 个单位，再向下移动 1 个单位。

两个图像都具有 1 的位置的数目是 3（用红色标识）。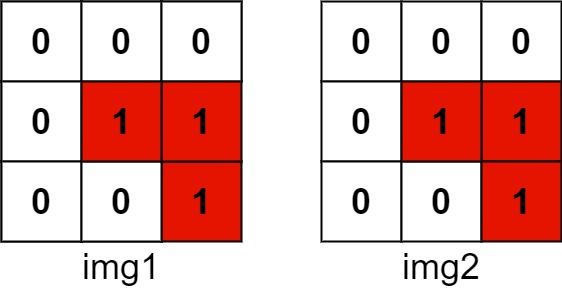

示例 2：

输入：img1 = [[1]], img2 = [[1]]
输出：1

示例 3：

输入：img1 = [[0]], img2 = [[0]]
输出：0

 

提示：

• n == img1.length == img1[i].length
• n == img2.length == img2[i].length
• 1 <= n <= 30
• img1[i][j] 为 0 或 1
• img2[i][j] 为 0 或 1

解法

方法一：枚举

我们可以枚举 $img1$ 和 $img2$ 的每个 $1$ 的位置，分别记为 $(i, j)$ 和 $(h, k)$。然后我们计算得到偏移量 $(i - h, j - k)$，记为 $(dx, dy)$，用哈希表 $cnt$ 记录每个偏移量出现的次数。最后我们遍历哈希表 $cnt$，找到出现次数最多的偏移量，即为答案。

时间复杂度 $O(n^4)$，空间复杂度 $O(n^2)$。其中 $n$ 是 $img1$ 的边长。

Python3

class Solution:
    def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:
        n = len(img1)
        cnt = Counter()
        for i in range(n):
            for j in range(n):
                if img1[i][j]:
                    for h in range(n):
                        for k in range(n):
                            if img2[h][k]:
                                cnt[(i - h, j - k)] += 1
        return max(cnt.values()) if cnt else 0

Java

class Solution {
    public int largestOverlap(int[][] img1, int[][] img2) {
        int n = img1.length;
        Map<List<Integer>, Integer> cnt = new HashMap<>();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (img1[i][j] == 1) {
                    for (int h = 0; h < n; ++h) {
                        for (int k = 0; k < n; ++k) {
                            if (img2[h][k] == 1) {
                                List<Integer> t = List.of(i - h, j - k);
                                ans = Math.max(ans, cnt.merge(t, 1, Integer::sum));
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) {
        int n = img1.size();
        map<pair<int, int>, int> cnt;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (img1[i][j]) {
                    for (int h = 0; h < n; ++h) {
                        for (int k = 0; k < n; ++k) {
                            if (img2[h][k]) {
                                ans = max(ans, ++cnt[{i - h, j - k}]);
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
};

Go

func largestOverlap(img1 [][]int, img2 [][]int) (ans int) {
	type pair struct{ x, y int }
	cnt := map[pair]int{}
	for i, row1 := range img1 {
		for j, x1 := range row1 {
			if x1 == 1 {
				for h, row2 := range img2 {
					for k, x2 := range row2 {
						if x2 == 1 {
							t := pair{i - h, j - k}
							cnt[t]++
							ans = max(ans, cnt[t])
						}
					}
				}
			}
		}
	}
	return
}

TypeScript

function largestOverlap(img1: number[][], img2: number[][]): number {
    const n = img1.length;
    const cnt: Map<number, number> = new Map();
    let ans = 0;
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            if (img1[i][j] === 1) {
                for (let h = 0; h < n; ++h) {
                    for (let k = 0; k < n; ++k) {
                        if (img2[h][k] === 1) {
                            const t = (i - h) * 200 + (j - k);
                            cnt.set(t, (cnt.get(t) ?? 0) + 1);
                            ans = Math.max(ans, cnt.get(t)!);
                        }
                    }
                }
            }
        }
    }
    return ans;
}