| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
困难 |
2449 |
第 274 场周赛 Q4 |
|
一个公司准备组织一场会议,邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子,可以坐下 任意数目 的员工。
员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工,每位员工 当且仅当 他被安排在喜欢员工的旁边,他才会参加会议。每位员工喜欢的员工 不会 是他自己。
给你一个下标从 0 开始的整数数组 favorite ,其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。
示例 1:
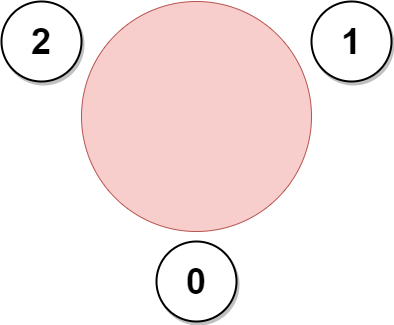
输入:favorite = [2,2,1,2] 输出:3 解释: 上图展示了公司邀请员工 0,1 和 2 参加会议以及他们在圆桌上的座位。 没办法邀请所有员工参与会议,因为员工 2 没办法同时坐在 0,1 和 3 员工的旁边。 注意,公司也可以邀请员工 1,2 和 3 参加会议。 所以最多参加会议的员工数目为 3 。
示例 2:
输入:favorite = [1,2,0] 输出:3 解释: 每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。 座位安排同图 1 所示: - 员工 0 坐在员工 2 和 1 之间。 - 员工 1 坐在员工 0 和 2 之间。 - 员工 2 坐在员工 1 和 0 之间。 参与会议的最多员工数目为 3 。
示例 3:
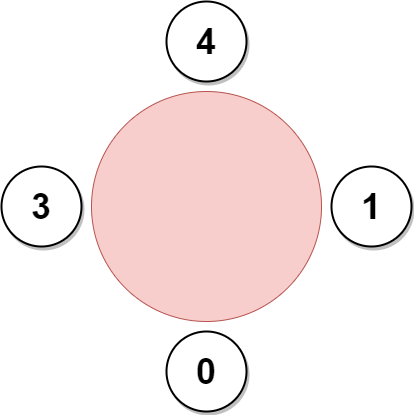
输入:favorite = [3,0,1,4,1] 输出:4 解释: 上图展示了公司可以邀请员工 0,1,3 和 4 参加会议以及他们在圆桌上的座位。 员工 2 无法参加,因为他喜欢的员工 1 旁边的座位已经被占领了。 所以公司只能不邀请员工 2 。 参加会议的最多员工数目为 4 。
提示:
n == favorite.length2 <= n <= 1050 <= favorite[i] <= n - 1favorite[i] != i
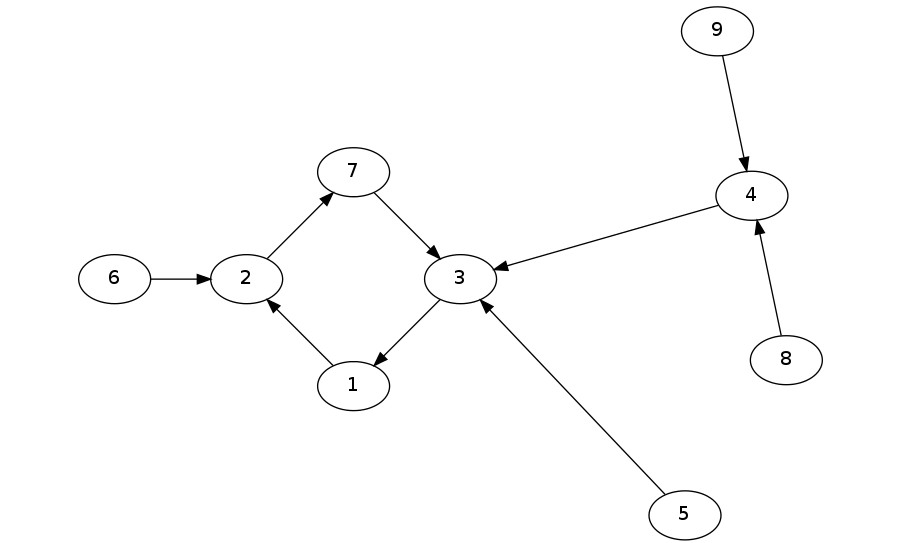
我们观察发现,题目中员工的喜好关系可以看作一个有向图,这个有向图可以分成多个“基环内向树”的结构。在每个结构中,包含一个环,而环上的每个节点都连接着一棵树。
什么是“基环内向树”?首先,基环树是一个具有
对于本题,我们可以求出图的最大环的长度,这里我们只需要求出最大的一个环的长度,这是因为,如果有多个环,那么不同环之间是不连通的,不符合题意。
另外,对于环的大小等于
因此,问题实际上等价于求出图的最大环的长度,以及所有长度为
时间复杂度 favorite 的长度。
相似题目:
class Solution:
def maximumInvitations(self, favorite: List[int]) -> int:
def max_cycle(fa: List[int]) -> int:
n = len(fa)
vis = [False] * n
ans = 0
for i in range(n):
if vis[i]:
continue
cycle = []
j = i
while not vis[j]:
cycle.append(j)
vis[j] = True
j = fa[j]
for k, v in enumerate(cycle):
if v == j:
ans = max(ans, len(cycle) - k)
break
return ans
def topological_sort(fa: List[int]) -> int:
n = len(fa)
indeg = [0] * n
dist = [1] * n
for v in fa:
indeg[v] += 1
q = deque(i for i, v in enumerate(indeg) if v == 0)
while q:
i = q.popleft()
dist[fa[i]] = max(dist[fa[i]], dist[i] + 1)
indeg[fa[i]] -= 1
if indeg[fa[i]] == 0:
q.append(fa[i])
return sum(dist[i] for i, v in enumerate(fa) if i == fa[fa[i]])
return max(max_cycle(favorite), topological_sort(favorite))class Solution {
public int maximumInvitations(int[] favorite) {
return Math.max(maxCycle(favorite), topologicalSort(favorite));
}
private int maxCycle(int[] fa) {
int n = fa.length;
boolean[] vis = new boolean[n];
int ans = 0;
for (int i = 0; i < n; ++i) {
if (vis[i]) {
continue;
}
List<Integer> cycle = new ArrayList<>();
int j = i;
while (!vis[j]) {
cycle.add(j);
vis[j] = true;
j = fa[j];
}
for (int k = 0; k < cycle.size(); ++k) {
if (cycle.get(k) == j) {
ans = Math.max(ans, cycle.size() - k);
}
}
}
return ans;
}
private int topologicalSort(int[] fa) {
int n = fa.length;
int[] indeg = new int[n];
int[] dist = new int[n];
Arrays.fill(dist, 1);
for (int v : fa) {
indeg[v]++;
}
Deque<Integer> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
if (indeg[i] == 0) {
q.offer(i);
}
}
int ans = 0;
while (!q.isEmpty()) {
int i = q.pollFirst();
dist[fa[i]] = Math.max(dist[fa[i]], dist[i] + 1);
if (--indeg[fa[i]] == 0) {
q.offer(fa[i]);
}
}
for (int i = 0; i < n; ++i) {
if (i == fa[fa[i]]) {
ans += dist[i];
}
}
return ans;
}
}class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
return max(maxCycle(favorite), topologicalSort(favorite));
}
int maxCycle(vector<int>& fa) {
int n = fa.size();
vector<bool> vis(n);
int ans = 0;
for (int i = 0; i < n; ++i) {
if (vis[i]) continue;
vector<int> cycle;
int j = i;
while (!vis[j]) {
cycle.push_back(j);
vis[j] = true;
j = fa[j];
}
for (int k = 0; k < cycle.size(); ++k) {
if (cycle[k] == j) {
ans = max(ans, (int) cycle.size() - k);
break;
}
}
}
return ans;
}
int topologicalSort(vector<int>& fa) {
int n = fa.size();
vector<int> indeg(n);
vector<int> dist(n, 1);
for (int v : fa) ++indeg[v];
queue<int> q;
for (int i = 0; i < n; ++i)
if (indeg[i] == 0) q.push(i);
while (!q.empty()) {
int i = q.front();
q.pop();
dist[fa[i]] = max(dist[fa[i]], dist[i] + 1);
if (--indeg[fa[i]] == 0) q.push(fa[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i)
if (i == fa[fa[i]]) ans += dist[i];
return ans;
}
};func maximumInvitations(favorite []int) int {
a, b := maxCycle(favorite), topologicalSort(favorite)
return max(a, b)
}
func maxCycle(fa []int) int {
n := len(fa)
vis := make([]bool, n)
ans := 0
for i := range fa {
if vis[i] {
continue
}
j := i
cycle := []int{}
for !vis[j] {
cycle = append(cycle, j)
vis[j] = true
j = fa[j]
}
for k, v := range cycle {
if v == j {
ans = max(ans, len(cycle)-k)
break
}
}
}
return ans
}
func topologicalSort(fa []int) int {
n := len(fa)
indeg := make([]int, n)
dist := make([]int, n)
for i := range fa {
dist[i] = 1
}
for _, v := range fa {
indeg[v]++
}
q := []int{}
for i, v := range indeg {
if v == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
i := q[0]
q = q[1:]
dist[fa[i]] = max(dist[fa[i]], dist[i]+1)
indeg[fa[i]]--
if indeg[fa[i]] == 0 {
q = append(q, fa[i])
}
}
ans := 0
for i := range fa {
if i == fa[fa[i]] {
ans += dist[i]
}
}
return ans
}function maximumInvitations(favorite: number[]): number {
return Math.max(maxCycle(favorite), topologicalSort(favorite));
}
function maxCycle(fa: number[]): number {
const n = fa.length;
const vis: boolean[] = Array(n).fill(false);
let ans = 0;
for (let i = 0; i < n; ++i) {
if (vis[i]) {
continue;
}
const cycle: number[] = [];
let j = i;
for (; !vis[j]; j = fa[j]) {
cycle.push(j);
vis[j] = true;
}
for (let k = 0; k < cycle.length; ++k) {
if (cycle[k] === j) {
ans = Math.max(ans, cycle.length - k);
}
}
}
return ans;
}
function topologicalSort(fa: number[]): number {
const n = fa.length;
const indeg: number[] = Array(n).fill(0);
const dist: number[] = Array(n).fill(1);
for (const v of fa) {
++indeg[v];
}
const q: number[] = [];
for (let i = 0; i < n; ++i) {
if (indeg[i] === 0) {
q.push(i);
}
}
let ans = 0;
while (q.length) {
const i = q.pop()!;
dist[fa[i]] = Math.max(dist[fa[i]], dist[i] + 1);
if (--indeg[fa[i]] === 0) {
q.push(fa[i]);
}
}
for (let i = 0; i < n; ++i) {
if (i === fa[fa[i]]) {
ans += dist[i];
}
}
return ans;
}