comments

difficulty

edit_url

637. 二叉树的层平均值

题目描述

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^-5 以内的答案可以被接受。

示例 1：

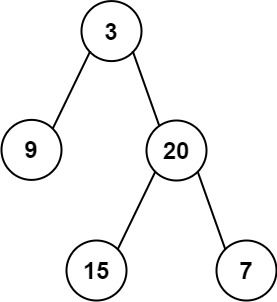
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2:

输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

提示：

树中节点数量在 [1, 10⁴] 范围内
-2³¹ <= Node.val <= 2³¹ - 1

解法

方法一：BFS

我们可以使用广度优先搜索的方法，遍历每一层的节点，计算每一层的平均值。

具体地，我们定义一个队列 $q$，初始时将根节点加入队列。每次将队列中的所有节点取出，计算这些节点的平均值，加入答案数组中，并将这些节点的子节点加入队列。重复这一过程，直到队列为空。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        q = deque([root])
        ans = []
        while q:
            s, n = 0, len(q)
            for _ in range(n):
                root = q.popleft()
                s += root.val
                if root.left:
                    q.append(root.left)
                if root.right:
                    q.append(root.right)
            ans.append(s / n)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> ans = new ArrayList<>();
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        while (!q.isEmpty()) {
            int n = q.size();
            long s = 0;
            for (int i = 0; i < n; ++i) {
                root = q.pollFirst();
                s += root.val;
                if (root.left != null) {
                    q.offer(root.left);
                }
                if (root.right != null) {
                    q.offer(root.right);
                }
            }
            ans.add(s * 1.0 / n);
        }
        return ans;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        queue<TreeNode*> q{{root}};
        vector<double> ans;
        while (!q.empty()) {
            int n = q.size();
            long long s = 0;
            for (int i = 0; i < n; ++i) {
                root = q.front();
                q.pop();
                s += root->val;
                if (root->left) {
                    q.push(root->left);
                }
                if (root->right) {
                    q.push(root->right);
                }
            }
            ans.push_back(s * 1.0 / n);
        }
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func averageOfLevels(root *TreeNode) []float64 {
	q := []*TreeNode{root}
	ans := []float64{}
	for len(q) > 0 {
		n := len(q)
		s := 0
		for i := 0; i < n; i++ {
			root = q[0]
			q = q[1:]
			s += root.Val
			if root.Left != nil {
				q = append(q, root.Left)
			}
			if root.Right != nil {
				q = append(q, root.Right)
			}
		}
		ans = append(ans, float64(s)/float64(n))
	}
	return ans
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;

impl Solution {
    pub fn average_of_levels(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<f64> {
        let mut ans = vec![];
        let mut q = VecDeque::new();
        if let Some(root_node) = root {
            q.push_back(root_node);
        }
        while !q.is_empty() {
            let n = q.len();
            let mut s: i64 = 0;
            for _ in 0..n {
                if let Some(node) = q.pop_front() {
                    let node_borrow = node.borrow();
                    s += node_borrow.val as i64;
                    if let Some(left) = node_borrow.left.clone() {
                        q.push_back(left);
                    }
                    if let Some(right) = node_borrow.right.clone() {
                        q.push_back(right);
                    }
                }
            }
            ans.push((s as f64) / (n as f64));
        }
        ans
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var averageOfLevels = function (root) {
    const q = [root];
    const ans = [];
    while (q.length) {
        const n = q.length;
        const nq = [];
        let s = 0;
        for (const { val, left, right } of q) {
            s += val;
            left && nq.push(left);
            right && nq.push(right);
        }
        ans.push(s / n);
        q.splice(0, q.length, ...nq);
    }
    return ans;
};

方法二：DFS

我们也可以使用深度优先搜索的方法，来计算每一层的平均值。

具体地，我们定义一个数组 $s$，其中 $s[i]$ 是一个二元组，表示第 $i$ 层的节点值之和以及节点个数。我们对树进行深度优先搜索，对于每一个节点，我们将节点的值加到对应的 $s[i]$ 中，并将节点个数加一。最后，对于每一个 $s[i]$，我们计算平均值，加入答案数组中。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        def dfs(root, i):
            if root is None:
                return
            if len(s) == i:
                s.append([root.val, 1])
            else:
                s[i][0] += root.val
                s[i][1] += 1
            dfs(root.left, i + 1)
            dfs(root.right, i + 1)

        s = []
        dfs(root, 0)
        return [a / b for a, b in s]

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Long> s = new ArrayList<>();
    private List<Integer> cnt = new ArrayList<>();

    public List<Double> averageOfLevels(TreeNode root) {
        dfs(root, 0);
        List<Double> ans = new ArrayList<>();
        for (int i = 0; i < s.size(); ++i) {
            ans.add(s.get(i) * 1.0 / cnt.get(i));
        }
        return ans;
    }

    private void dfs(TreeNode root, int i) {
        if (root == null) {
            return;
        }
        if (s.size() == i) {
            s.add((long) root.val);
            cnt.add(1);
        } else {
            s.set(i, s.get(i) + root.val);
            cnt.set(i, cnt.get(i) + 1);
        }
        dfs(root.left, i + 1);
        dfs(root.right, i + 1);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

using ll = long long;

class Solution {
public:
    vector<ll> s;
    vector<int> cnt;

    vector<double> averageOfLevels(TreeNode* root) {
        dfs(root, 0);
        vector<double> ans(s.size());
        for (int i = 0; i < s.size(); ++i) {
            ans[i] = (s[i] * 1.0 / cnt[i]);
        }
        return ans;
    }

    void dfs(TreeNode* root, int i) {
        if (!root) return;
        if (s.size() == i) {
            s.push_back(root->val);
            cnt.push_back(1);
        } else {
            s[i] += root->val;
            cnt[i]++;
        }
        dfs(root->left, i + 1);
        dfs(root->right, i + 1);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func averageOfLevels(root *TreeNode) []float64 {
	s := []int{}
	cnt := []int{}
	var dfs func(root *TreeNode, i int)
	dfs = func(root *TreeNode, i int) {
		if root == nil {
			return
		}
		if len(s) == i {
			s = append(s, root.Val)
			cnt = append(cnt, 1)
		} else {
			s[i] += root.Val
			cnt[i]++
		}
		dfs(root.Left, i+1)
		dfs(root.Right, i+1)
	}
	dfs(root, 0)
	ans := []float64{}
	for i, t := range s {
		ans = append(ans, float64(t)/float64(cnt[i]))
	}
	return ans
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var averageOfLevels = function (root) {
    const s = [];
    const cnt = [];
    function dfs(root, i) {
        if (!root) {
            return;
        }
        if (s.length == i) {
            s.push(root.val);
            cnt.push(1);
        } else {
            s[i] += root.val;
            cnt[i]++;
        }
        dfs(root.left, i + 1);
        dfs(root.right, i + 1);
    }
    dfs(root, 0);
    return s.map((v, i) => v / cnt[i]);
};

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

637. 二叉树的层平均值

题目描述

解法

方法一：BFS

Python3

Java

C++

Go

Rust

JavaScript

方法二：DFS

Python3

Java

C++

Go

JavaScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

637. 二叉树的层平均值

题目描述

解法

方法一：BFS

Python3

Java

C++

Go

Rust

JavaScript

方法二：DFS

Python3

Java

C++

Go

JavaScript