Skip to content

Latest commit

 

History

History
204 lines (169 loc) · 5.89 KB

README.md

File metadata and controls

204 lines (169 loc) · 5.89 KB
Raw
comments difficulty edit_url tags
true
中等
数组
动态规划
矩阵

2510. 检查是否有路径经过相同数量的 0 和 1 🔒

English Version

题目描述

给定一个 下标从 0 开始 的 m x n 的 二进制 矩阵 grid ，从坐标为 (row, col) 的元素可以向右走 (row, col+1) 或向下走 (row+1, col) 。

返回一个布尔值，表示从 (0, 0) 出发是否存在一条路径，经过 相同 数量的 0 和 1，到达终点 (m-1, n-1) 。如果存在这样的路径返回 true ，否则返回 false 。

 

示例 1 ：

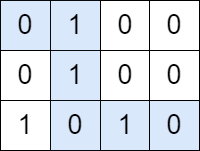
输入：grid = [[0,1,0,0],[0,1,0,0],[1,0,1,0]]
输出：true
解释：以上图中用蓝色标记的路径是一个有效的路径，因为路径上有 3 个值为 1 的单元格和 3 个值为 0 的单元格。由于存在一个有效的路径，因此返回 true 。

示例 2 ：

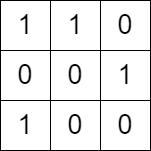
输入：grid = [[1,1,0],[0,0,1],[1,0,0]]
输出：false
解释：这个网格中没有一条路径经过相等数量的0和1。

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 100
  • grid[i][j] 不是 0 就是 1 。

解法

方法一：记忆化搜索

根据题目描述我们知道，从左上角到右下角的路径上 $0$ 的个数和 $1$ 的个数相等，个数总和为 $m + n - 1$，即 $0$ 的个数和 $1$ 的个数都为 $(m + n - 1) / 2$。

因此我们可以使用记忆化搜索，从左上角开始，向右或向下移动，直到到达右下角，判断路径上 $0$ 的个数和 $1$ 的个数是否相等即可。

时间复杂度 $O(m \times n \times (m + n))$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

Python3

class Solution:
    def isThereAPath(self, grid: List[List[int]]) -> bool:
        @cache
        def dfs(i, j, k):
            if i >= m or j >= n:
                return False
            k += grid[i][j]
            if k > s or i + j + 1 - k > s:
                return False
            if i == m - 1 and j == n - 1:
                return k == s
            return dfs(i + 1, j, k) or dfs(i, j + 1, k)

        m, n = len(grid), len(grid[0])
        s = m + n - 1
        if s & 1:
            return False
        s >>= 1
        return dfs(0, 0, 0)

Java

class Solution {
    private int s;
    private int m;
    private int n;
    private int[][] grid;
    private Boolean[][][] f;

    public boolean isThereAPath(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        s = m + n - 1;
        f = new Boolean[m][n][s];
        if (s % 2 == 1) {
            return false;
        }
        s >>= 1;
        return dfs(0, 0, 0);
    }

    private boolean dfs(int i, int j, int k) {
        if (i >= m || j >= n) {
            return false;
        }
        k += grid[i][j];
        if (f[i][j][k] != null) {
            return f[i][j][k];
        }
        if (k > s || i + j + 1 - k > s) {
            return false;
        }
        if (i == m - 1 && j == n - 1) {
            return k == s;
        }
        f[i][j][k] = dfs(i + 1, j, k) || dfs(i, j + 1, k);
        return f[i][j][k];
    }
}

C++

class Solution {
public:
    bool isThereAPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int s = m + n - 1;
        if (s & 1) return false;
        int f[m][n][s];
        s >>= 1;
        memset(f, -1, sizeof f);
        function<bool(int, int, int)> dfs = [&](int i, int j, int k) -> bool {
            if (i >= m || j >= n) return false;
            k += grid[i][j];
            if (f[i][j][k] != -1) return f[i][j][k];
            if (k > s || i + j + 1 - k > s) return false;
            if (i == m - 1 && j == n - 1) return k == s;
            f[i][j][k] = dfs(i + 1, j, k) || dfs(i, j + 1, k);
            return f[i][j][k];
        };
        return dfs(0, 0, 0);
    }
};

Go

func isThereAPath(grid [][]int) bool {
	m, n := len(grid), len(grid[0])
	s := m + n - 1
	if s%2 == 1 {
		return false
	}
	s >>= 1
	f := [100][100][200]int{}
	var dfs func(i, j, k int) bool
	dfs = func(i, j, k int) bool {
		if i >= m || j >= n {
			return false
		}
		k += grid[i][j]
		if f[i][j][k] != 0 {
			return f[i][j][k] == 1
		}
		f[i][j][k] = 2
		if k > s || i+j+1-k > s {
			return false
		}
		if i == m-1 && j == n-1 {
			return k == s
		}
		res := dfs(i+1, j, k) || dfs(i, j+1, k)
		if res {
			f[i][j][k] = 1
		}
		return res
	}
	return dfs(0, 0, 0)
}