PyHGF is a Python library written on top of JAX to create and manipulate graph neural networks that can perform belief updates through the diffusion of predictions and precision-weighted prediction errors. These networks can serve as biologically plausible computational models of cognitive functions for computational psychiatry and reinforcement learning or as a generalisation of Bayesian filtering to arbitrarily sized graphical structures for signal processing. In their most standard form, these models are a generalisation and nodalisation of the Hierarchical Gaussian Filters (HGF) for predictive coding. The library is made modular and designed to facilitate the manipulation of probabilistic networks, so the user can focus on model design. The core functions are derivable, JIT-able, and designed to interface smoothly with other libraries in the JAX ecosystem for neural networks, reinforcement learning, Bayesian inference or optimization.
The last official release can be downloaded from PIP:
pip install pyhgf
The current version under development can be installed from the master branch of the GitHub folder:
pip install “git+https://github.com/ilabcode/pyhgf.git”
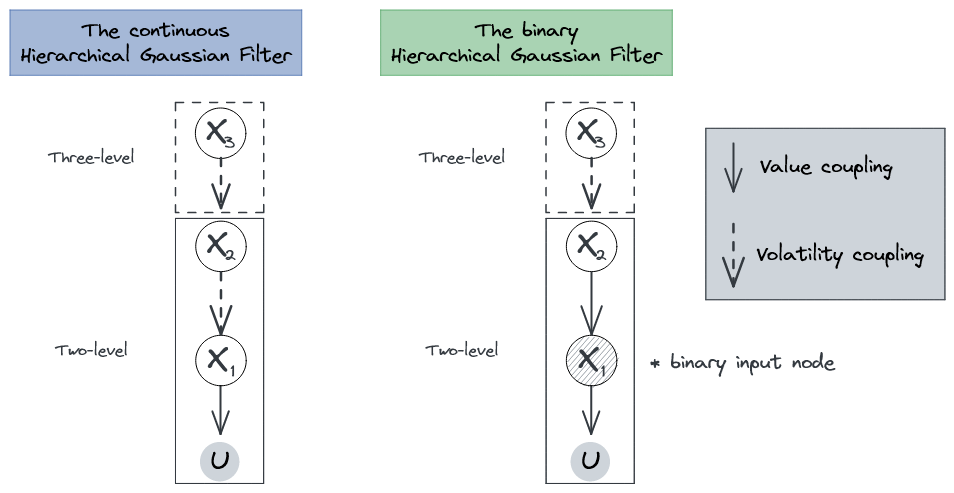
The nodalized Hierarchical Gaussian Filter consists of a network of probabilistic nodes hierarchically structured where each node can inherit its value and volatility sufficient statistics from other parent nodes. The presentation of a new observation at the lower level of the hierarchy (i.e. the input node) triggers a recursive update of the nodes' belief through the bottom-up propagation of precision-weighted prediction error.
More generally, pyhgf operates on graph neural networks that can be defined and updated through the following variables:
- The nodes' attributes (dictionary) that store each node's parameters (value, precision, learning rates, volatility coupling, ...).
- The edges (tuple) that lists, for each node, the indexes of the value and volatility parents.
- A set of update functions that operate on any of the 3 other variables, starting from a target node.
- An update sequence (tuple) that defines the order in which the update functions are called, and the target node.
Value parent and volatility parent are nodes themself. Any node can be a value and/or volatility parent for other nodes and have multiple value and/or volatility parents. A filtering structure consists of nodes embedding other nodes hierarchically. Nodes are parametrized by their sufficient statistic and parents. The transformations between nodes can be linear, non-linear, or any function (thus a generalization of the HGF).
The resulting probabilistic network operates as a filter toward new observation. If a decision function (taking the whole model as a parameter) is also defined, behaviours can be triggered accordingly. By comparing those behaviours with actual outcomes, a surprise function can be optimized over the range of parameters of interest.
You can find a deeper introduction to how to create and manipulate networks under the following link:
The Hierarchical Gaussian Filter for binary and continuous inputs as it was described in Mathys et al. (2011, 2014), and later implemented in the Matlab Tapas toolbox (Frässle et al. 2021), can be seen as a special case of this node structure such as:
The pyhgf package includes pre-implemented standard HGF models that can be used together with other neural network libraries of Bayesian inference tools. It is also possible for the user to build custom network structures that would match specific needs.
You can find a deeper introduction on how does the HGF works under the following link:
Here we demonstrate how to fit a two-level binary Hierarchical Gaussian filter. The input time series are the binary outcomes from Iglesias et al. (2013).
from pyhgf.model import HGF
from pyhgf import load_data
# Load time series example data
u, _ = load_data("binary")
# This is where we define all the model parameters - You can control the value of
# different variables at different levels using the corresponding dictionary.
hgf = HGF(
n_levels=2,
model_type="binary",
initial_mean={"1": .0, "2": .5},
initial_precision={"1": .0, "2": 1e4},
tonic_volatility={"2": -3.0},
)
# add new observations
hgf.input_data(input_data=u)
# compute the model's surprise (-log(p))
surprise = hgf.surprise()
print(f"Model's surprise = {surprise}")
# visualization of the belief trajectories
hgf.plot_trajectories();Creating a binary Hierarchical Gaussian Filter with 2 levels.
... Create the update sequence from the network structure.
... Create the belief propagation function.
... Cache the belief propagation function.
Adding 320 new observations.
Model's surprise = 203.6395263671875
This implementation of the Hierarchical Gaussian Filter was largely inspired by the original Matlab version. A Julia implementation of the generalized, nodalised and multilevel HGF is also available here.
- Mathys, C. (2011). A Bayesian foundation for individual learning under uncertainty. In Frontiers in Human Neuroscience (Vol. 5). Frontiers Media SA. https://doi.org/10.3389/fnhum.2011.00039
- Mathys, C. D., Lomakina, E. I., Daunizeau, J., Iglesias, S., Brodersen, K. H., Friston, K. J., & Stephan, K. E. (2014). Uncertainty in perception and the hierarchical Gaussian filter. Frontiers in Human Neuroscience, 8. https://doi.org/10.3389/fnhum.2014.00825
- Weber, L. A., Waade, P. T., Legrand, N., Møller, A. H., Stephan, K. E., & Mathys, C. (2023). The generalized Hierarchical Gaussian Filter (Version 1). arXiv. https://doi.org/10.48550/ARXIV.2305.10937
- Frässle, S., Aponte, E. A., Bollmann, S., Brodersen, K. H., Do, C. T., Harrison, O. K., Harrison, S. J., Heinzle, J., Iglesias, S., Kasper, L., Lomakina, E. I., Mathys, C., Müller-Schrader, M., Pereira, I., Petzschner, F. H., Raman, S., Schöbi, D., Toussaint, B., Weber, L. A., … Stephan, K. E. (2021). TAPAS: An Open-Source Software Package for Translational Neuromodeling and Computational Psychiatry. In Frontiers in Psychiatry (Vol. 12). Frontiers Media SA. https://doi.org/10.3389/fpsyt.2021.680811