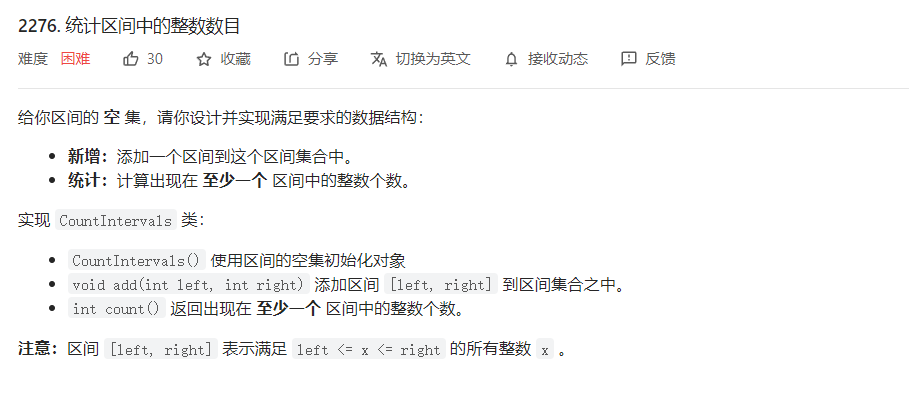
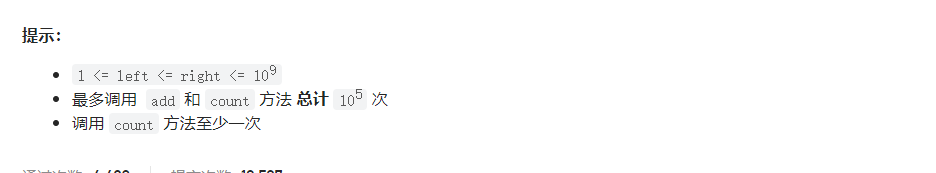我们希望提供一种数据结构,能够在线的维护由整数组成的闭区间的并集,并且获得维护的闭区间中的整数个数。
珂朵莉树的思想可以很好的解决这个问题,至于为啥叫珂朵莉树,是因为codeforces上最早的这类型问题的最优解法的贡献者顶着一个珂朵莉的头像。
它的主要思想是通过有序集合set来维护这些区间,set<pair<int, int>>中存一系列不相交的[右端点, 左端点],每次插入新的集合[L, R]的时候,通过set的lower_bound(L - 1)成员函数找到第一个右端点大于等于L - 1的区间(L - 1是为了合并如[3, 4] [4, 5]这样的区间),然后开始合并,L = L与当前迭代器指向的区间的左端点的较小值,R = R与当前迭代器指向的区间的右端点的较大值,然后再区间中删除当前迭代器指向的区间,记得同时维护区间中的整数个数,直到迭代器指向的区间的左端点大于R + 1为止跳出循环。最后,让区间中的整数个数增加R - L + 1,并且插入[R, L]区间。
class CountIntervals {
public:
CountIntervals() {}
void add(int left, int right)
{
int l = left, r = right;
auto it = tree.lower_bound({l - 1, -2e9});
while (it != tree.end())
{
if (it->second > r + 1) break;
l = min(l, it->second);
r = max(r, it->first);
cnt -= it->first - it->second + 1;
it = tree.erase(it);
}
cnt += r - l + 1;
tree.insert({r, l});
}
int count()
{
return cnt;
}
private:
typedef pair<int, int> pii;
set<pii> tree;
int cnt = 0;
};