| title | date | tags | ||
|---|---|---|---|---|
统计树中的合法路径数目---LeetCode2867(树形dp) |
2023-09-27 10:17:04 -0700 |
|
日期: 2023-09-27
给你一棵 n 个节点的无向树,节点编号为 1 到 n 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。
请你返回树中的 合法路径数目 。
如果在节点 a 到节点 b 之间 恰好有一个 节点的编号是质数,那么我们称路径 (a, b) 是 合法的 。
注意:
- 路径
(a, b)指的是一条从节点a开始到节点b结束的一个节点序列,序列中的节点 互不相同 ,且相邻节点之间在树上有一条边。 - 路径
(a, b)和路径(b, a)视为 同一条 路径,且只计入答案 一次 。
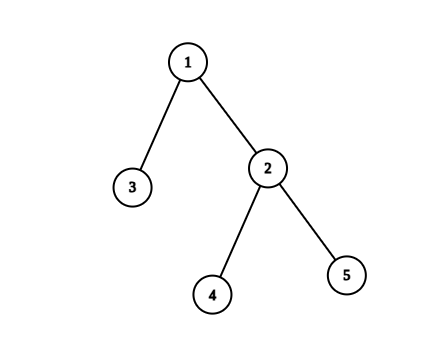
输入:n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
输出:4
解释:恰好有一个质数编号的节点路径有:
- (1, 2) 因为路径 1 到 2 只包含一个质数 2 。
- (1, 3) 因为路径 1 到 3 只包含一个质数 3 。
- (1, 4) 因为路径 1 到 4 只包含一个质数 2 。
- (2, 4) 因为路径 2 到 4 只包含一个质数 2 。
只有 4 条合法路径。
我也不知道这种做法是不是叫做树形dp,反正感觉很怪,而且也很难想到。
因为要求一条路径上只能有一个质数,所以这道题就使用枚举质数节点的方式来做。
当枚举到一个节点为质数时,该节点会把这棵树划分为不同的连通块,对于一个连通块,我们使用dfs的方式来计算这个连通块里面非质数的数量。
假如最后计算出来对于一个质数,有三个连通块,他们分别的非质数数量为 1,2,3
那么其实更新到答案里面的数就是:
1 + 2 + 3 + 1 * 5 + 2 * 4 + 3 * 3
分别表示自身以及选择一个然后与其他的组合的情况。
一些注意点:
- 这道题使用了一个cnt来避免重复计算,类似于备忘录
- dfs的时候要注意避免死循环,也就是加个fa来判断一下。
- 这道题一个比较有意思的点是使用了一个nodes数组来存连通块里面的所有点,使用这种方式既能够记录下连通块里面所有的元素,又可以使用.size()来拿到连通块的大小,我觉得这里很巧妙。
代码:
class Solution {
public:
int isPrime(int num){
if(num==2)
return 1;
if(num%2==0 || num<2)
return 0;
else{
for(int i=3;i*i<=num;i+=2){
if(num%i==0){
return 0;
}
}
return 1;
}
}
unordered_map<int, vector<int>> e;
vector<int> nodes;
unordered_map<int,int> size;
// dfs统计从x开始的连通块里面非质数的数量
void dfs(int x, int fa){
if(isPrime(x)) return;
nodes.push_back(x);
for(int next:e[x]){
if(next == fa) continue;
dfs(next,x);
}
}
long long countPaths(int n, vector<vector<int>>& edges) {
for(auto& x:edges){
e[x[0]].push_back(x[1]);
e[x[1]].push_back(x[0]);
}
long long ans = 0 ;
for(int i=1; i<=n; i++){
if(isPrime(i)){
vector<int> tmp;
long long sum = 0;
for(int x:e[i]){
if(isPrime(x)) continue;
if(size.count(x) == 0){
// 计算size
nodes.clear();
dfs(x, -1);
for(int no:nodes){
size[no] = nodes.size();
}
}
tmp.push_back(size[x]);
sum += size[x];
}
long long newAdd = 0;
for(int x:tmp){
newAdd += (sum - x) * x;
}
ans += newAdd/2;
ans += sum;
}
}
return ans;
}
};