Skip to content

Latest commit

 

History

History
302 lines (242 loc) · 12.1 KB

2.神经网络基础.md

File metadata and controls

302 lines (242 loc) · 12.1 KB
Raw

2.1 多层感知机和感知机的区别是什么，为什么会有这样的区别？

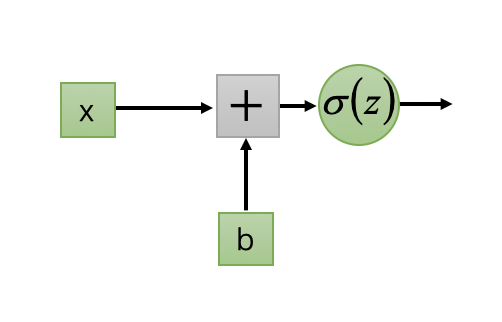
感知机是只有一个神经元的单层神经网络。（摘录自课本 Page 17）

多层感知机是20世纪八九十年代常用的一种两层的神经网络。（摘录自课本 Page 19）

首先，感知机和多层感知机都可以接受若干个输入，但感知机只能有一个输出，多层感知机可以有多个输出。

此外，相比感知机而言，多层感知机可以解决输入非线性可分的问题。

2.2 假设有一个只有一个隐层的多层感知机，其输入、隐层、输出层的神经元个数分别为33、512、10，那么这个多层感知机中总共有多少个参数是可以被训练的？

确定weight的个数： $$ weights = 33 * 512 +512*10= 22016 $$ 确定bias的个数： $$ biases =1+1=2 $$ 这样，总共可以被训练的参数是22018个。

2.3 反向传播中，神经元的梯度是如何计算的？权重是如何更新的？

基于梯度下降法的神经网络反向传播过程首先需要根据应用场景定义合适损失函数（loss function），常用的损失函数有均方差损失函数和交叉熵损失函数。确定了损失函数之后，把网络的实际输出与期盼输出结合损失函数计算loss，如果loss不符合预期，则对loss分别求权重和偏置的偏导数，然后沿梯度下降方向更新权重及偏置参数。

不引入惩罚项的权重更新公式如下： $$ w \gets w-\eta(\triangledown_wL(w;x,y)) $$

2.4 请在同一个坐标系内画出五种不同的激活函数图像，并比较它们的取值范围。

仓库地址：https://github.com/LeiWang1999/AICS-Course/blob/master/Code/2.4.activationplot.py

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1.0/(1.0+np.exp(-1.0 * x))

def tanh(x):
    return (np.exp(x)-np.exp(-1.0 * x))/(np.exp(x)+np.exp(-1.0 * x))

def ReLU(x):
    return np.maximum(0, x)

def PReLU(x, a=-0.01):
    return np.maximum(a*x, x)

def ELU(x, a=-0.01):
    y = np.zeros_like(x)
    for index, each in enumerate(x):
        y[index] = each if each>0 else a*(np.exp(each)-1.0)
    return y

x=np.linspace(-10,10,256,endpoint=True)#-π to+π的256个值
y_sigmoid = sigmoid(x)
y_tanh = tanh(x)
y_ReLU = ReLU(x)
y_PReLU = PReLU(x)
y_ELU = ELU(x)
plt.grid() # 生成网格
plt.plot(x, y_sigmoid, label='sigmoid')
plt.plot(x, y_tanh, label='tanh')
plt.plot(x, y_ReLU, label='ReLU')
plt.plot(x, y_PReLU, label='PReLU')
plt.plot(x, y_ELU, label='ELU')
plt.legend(['sigmoid','tanh', 'ReLU', 'PReLU', 'ELU'])
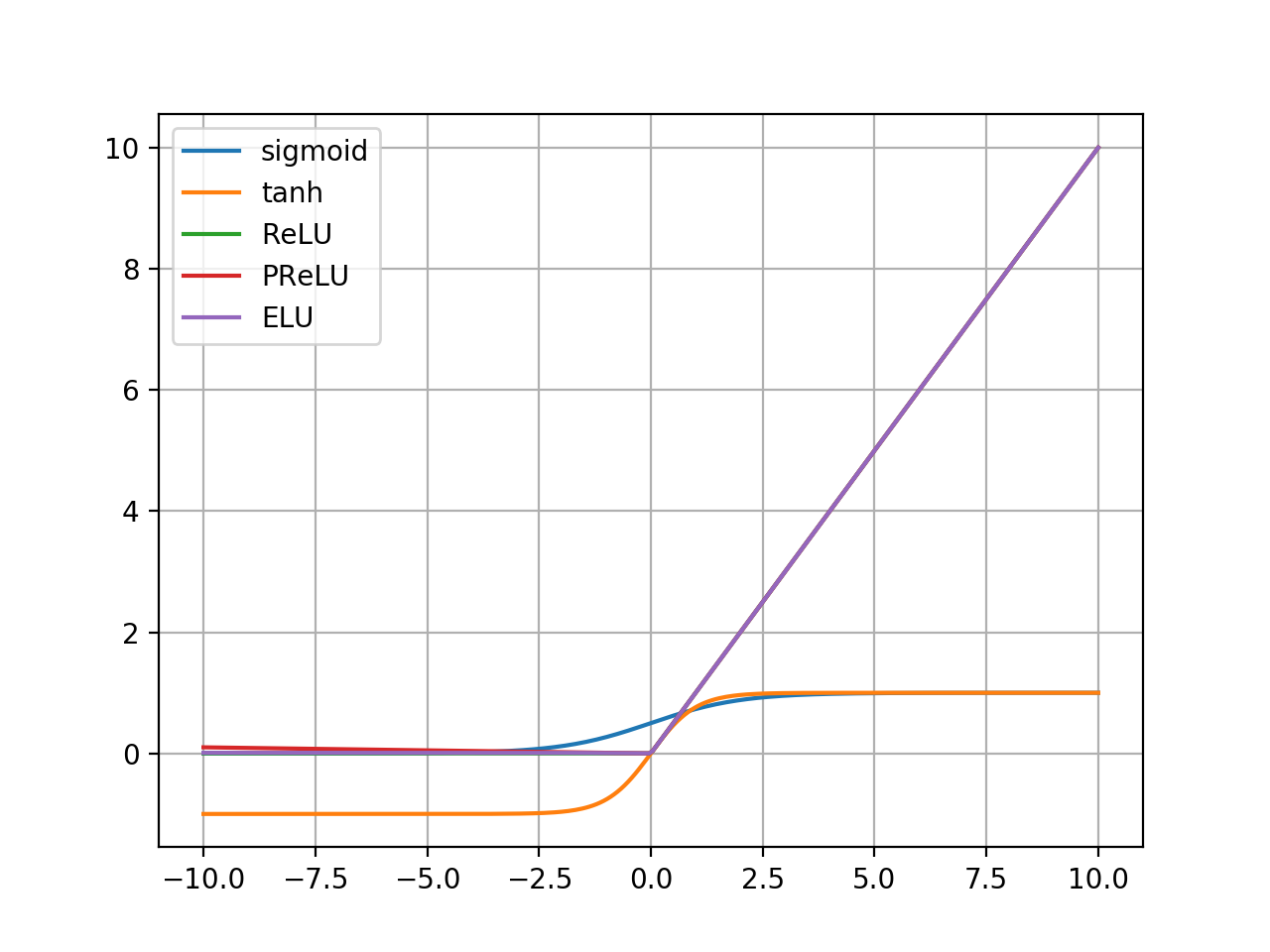
plt.show()

绘图结果如下：

Figure_1

对输入取区间[-10, 10],a取-0.01:比较取值范围：

Function Minimum Maximum
sigmoid 0 1
tanh -1 1
ReLU 0 10
PReLU -0.1 10
ELU 0.00038 10

2.5 请简述三种避免过拟合问题的方法

  1. 在损失函数中增加惩罚项，常用的方法有L1正则化和L2正则化，L1正则化可以使训练出来的weight更接近于0，L2正则化可以使全中国weight的绝对值变小。
  2. 稀疏化，在训练的时候将神经网络中的很多权重或神经元设置成0，也是通过增加一些惩罚项来实现的。
  3. Bagging集成学习，应对一个问题时训练几个不同的网络，最后取结果的加权，减少神经网络的识别误差
  4. Dropout会在训练的时候随机删除一些节点，往往会起到意想不到的结果，一般来说我们设置输入节点的采样率为0.8，隐层节点的采样率为0.5。在推理阶段，我们再将对应的节点输出乘以采样率，即训练的时候使用Dropout，但是推理的时候会使用未经裁剪的整个网络。

2.6 sigmoid激活函数的极限是0和1，请给出它的导数形式并求出其在原点的值

sigmoid函数如下： $$ sigmoid(x) = \frac{1}{1+e^{-x}} $$ 求sigmoid函数的导数: $$ \frac{\mathrm{d}sigmoid(x)}{x} = \frac{e^{-x}}{(1+e^{-x})^2}=\frac{1}{e^{-x}+e^x+2} $$ 在原点处的值为: $$ \frac{1}{1+1+2}=0.25 $$

2.7 假设激活函数的表达式为$\phi(v)=\frac{v}{\sqrt{1+v^2}}$，请给出它的导数形式并求出其在原点的取值

$$ \frac{\mathrm{d}\phi(v)}{\mathrm{d}v}=\frac{\mathrm{d}v*(1+v^2)^{-1/2}}{\mathrm{d}v}=\frac{\mathrm{d}(1+v^2)(1+v^2)^{-3/2}+\mathrm{d}-v^2(1+v^2)^{-3/2}}{\mathrm{d}v}=\frac{1}{(1+v^2)^{3/2}} $$

当在原点处时，该激活函数的导数取值为1。

2.8 假设基本采用表2.1中的符号，一个经过训练的有两个隐层的MLP如何决定各个输出神经元的标签？预测过程中，当前输入的样本的标签如何决定？

题目没有给出，两个隐藏层的神经元个数是多少个，我们可以假设输入矩阵为x，输入层和第一层隐层的权重为w1，第一层隐层和第二层隐层的权重为w2.输出为y，则有: $$ temp=w_1^Tx \\ y = w_2^Ttemp $$ 输出样本的标签由输出y的最大值的下标决定。

2.9 一种更新权重的方法是引入动量项，公式如下，动量a的取值范围通常为[0, 1]，这样对于权重更新有什么影响？如果取值范围是[-1,0]呢？

$$ \triangle w(n) = a\triangle w(n-1)+a^2\triangle w(n-2)+... $$

当a为[0,1]时，动量项表现为惩罚项，每一次求梯度的时候都会考虑到之前几步更新权重的的动量，并且距离越近影响越大，梯度更新的曲线会越平滑，并且因为考虑到动量，就有可能突破local minimal，找到global minimal。具体的知识可以以momentum为keyword搜索相关资料。

当a为[-1,0]时，动量项表现为奖励项，这样梯度的收敛曲线应该会更陡峭，至于有啥用途想不到。

2.10 反向传播中，采用不同的激活函数对于梯度的计算有什么不同？请设计一个新的激活函数并给出神经元的梯度计算公式。

梯度的计算需要求目标函数关于权重和偏置的偏导数，激活函数不同会导致偏导数不同，进而影响梯度的计算。

设计一个新的激活函数： $$ \delta(z) = e^z $$ 对一个简单的神经元：

sensor

则有 $$ y = \delta(wx+b)=e^{wx+b} $$ 选择目标函数为均方误差（mean-square error, MSE）： $$ Loss=(\check y - y)^2 = (\check y - e^{w*x+b})^2 $$ 神经元的梯度计算公式: $$ \triangledown_w=\frac{\partial Loss}{\partial w}=-2xe^{wx+b}(\check y - e^{wx+b}) \\ \triangledown_b=\frac{\partial Loss}{\partial b}=2e^{wx+b}(\check y - e^{wx+b}) $$

2.11 请设计一个多层感知机实现4位全加器的功能，即两个4比特输入得到一个4比特输出以及1比特进位。请自行构建训练集、测试集，完成训练及测试。

Github Code Link：https://github.com/LeiWang1999/AICS-Course/tree/master/Code/2.11.fulladder.pytorch

框架：Pytorch

网络结构：简单的MLP、两个隐层layer、各20个node、激活函数使用的是Relu。

class MLP(nn.Module):
    def __init__(self, input_dim, hidden_1, hidden_2, output_dim):
        super(MLP,self).__init__()
        self.layer1 = nn.Sequential(nn.Linear(input_dim, hidden_1), nn.ReLU(True))
        self.layer2 = nn.Sequential(nn.Linear(hidden_1, hidden_2), nn.ReLU(True))
        self.layer3 = nn.Sequential(nn.Linear(hidden_2, output_dim))

    def forward(self,x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x

数据集构建：

  1. 使用python实现二进制全加器(binary_adder.py)、然后遍历输出构建数据集
  2. 对数据集做了shuffle，再分出训练集和测试集、这样提取的特征更准确

200个epoch可以达到100%的准确率：

[epoch 194] train_loss: 0.920  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 195] train_loss: 0.929  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 196] train_loss: 0.979  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 197] train_loss: 1.004  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0020
 time.perf_counter()-t1
[epoch 198] train_loss: 0.995  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0020
 time.perf_counter()-t1
[epoch 199] train_loss: 0.927  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0010
 time.perf_counter()-t1
[epoch 200] train_loss: 0.979  test_accuracy: 1.000
Finished Training

2.12 在不使用编程框架的前提下，重新实现解决习题2.11的代码。

Github Code Link:https://github.com/LeiWang1999/AICS-Course/tree/master/Code/2.12.fulladder.cpp

int main(){
    // generate test data
    vector<vector<bool>> batch_input;
    vector<vector<bool>> batch_output;
    vector<vector<bool>> train_input;
    vector<vector<bool>> train_output;
    vector<vector<bool>> test_input;
    vector<vector<bool>> test_output;
    data_gen(batch_input, batch_output, true);
    data_split(batch_input, batch_output,
            train_input,train_output,
            test_input, test_output,
            0.7
            );
    // init MLP
    int num_layers = 4;
    int num_Neurons[] = {9, 20, 20, 5};
    int epochs = 200;
    MLP mlp(num_layers, num_Neurons);
    for(int epoch = 1; epoch <= epochs; epoch++){
        cout << "Current Epoch : " << epoch << " Batch Size : " << train_input.size() ;
        for (int i = 0; i < train_input.size(); ++i) {
            double* output = NULL;
            double target[num_Neurons[num_layers - 1]] ;
            mlp.input(train_input[i]);
            mlp.forward();
            output = mlp.get_output();
            for (int j = 0; j < num_Neurons[num_layers-1]; ++j) {
                target[j] = train_output[i][j];
            }
            mlp.backward(output, target);
        }
        int acc = 0;
        cout << " training loss : " << mlp.get_loss() << " outputBatchSize : " << test_input.size();
        for (int i = 0; i < test_input.size(); ++i) {
            double* output = NULL;
            mlp.input(test_input[i]);
            mlp.forward();
            output = mlp.get_output();
            // loop neurons
            int j;
            for (j = 0; j < num_Neurons[num_layers-1]; ++j) {
                if ((output[j]<0.5 && test_output[i][j] == 0) || (output[j] >= 0.5 && test_output[i][j] == 1))
                    continue;
                else
                    break;
            }
            if(j == num_Neurons[num_layers-1]){
                acc++;
            }
        }
        cout << " acc : " << 1.0 * acc / test_input.size() << endl;
    }
//    data_gen_test();
//    mlp_test();

    return 0;
}

和Pytorch的网络结构基本相同，不同的是激活函数使用的是Sigmoid、而Pytorch里使用的是Relu。

运行结果：

Current Epoch : 938 Batch Size : 358 training loss : 2.74758e-07 outputBatchSize : 154 acc : 0.616883
Current Epoch : 939 Batch Size : 358 training loss : 3.31897e-07 outputBatchSize : 154 acc : 0.668831
Current Epoch : 940 Batch Size : 358 training loss : 4.30856e-07 outputBatchSize : 154 acc : 0.688312
Current Epoch : 941 Batch Size : 358 training loss : 6.82454e-08 outputBatchSize : 154 acc : 0.668831
Current Epoch : 942 Batch Size : 358 training loss : 2.97463e-07 outputBatchSize : 154 acc : 0.714286
Current Epoch : 943 Batch Size : 358 training loss : 1.849e-07 outputBatchSize : 154 acc : 0.714286
Current Epoch : 944 Batch Size : 358 training loss : 1.77274e-07 outputBatchSize : 154 acc : 0.707792
Current Epoch : 945 Batch Size : 358 training loss : 3.79138e-07 outputBatchSize : 154 acc : 0.707792
Current Epoch : 946 Batch Size : 358 training loss : 7.08133e-08 outputBatchSize : 154 acc : 0.701299