This repo holds materials for our Splash 2017 class on Z3.
Z3 is a powerful theorem prover developed by Microsoft Research. Essentially, you can give Z3 a bunch of equations or constraints expressed in terms of variables, and it will do its best to find a solution that satisfies the constraints. Z3 is an example of an SMT Solver. There's a rich theory underlying how to write good SMT solvers, but we're not concerned with any of that in this class. We'll just be using Z3 as a tool in order to break some cryptography.
- Once you're logged in, double-click and install Anaconda3 on the Desktop
- While that's installing, navigate to https://github.com/TechSecCTF/z3_splash_class/ in a browser, and click the green "Clone or download" button.
- Then click "Download Zip", then click the "Save" button on the prompt at the bottom of your screen. Once it's done downloading, click "Open".
- Right-click on the big folder icon on the right, and click "Extract All"
- Set it to extract to
C:\Users\espuser. - By now, Anaconda3 should have finished installing. Once it's done, click the Windows icon on the bottom-left corner of the screen and click "Anaconda Prompt"
- Finally, wait for the prompt to load and then type
jupyter notebook - Copy the url that it gives you and paste it into your browser.
- Double click on
z3_splash_class. You should be all set.
You may also be interested in installing Z3 in a different environment. We have provided an install.sh script which should install Z3 successfully OS X or Linux. (You'll need root access). If you want to run the jupyter notebooks, you'll need to download and install jupyter. You can then get rid all the path nonsense at the top of the python source code and simply include from z3 import *.
Further installation instructions can be found here.
This image was floating around Facebook some time ago, with the caption "ONLY FOR GENiUS". Let's find the solution using Z3.
Check out examples/only_for_genius.py, reproduced below:
from Z3 import *
circle, square, triangle = Ints('circle square triangle')
s = Solver()
s.add(circle + circle == 10)
s.add(circle * square + square == 12)
s.add(circle * square - triangle * circle == circle)
print s.check()
print s.model()Let's go through it line by line:
- All of our Z3 programs will start with the line
from Z3 import *. This imports all the Z3 python bindings. - Next, we declare three integer variables,
circle,squareandtriangle. - Then, we instantiate a new solver
sand we add our three constraints. - Finally, we call the function
s.check(). In any Z3 program, this function is doing all of the heavy lifting. It checks if a solution exists given our constraints and returnssatif yes, andunsatif no. - Once we've verified that there is at least one solution, we can get Z3 to print it for us by asking it for its model.
When we run the program we see:
sat
[triangle = 1, square = 2, circle = 5]
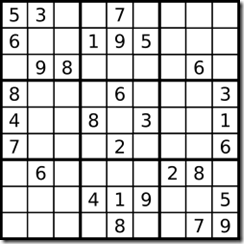
Let's get warmed up with a relatively easy example — Sudoku.
Sudoku is just a system of equations, and it's simple for Z3 to solve.
We can do this solely with the Z3 Int and Distinct types, plus some basic operators And and <=.
Check out exercises/sudoku.ipynb. Your task is to add the Z3 constraints for the individual cells, columns, and subsquares. (To get you started, we've given you the row constraints). Remember to enforce that the entries are all numbers from 1 to 9.
In computer science, a hash function is a function that takes in a string of characters (or any object really), and produces a fixed-size number (the "hash") that corresponds to that string. Importantly, the hashes of two related strings should be different. Hash functions are useful for all sorts of things in computer science (like hashtables). Cryptographic hash functions are a special type of hash function which also satisfies a number of properties, one of the most important of which is that given the hash of a string, it should be difficult to reconstruct the string.
One area where hash functions are very useful are in password checking. When a user registers with a site, they specify a password. Suppose that the webiste records the password in their database. Later when the user logs in, they enter that password and the website checks that it matches the password in their database. But now, if the website's database gets leaked, every user's account is compromised.
Suppose instead the website computes a hash of the password when a user registers and stores the hash in their database instead of the password itself. Then, whenever the user logs in, the website can just compute the hash of whatever password is entered and check the hash against whatever is stored in their database. If the database leaks (and the hash is cryptographically secure, and the passwords themselves are sufficiently complex) it should be difficult to easily reverse the hashes and compromise the user accounts.
The problem is, many people frequently use non-cryptographically secure hash functions for password-checking. In this example, we'll reverse the hash for a website using the same hash function that Java uses for its hash tables. Check out examples/java_hash.ipynb and examples/java_hash.html.
SPECK is a lightweight block cipher developed by the NSA and published in 2013.
It consists of 3 basic operations done on 64-bit numbers:
The XOR operation is very common in cryptography. It's 0 if the two input bits are the same and 1 if the two input bits are different. When applied to 64-bit numbers, the XOR is computed bit-by-bit:
a = 0b10001111100010001 = 73489
b = 0b00111001001111000 = 29304
c = 0b10110110101101001 = 93545 <--- a XOR b
In python, the XOR operation is represented by the caret symbol (^)
a = 73489
b = 29304
assert a ^ b == 93545This is standard grade-school addition. The one thing to note is that if the resulting sum is greater than 64-bits, it "overflows" and we only consider the lower 64 bits.
In a bit rotation, you literally rotate the bits of the number to the right or left by the amount specified by the operation.
Here is an example of a 3 bit right rotation:
a = 0b10001111100010001 = 73489
b = 0b00110001111100010 = 25570 <-- a >>> 3
Python doesn't have a native operation for bit rotation, but the following functions will do it for us:
MASK = (1 << 64) - 1
# Rotate 64 bit integer x right by r
def ror(x, r):
return ((x >> r) | (x << (64 - r))) & MASK
# Rotate 64 bit integer x left by r
def rol(x, r):
return ((x << r) | (x >> (64 - r))) & MASKSPECK makes heavy use of the following function r, which takes in three 64-bit numbers and modifies the first two numbers based on the third:
# SPECK round function; x, y, and k are all 64 bits
def r(x, y, k):
x = ror(x, 8)
x += y
x ^= k
y = rol(y, 3)
y ^= x
return x, ySPECK (or at least the version we're interested in) operates on 128-bit plaintext blocks. This block is immediately split into two 64-bit blocks, x and y. SPECK's key is also 128 bits long and is also split up into two 64-bit blocks, a and b.
In each round of SPECK, we use apply the r function to our plaintext (x and y) using b as the third argument. Then we modify our keys by applying the r function to our key (a and b) using the round number as the third argument.
SPECK normally includes 32 rounds. Our variant, 3SPECK, (that Z3 is able to break in a reasonable amount of time) uses only 3 rounds.
Check out exercises/speck.ipynb. We've implemented the SPECK cipher for you and provided you with a plaintext / ciphertext pair which uses some unknown key. Your task is to implemented the Z3 versions of 3SPECK's encrypt and round functions in order to derive the key. Once you have the key, we'll use it to try to decrypt a new ciphertext.
For this problem, the correct datatype to use are (64 bit) BitVecs, which act like Ints in many ways but support useful operations like RotateRight and RotateLeft. They also have the nice property that if you add two BitVecs that overflow, the resulting BitVec will only keep track of the last 64 bits.
There are many cases when writing programs that you'd want to have access to a random number generator. Psuedorandom number generators, or PRNGs for short, take a seed (some initial random value) and use that seed to produce an infinite stream of random-looking bytes. In contrast, true random number generators, or TRNGS, produce their randomness from environmental factors like radio noise or the weather or random keystrokes. The problem with TRNGs is that they are very slow. In practice PRNGs are usually enough.
There is a special class of PRNGs called cryptographically-secure psuedorandom number generators, or CSPRNGs. The basic property that these generators satisfy is that even if you get access to the first N random values that it generates (but not the seed), you can't predict anything about the next N values it will generate. You can't use Z3 to break CSPRNGs (if you could, that means something has gone really really wrong with its design), but you can absolutely use Z3 to break non-cryptographically secure PRNGs. And the thing is, people misuse PSRNGs all the time.
There's a PRNG called xorshift128+ (it roughly stands for "XOR, Shift, 128-bits, Plus"), which is the RNG that Chrome and Firefox use for their Javascript engines. It's very fast, but it's also not cryptographically secure. Given a number of its outputs, we can clone the state of the PRNG and exactly predict the rest of the numbers it will generate. In this exercise we'll clone xorrayhul64+ (a home-brewed variant of the real thing) using Z3 and then use our clone to win a Roulette wheel game.
Check out exercises/xorrayhul64p-rng.ipynb and exercises/roulette.html.
Hints:
- The website computes the numbers it generates modulo 37 to select a random place on the wheel, but if you check the javascript console log, you can see the raw numbers it generates.
- This PRNG uses left and right bit shifts, which are similar to left and right bit rotations, except the bits that fall off the edge don't get rotated around to the other end.
- There is a difference between a logical right shift and an arithmetic right shift. The former is represented in Z3 using the function
LShRwhich takes two arguments: the bit vector to be shifted and the amount to shift by. The latter is represented with the standard python operator>>. You'll need to user the former. - There is no difference between a logical and arithmetic left shift operator, so you should just use
<<. Read why here.
- Quick introduction into SAT/SMT solvers and symbolic execution - A very good, if lengthy, book on Z3
- Hacking the Javascript Lottery - Cloning Chrome's PRNG to win a javascript game
- Z3 API - https://z3prover.github.io/api/html/z3.html