Présenté par Daehli Nadeau-Otis
Les textures pour les sphères ont été ajoutées avec 2 manières différentes. La texture pour le soleil a été ajoutée avec le vertexShaders et le fragmentShader. Les textures ont été trouvées sur internet.
Le VertexShader du soleil est présenté comme ceci.
varying vec3 worldPosition;
varying vec2 vUv;
void main()
{
vec4 worldPos = modelMatrix * vec4(position, 1.0);
gl_Position = projectionMatrix * viewMatrix * worldPos;
worldPosition = worldPos.xyz;
vUv = uv;
}Ensuite le FragmentShader du soleil.
varying vec3 worldPosition;
varying vec2 vUv;
uniform sampler2D sunmap; //déclaration de l'uniform de texture. Sa valeur sera attribuée depuis le code javascript.
void main()
{
vec4 color = texture2D(sunmap, vUv);
gl_FragColor = vec4(color.rgb, 1.0);
}Étant donné que le soleil est une sphère brillante. On applique simplement la texture dessus. Il va apparaitre comme s’il était une lumière.
La texture appliquée au soleil est une image png.
La texture va être collée à la sphère. Le Soleil est maintenant créé.
Dans le shader, il n'y a pas de formule mathématique pour interprété la luminosité du soleil.
Pour interpréter la texture et l'effet de luminosité sur les autres sphères. Le THREE.MeshPhongMaterial a été très utile. Il permet d'éviter de coder le vertexShader et le fragmentShader. À des fins de démonstration, je vais implémenter le vertexShader et le fragmentShader.
Le vertexShader consiste à manipuler les vertices de la sphère.
var jupiterVertexShader =`uniform vec3 lightPosition;
varying vec2 vUv;
varying vec3 lightDir;
varying vec3 eyeDir;
varying vec3 normalV;
void main()
{
vec4 worldPos = modelMatrix * vec4(position, 1.0);
lightDir = lightPosition - worldPos.xyz;
eyeDir = cameraPosition - worldPos.xyz;
gl_Position = projectionMatrix * viewMatrix * worldPos;
normalV = normal;
vUv = uv;
}`Ensuite, on envoie la position des vertices au fragmentShader pour y appliquer la texture et la formule de réflexion de la lumière sur les sphéres.
var jupiterFragmentShader = `varying vec3 worldPosition;
varying vec2 vUv;
varying vec3 lightDir;
varying vec3 eyeDir;
varying vec3 normalV;
uniform sampler2D jupitermap;
uniform vec4 lightColor;
uniform float lightShininess;
void main()
{
vec3 N = normalize(normalV);
vec3 L = normalize(lightDir);
vec4 texture = texture2D(jupitermap,vUv);
float l = clamp(dot(N,L),0.0,1.0);
vec4 color = l * (lightColor*texture);
vec3 E = normalize(eyeDir);
vec3 R = -L - 2.0 * dot(-L,N)*N;
float specular = pow(max(dot(R,N),0.0),lightShininess);
color += lightColor * specular;
gl_FragColor = vec4(color.rgb, 1.0);
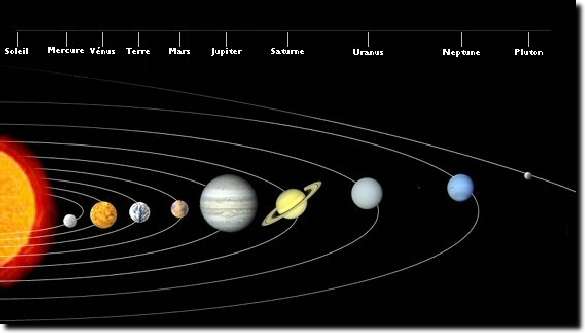
}`Dans le système solaire, toutes les planètes y sont présentes (même pluton). Les planètes sont organisées de la façon suivante.
Les planètes ne sont pas à l'échelle ni les distances. Par contre, l'axe des planètes est respecté1.
// Inclinaison des planètes
earth.rotation.z = 23.439281 * Math.PI / 180;
moon.rotation.z = 23.439281 * Math.PI / 180;
mercury.rotation.z = 0.01 * Math.PI / 180;
venus.rotation.z = 177.3 * Math.PI / 180;
mars.rotation.z = 25.19 * Math.PI / 180;
jupiter.rotation.z = 3.13 * Math.PI / 180;
saturn.rotation.z = 26.73 * Math.PI / 180;
saturn.rotation.z = 97.77 * Math.PI / 180;
saturn.rotation.z = 28.32 * Math.PI / 180;Chaque planète orbite autour du soleil. Pour résoudre le problème d'orbite dans three.js, il a fallu créer des objets groupes. Il faut encapsuler les planètes et les orbites dans l'espace autour du soleil. Toutes les orbites sont respectées selon le modèle suivant2.
// Inclinaison des orbits
list_orbit[0].position.y = 7.005 * Math.PI/180; // Mercure
list_orbit[1].position.y = 3.39 * Math.PI/180; // Venus
list_orbit[3].position.y = 1.8506 * Math.PI/180; // Mars
list_orbit[4].position.y = 1.304 * Math.PI/180; // Jupiter
list_orbit[5].position.y = 2.4845 * Math.PI/180; // Saturne
list_orbit[6].position.y = 0.7725 * Math.PI/180; // Uranus
list_orbit[7].position.y = 1.7692 * Math.PI/180; // Nepture
list_orbit[8].position.y = 17.1417 * Math.PI/180; // PlutonVoici un exemple de code qui permet d'ajouter les planètes à une orbite.
var list_orbit = []
for(planet in list_planet){
// list_planet contient toutes les planètes
var planet1 = list_planet[planet];
// On ajout un nouveau groupe à la list_orbit
list_orbit.push(new THREE.Group());
// On ajoute l'orbit au système solaire.
systemeSolaire.add(list_orbit[planet]);
// Par la suite, on ajoute la planète à l'orbit.
list_orbit[planet].add(planet1);
}Il est maintenant possible de contrôler chaque orbite. Pour réaliser la gravité autour du soleil. Il faut connaitre la distance entre la planète et le soleil. La vitesse à laquelle la planète orbite et l'angle de la planète.
Pour permettre de mieux visualiser les orbites, des lignes ont été ajoutées au modèle.
Ses lignes semblent simples à implémenté, mais la logique derrière ma produit quelque maux de tête.
Premièrement, est-ce que les lignes devaient être attaché à l'orbite ou être dessinées par rapport à la distance de la planète et le soleil ? J'ai choisi la deuxième option. J'ai ajouté les lignes par rapport au système solaire et la planète.
Pour ne pas trop consommer la mémoire, j'ai limité le nombre de vertice à chaque ligne. On peut voir que la dernière ligne de gravitation devient des lignes droites par moment. Maintenant, regardons le code.
var MAX_TRAIL_VERTICES = 500;
function createLineOrbit(x,y,z){
var trailGeometry = new THREE.Geometry();
for(var i = 0; i< MAX_TRAIL_VERTICES;i++){
trailGeometry.vertices.push(new THREE.Vector3(x,y,z));
}
var trailMaterial = new THREE.LineBasicMaterial({linewidth: 100});
var line = new THREE.Line(trailGeometry,trailMaterial);
return line;
}Lorsque la fonction createLineOrbit est appelée, elle créer une nouvelle instance de ligne contenant 500 vertices au maximum.
Dans le rendu, on appelle la fonction qui dessine les lignes.
if (Math.floor((Math.random()*10)%2)==0)
leaveTrail(orbi);On ne doit pas générer la ligne à tous les frames. Il faut créer une fonction qui écrème l'appel à cette fonction.
// utils.js
function leaveTrail(orbit) {
orbit.line.geometry.vertices.unshift(new THREE.Vector3().copy(orbit.position));
orbit.line.geometry.vertices.length = MAX_TRAIL_VERTICES;
orbit.line.geometry.verticesNeedUpdate = true;
};Lorsque cette fonction est appelée, on ajoute un nouveau vecteur au début de la liste3 et coupe la longueur de la liste des vertices avec notre MAX_TRAIL_VERTICES. On s'assure que les vertices peuvent être mis à jour par la suite.
L'orbit des planètes va être contrôlée dans la fonction render de three.js. À chaque frames, il faut repositionner les planètes. Ce mouvement pourrait être traduit par une translation.
for (planet in list_planet){
// On itère sur chaque planet
var pla = list_planet[planet]
// On ajuste l'angle de la planète selon la vitesse.
pla.angle += pla.speed;
// Permet de tourner autour de la planète.
var radius = pla.angle * Math.PI/180;
var orbi = list_orbit[planet]
// On permet à la planète de tourner sur elle même.
pla.rotation.y += 0.01;
// Translation de l'orbit qui contient la planète.
orbi.position.x = Math.cos(radius) * pla.orbitRadius;
orbi.position.z = Math.sin(radius) * pla.orbitRadius;
}La lune est un cas particulier de rotation.Elle n'a pas le même fonctionnement que les gravitations présentées ci-haut. Un groupe espacePlanet contient la planète terre et la Lune. Au lieu de déplacer la lune selon la distance avec la terre. La lune est positionnée à un endroit X à partie de la terre et on fait la rotation espacePlanet. Ce qui produit la rotation de la lune.
espacePlanet.rotation.y += 0.020;Voici un exemple de rotation de la terre et de la lune.
Il est possible d'ajouter d'autre planète à l'espace. Il y a un script generateurPlanet qui permet d'ajouter des planètes.le script créer aussi les vertexShader et les fragmentShader. Il suffit d'ajouter un nom de planète à la liste de planète.
La gravitation autour du soleil a été une tâche assez complexe. Il fallait avoir quelques bases de vecteur et de rotation autour d’un axe. Le phong shader a été aussi une tâche complexe. La texture devait être ajoutée à la formule mathématique de la projection de la lumière à notre fragmentShader.
Le modèle du système solaire pourrait être amélioré. La distance, la vitesse et les angles des planètes pourraient être ajoutés pour donner plus de réalistes au modèle. Il aurait été aussi intéressant d'ajouter du relief et le mode nuit aux planètes pour obtenir plus d'immersion.
L'intégration dans un environnement VR aurait été très amusante.