In-memory immutable R-tree implementation for n dimensions.
Status: in development
An R-tree is a commonly used spatial index.
This was fun to make, has an elegant concise algorithm, is thread-safe, fast, and reasonably memory efficient (uses structural sharing).
The algorithm to achieve immutability is cute. For insertion/deletion it involves recursion down to the required leaf node then recursion back up to replace the parent nodes up to the root. The guts of it is in Leaf.java and NonLeaf.java.
Iterator support requires a bookmark to be kept for a position in the tree and returned to later to continue traversal. An immutable stack containing the node and child index of the path nodes came to the rescue here and recursion was abandoned in favour of looping to prevent stack overflow (unfortunately java doesn't support tail recursion!).
Maven site reports are here including javadoc.
- supports n dimensions
- immutable R-tree suitable for concurrency
- Guttman's heuristics (Quadratic splitter) (paper)
- R*-tree heuristics (paper)
- Customizable splitter and selector
- search is
O(log(n))on average - insert, delete are
O(n)worst case - balanced delete
- uses structural sharing
- JMH benchmarks
- visualizer included
- decent unit test code coverage
- R*-tree performs ? searches/second returning 22 entries from a tree of 38,377 Greek earthquake locations on i7-920@2.67Ghz (maxChildren=4, minChildren=1). Insert at ? entries per second.
- requires java 1.8 or later
Number of points = 1000, max children per node 8:
| Quadratic split | R*-tree split |
|---|---|
 |
 |
Notice that there is little overlap in the R*-tree split compared to the Quadratic split. This should provide better search performance (and in general benchmarks show this).
Given the 38,377 data points of greek earthquakes (lat, long, time) from 1964 to 2000, the data is scanned to establish the ranges for each coordinate then normalized to a [0,1] range. The points are shuffled then added to an R-tree with minChildren=2 and maxChildren=4 using either the R* heuristics or standard R-tree heuristics. Visualization of the bounding boxes at nodes by method and depth is below.
The plots below are generated from the same shuffle of data points.
| Quadratic split | R*-tree split |
|---|---|
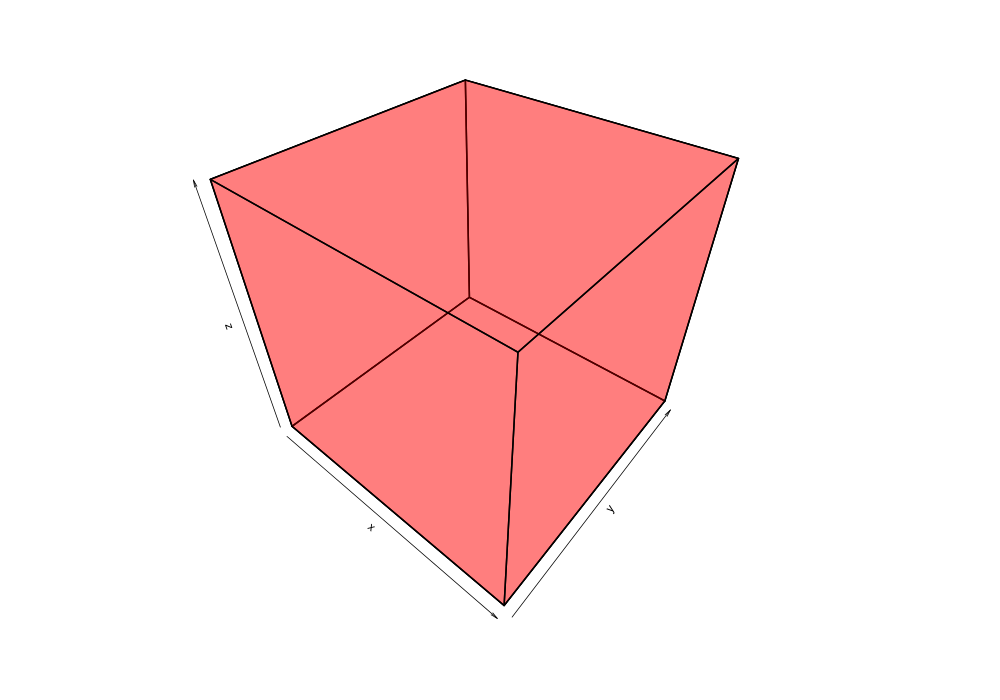 |
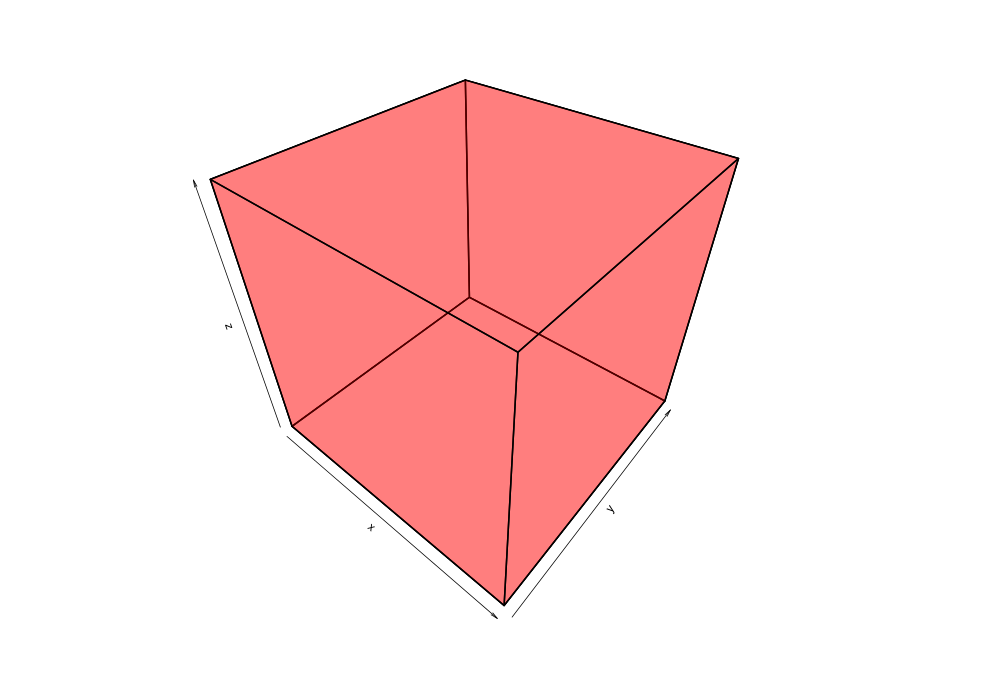 |
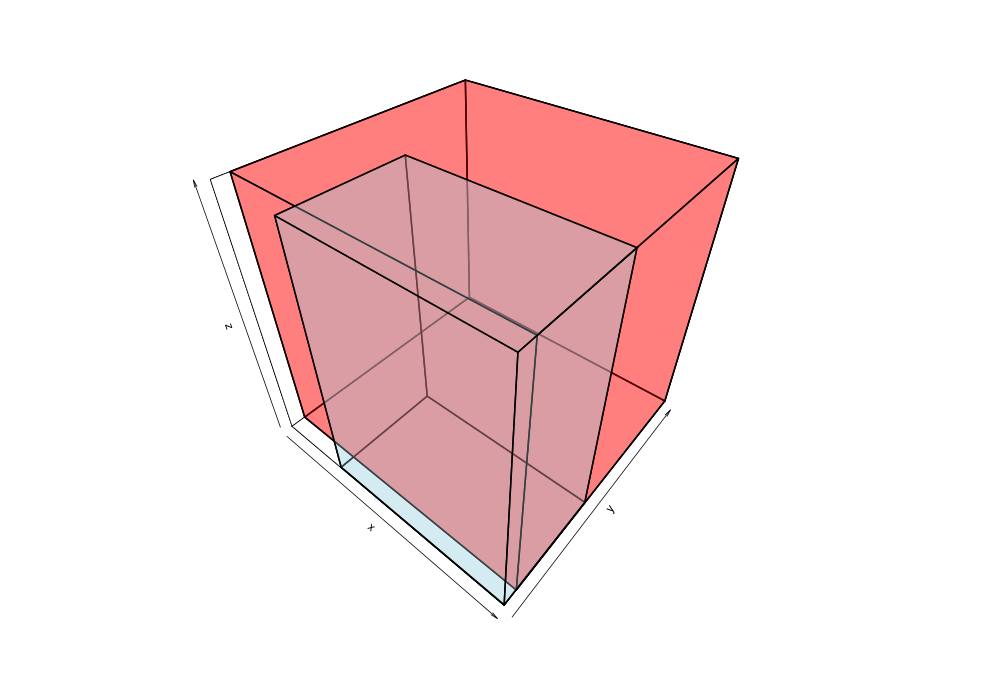 |
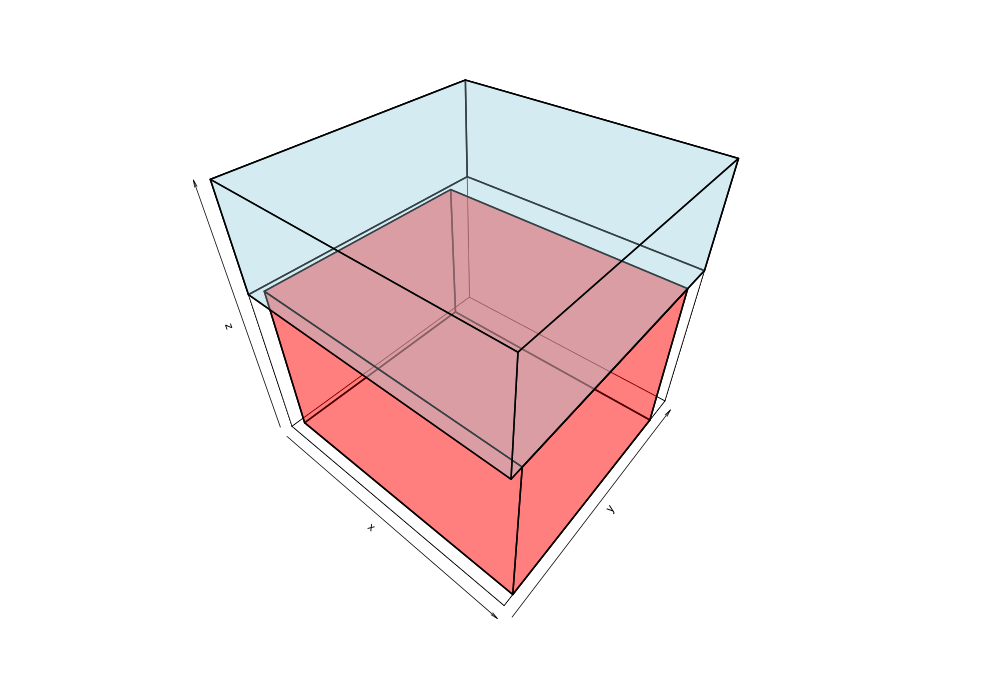 |
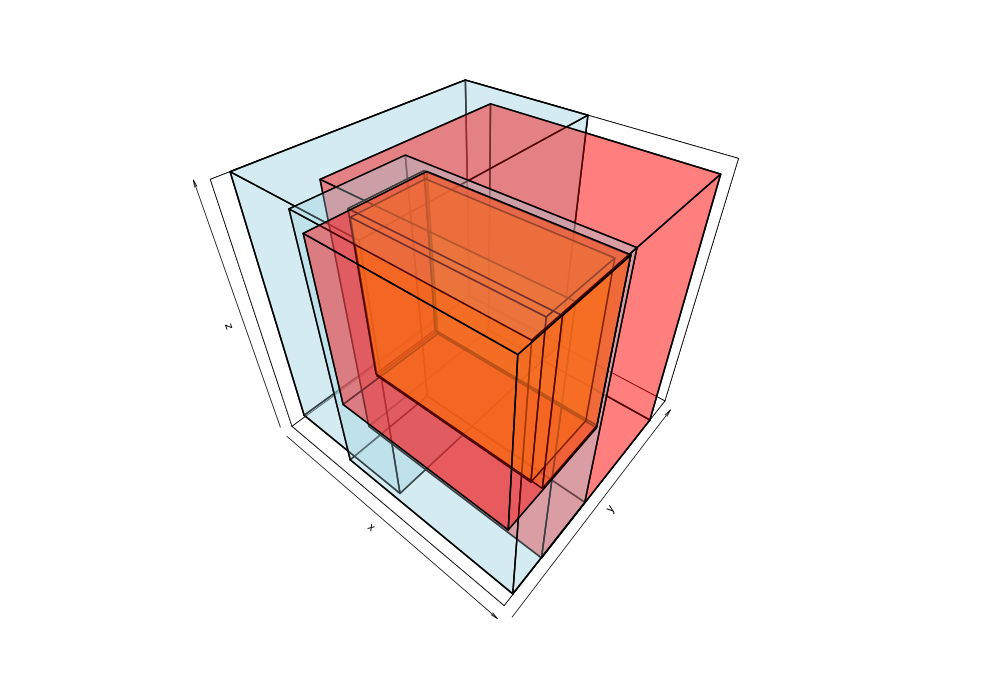 |
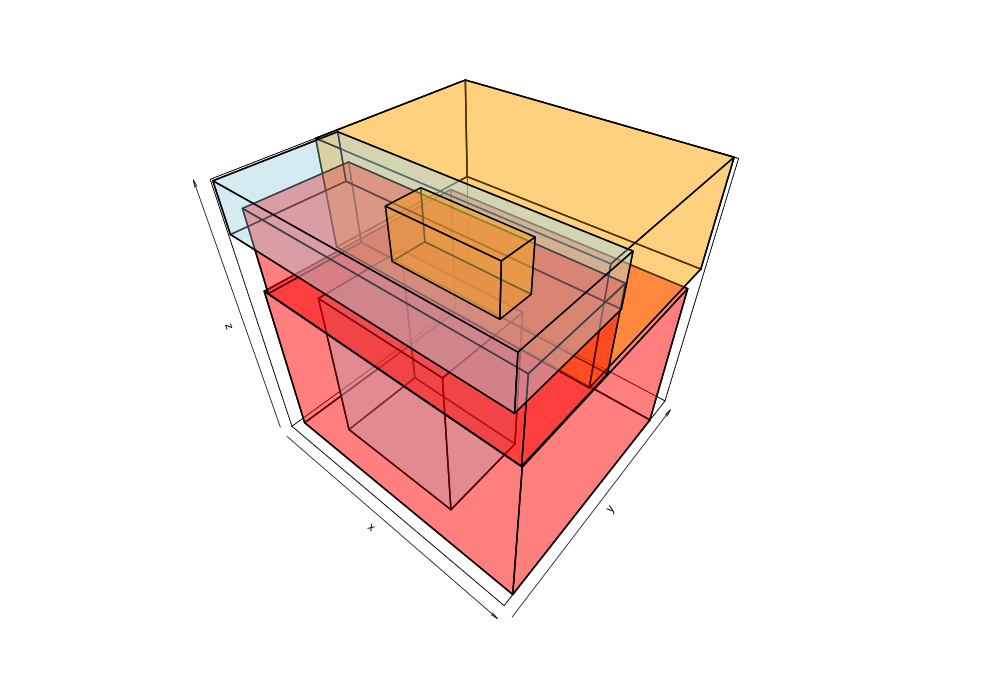 |
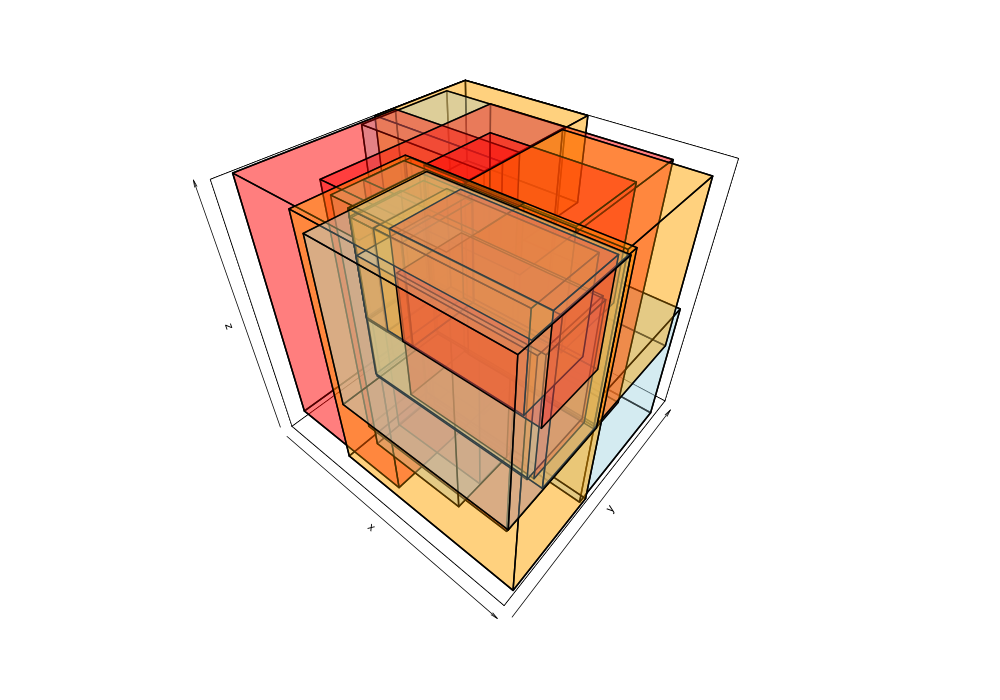 |
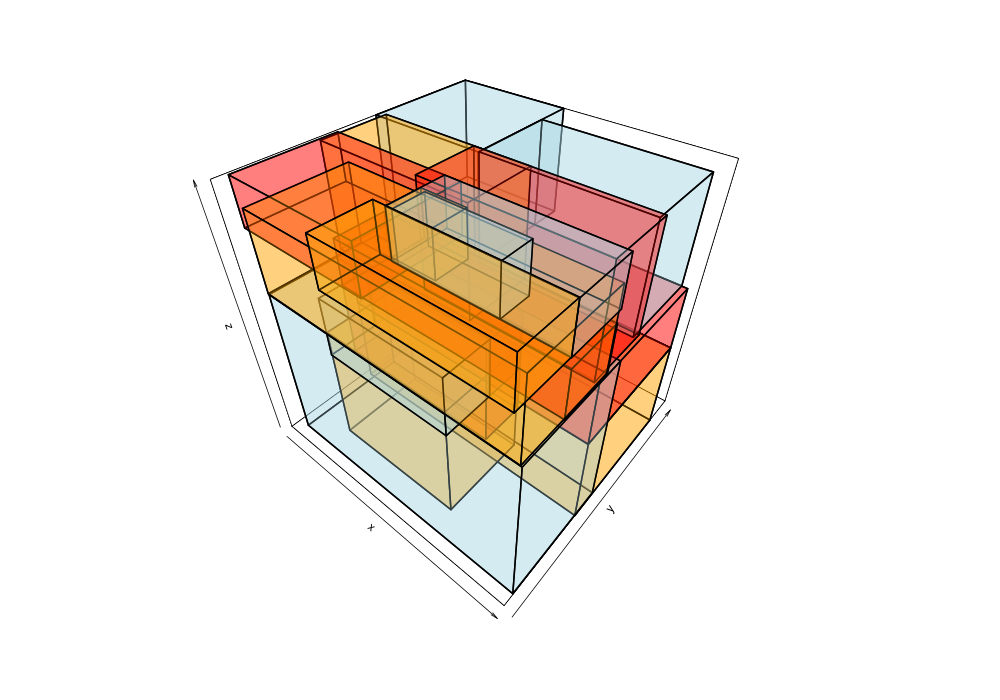 |
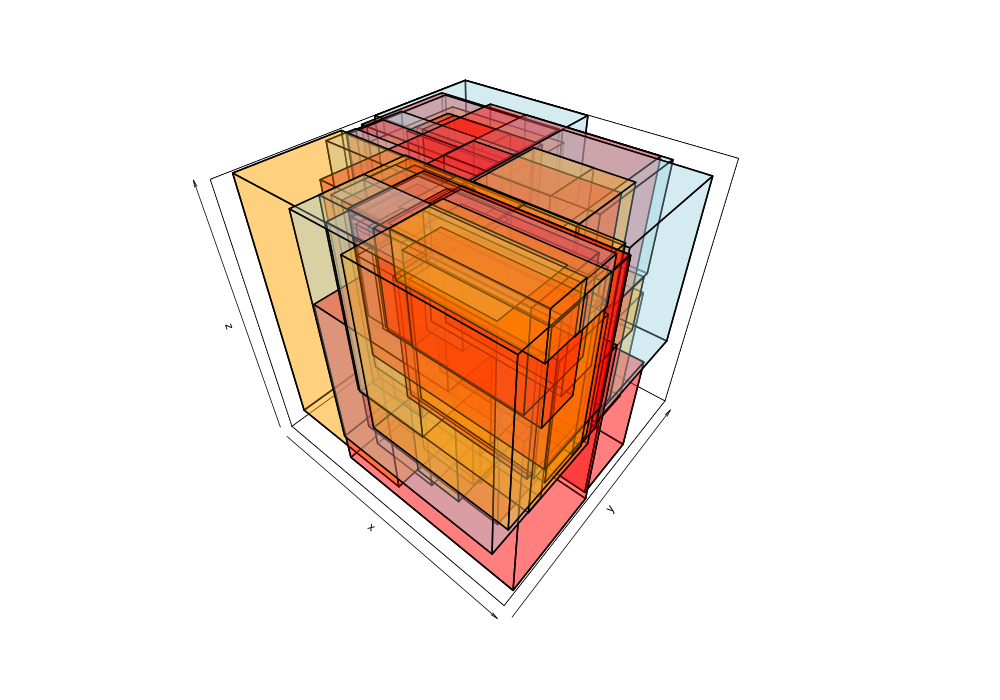 |
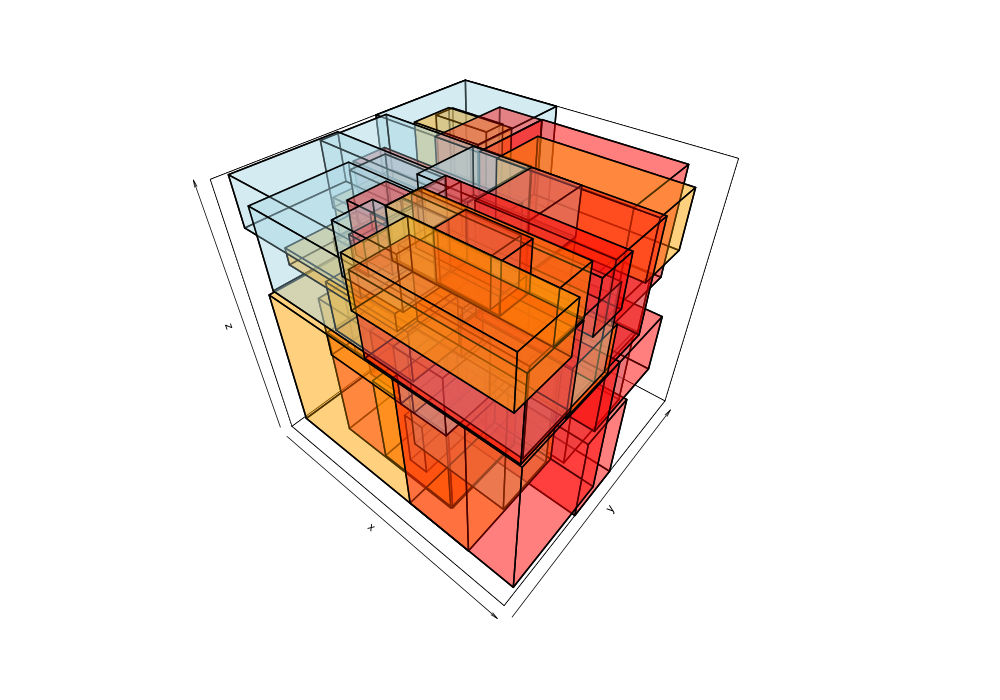 |
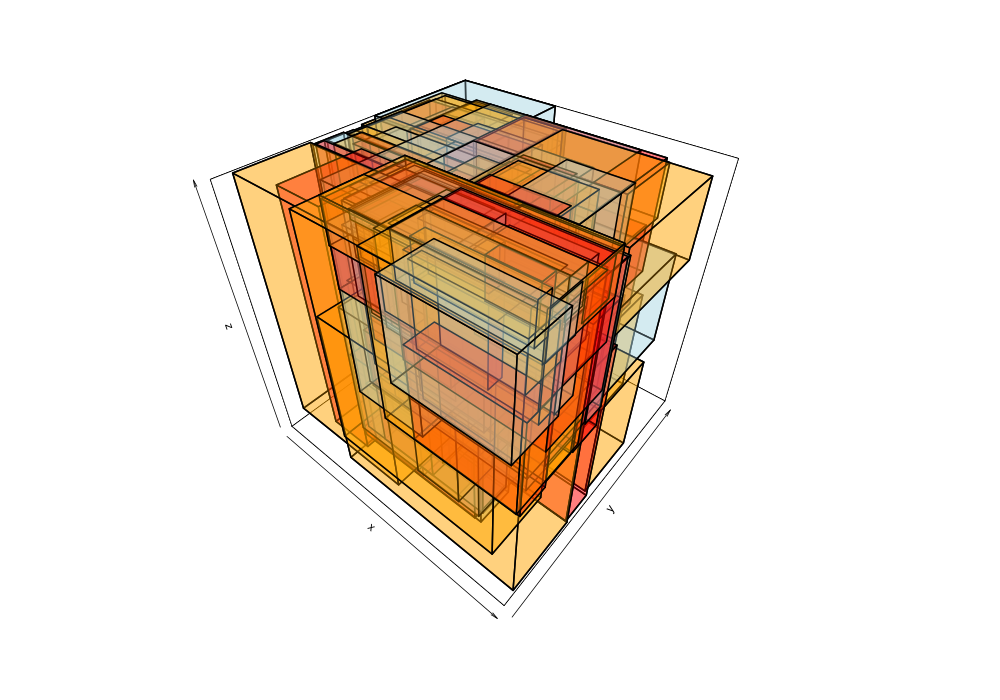 |
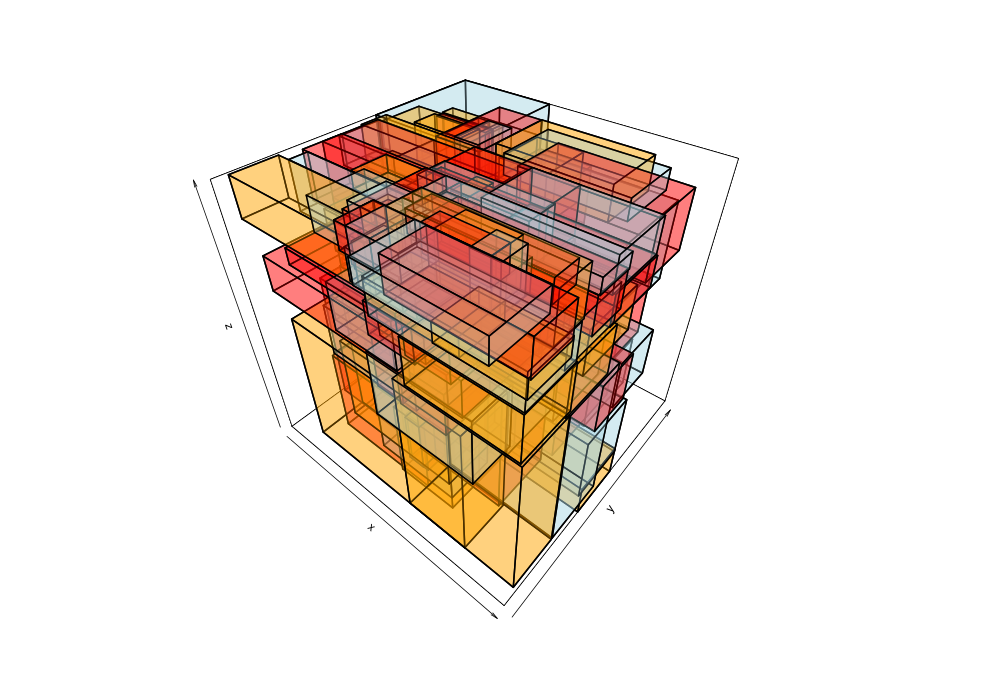 |
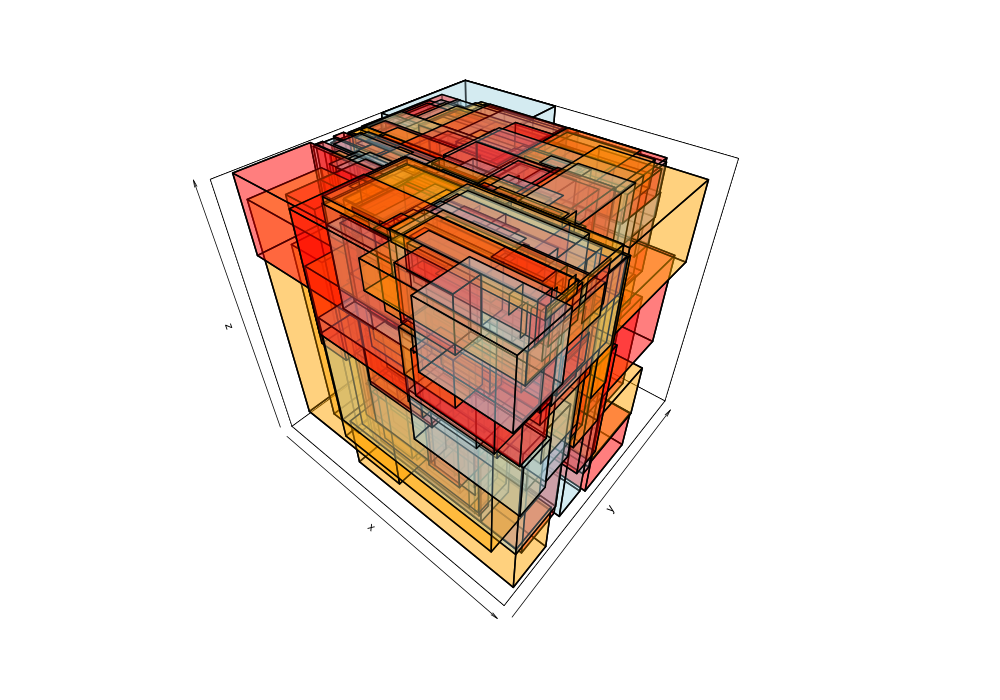 |
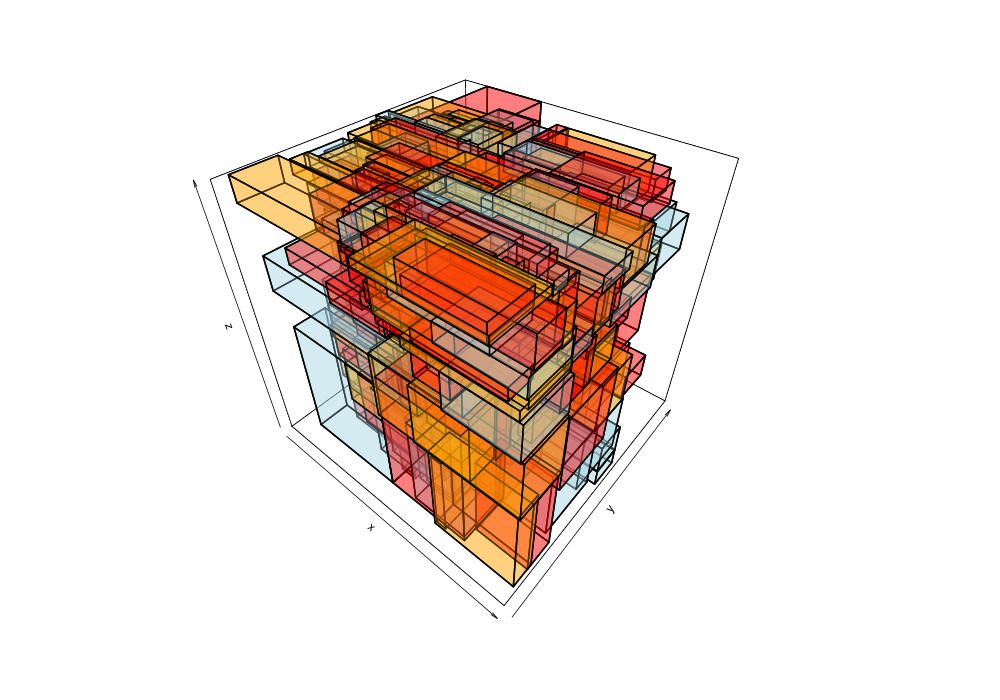 |
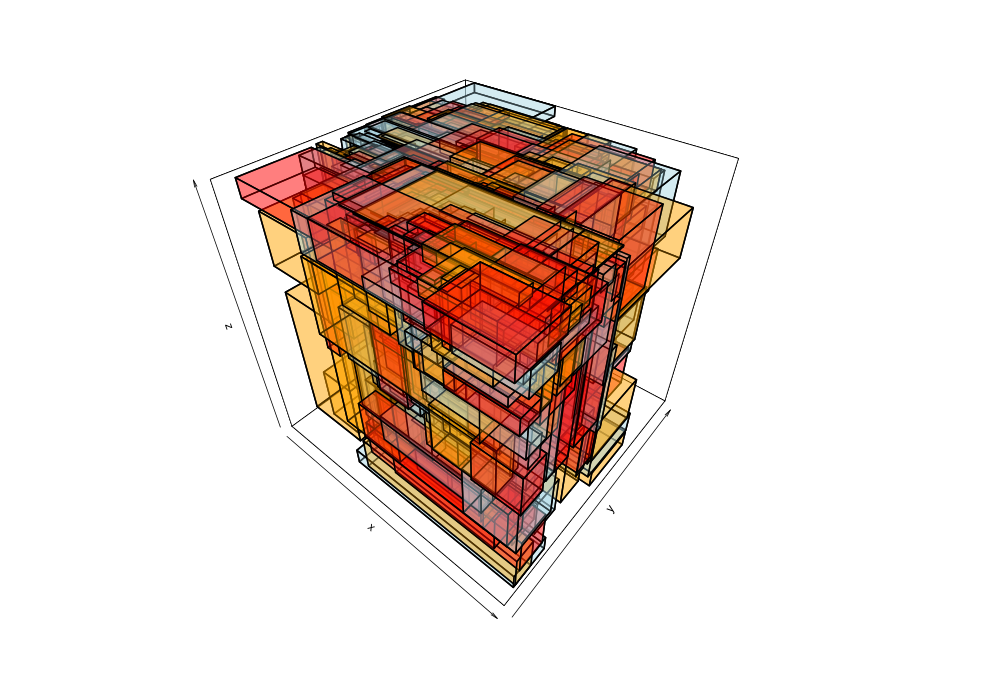 |
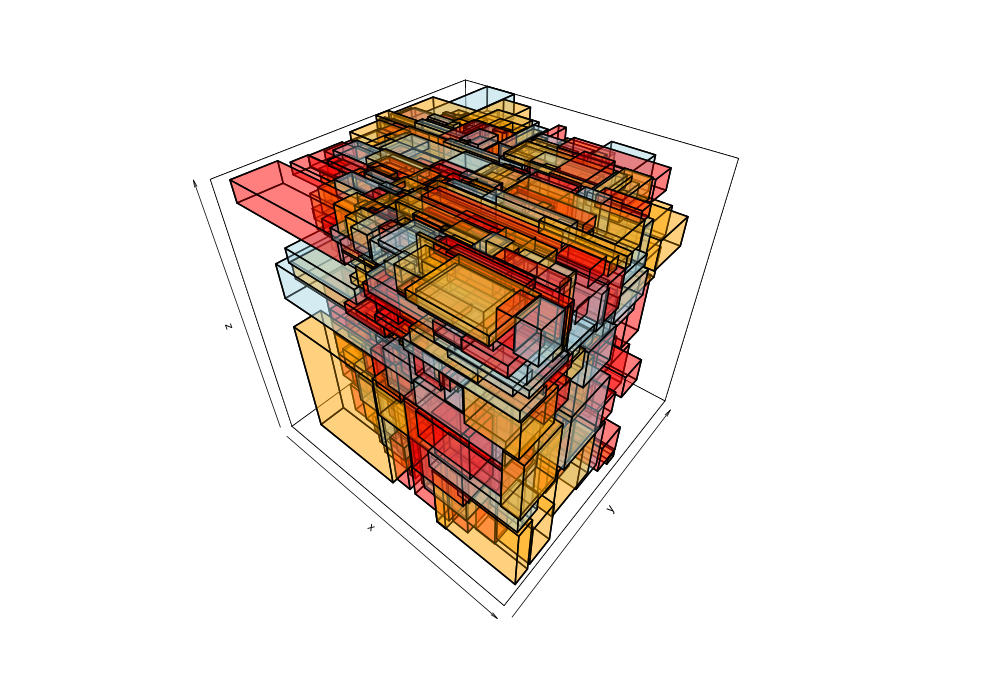 |
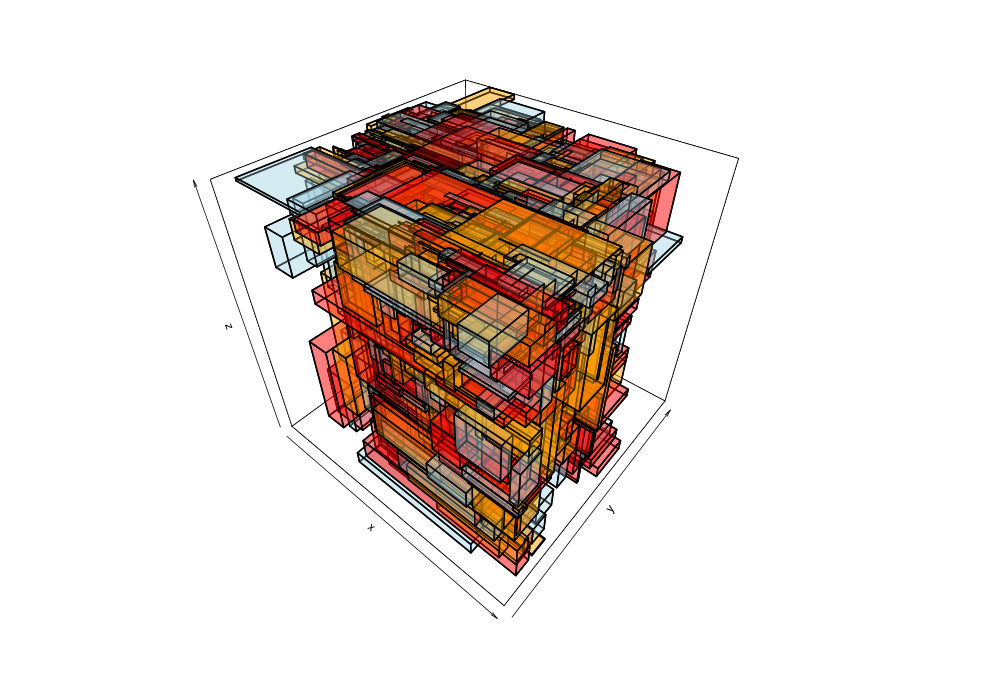 |
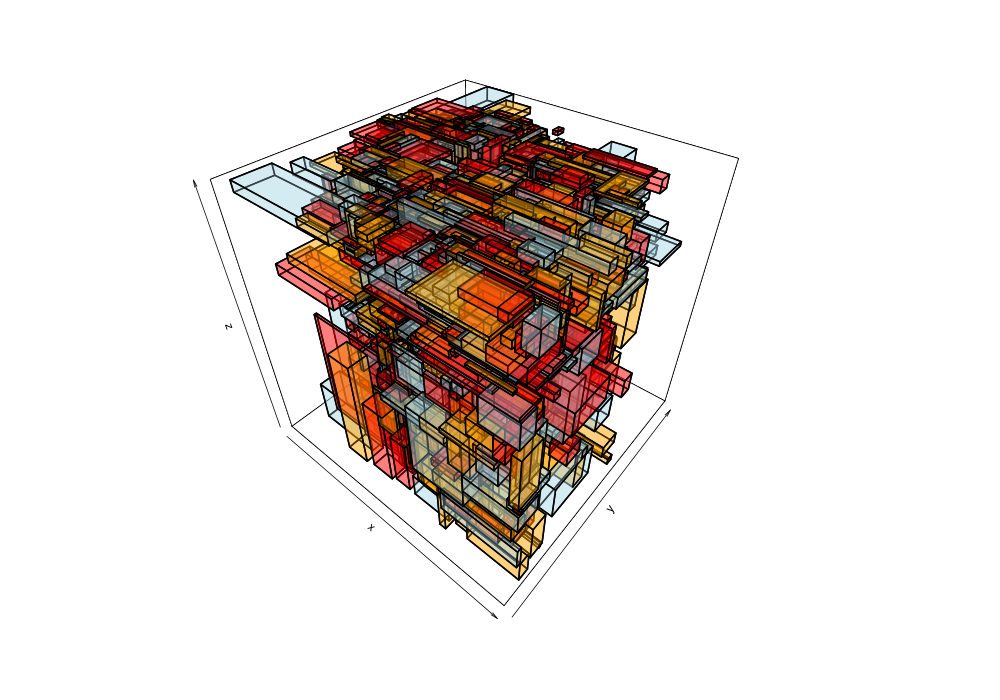 |
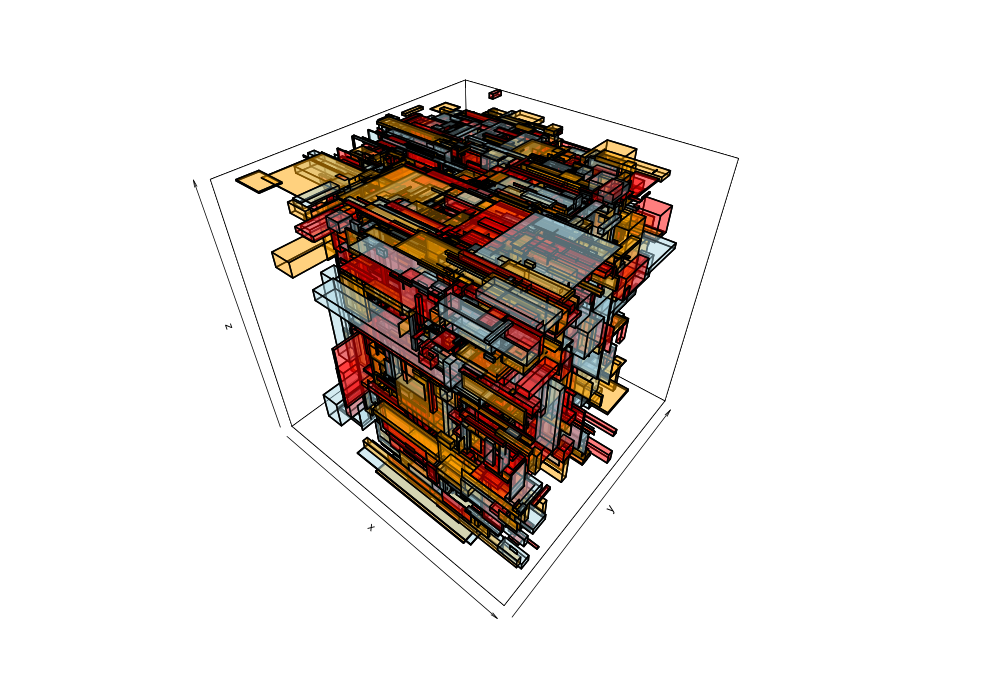 |
 |
Add this maven dependency to your pom.xml:
<dependency>
<groupId>com.github.davidmoten</groupId>
<artifactId>rtree-multi</artifactId>
<version>VERSION_HERE</version>
</dependency>Use the static builder methods on the RTree class:
// create an R-tree using Quadratic split with max
// children per node 4, min children 2 (the threshold
// at which members are redistributed)
RTree<String, Geometry> tree = RTree.create();You can specify a few parameters to the builder, including minChildren, maxChildren, splitter, selector:
RTree<String, Geometry> tree = RTree.minChildren(3).maxChildren(6).create();The following geometries are supported for insertion in an RTree:
RectanglePoint
If for instance you know that the entry geometry is always Point then create an RTree specifying that generic type to gain more type safety:
RTree<String, Point> tree = RTree.create();If you'd like an R*-tree (which uses a topological splitter on minimal margin, overlap area and area and a selector combination of minimal area increase, minimal overlap, and area):
RTree<String, Geometry> tree = RTree.star().maxChildren(6).create();
See benchmarks below for some of the performance differences.
When you add an item to the R-tree you need to provide a geometry that represents the 2D physical location or extension of the item. You can use these factory methods to create your geometries:
Rectangle.createPoint.create
To add an item to an R-tree:
RTree<T,Geometry> tree = RTree.dimensions(3).create();
tree = tree.add(item, Point.create(10, 20, 30));or
tree = tree.add(Entry.entry(item, Point.create(10, 20, 30));Important note: being an immutable data structure, calling tree.add(item, geometry) does nothing to tree,
it returns a new RTree containing the addition. Make sure you use the result of the add!
To remove an item from an R-tree, you need to match the item and its geometry:
tree = tree.delete(item, Point.create(10, 20, 30));or
tree = tree.delete(entry);Important note: being an immutable data structure, calling tree.delete(item, geometry) does nothing to tree,
it returns a new RTree without the deleted item. Make sure you use the result of the delete!
You can also write your own implementation of Geometry. An implementation of Geometry needs to specify methods to:
- check intersection with a rectangle (you can reuse the distance method here if you want but it might affect performance)
- provide a minimum bounding rectangle
- implement
equalsandhashCodefor consistent equality checking - measure distance to a rectangle (0 means they intersect). Note that this method is only used for search within a distance so implementing this method is optional. If you don't want to implement this method just throw a
RuntimeException.
For the R-tree to be well-behaved, the distance function if implemented needs to satisfy these properties:
distance(r) >= 0 for all rectangles rif rectangle r1 contains r2 then distance(r1)<=distance(r2)distance(r) = 0 if and only if the geometry intersects the rectangle r
The advantage of an R-tree is the ability to search for items in a region reasonably quickly.
On average search is O(log(n)) but worst case is O(n).
Search methods return Iterable sequences:
Iterable<Entry<T, Geometry>> results =
tree.search(Rectangle.create(0, 0, 2, 2));or search for items within a distance from the given geometry:
Iterable<Entry<T, Geometry>> results =
tree.search(Rectangle.create(0, 0, 2, 2), 5.0);To return all entries from an R-tree:
Iterable<Entry<T, Geometry>> results = tree.entries();Suppose you make a custom geometry like Polygon and you want to search an RTree<String, Point> for points inside the polygon. This is how you do it:
RTree<String, Point> tree = RTree.dimensions(2).create();
Func2<Point, Polygon, Boolean> pointInPolygon = ...
Polygon polygon = ...
...
entries = tree.search(polygon, pointInPolygon);The key is that you need to supply the intersects function (pointInPolygon) to the search. It is on you to implement that for all types of geometry present in the RTree. This is one reason that the generic Geometry type was added in rtree 0.5 (so the type system could tell you what geometry types you needed to calculate intersection for) .
As per the example above to do a proximity search you need to specify how to calculate distance between the geometry you are searching and the entry geometries:
RTree<String, Point> tree = RTree.create();
Func2<Point, Polygon, Boolean> distancePointToPolygon = ...
Polygon polygon = ...
...
entries = tree.search(polygon, 10, distancePointToPolygon);import com.github.davidmoten.rtree-multi.RTree;
RTree<String, Point> tree = RTree.maxChildren(5).create();
tree = tree.add("DAVE", Point.create(10, 20))
.add("FRED", Point.create(12, 25))
.add("MARY", Point.create(97, 125));
Iterable<Entry<String, Point>> entries =
tree.search(Rectangle.create(8, 15, 30, 35));Check out the benchmarks below, but I recommend you do your own benchmarks because every data set will behave differently. If you don't want to benchmark then use the defaults. General rules based on the benchmarks:
- for data sets of <10,000 entries use the default R-tree (quadratic splitter with maxChildren=4)
- for data sets of >=10,000 entries use the star R-tree (R*-tree heuristics with maxChildren=4 by default)
Watch out though, the benchmark data sets had quite specific characteristics. The 1000 entry dataset was randomly generated (so is more or less uniformly distributed) and the Greek dataset was earthquake data with its own clustering characteristics.
To minimize memory use you can use geometries that store single precision decimal values (float) instead of double precision (double). Here are examples:
// create geometry using double precision
Rectangle r = Rectangle.create(1.0, 2.0, 3.0, 4.0);
// create geometry using single precision
Rectangle r = Rectangle.create(1.0f, 2.0f, 3.0f, 4.0f);To visualize a 2D R-tree (only) in a PNG file of size 600 by 600 pixels just call:
tree.visualize(600,600)
.save("target/mytree.png");The result is like the images in the Features section above.
The RTree.asString() method returns output like this:
mbr=Rectangle [mins=[10.0, 4.0], maxes=[62.0, 85.0]]
mbr=Rectangle [mins=[28.0, 4.0], maxes=[34.0, 85.0]]
entry=Entry [value=2, geometry=Point [29.0, 4.0]]
entry=Entry [value=1, geometry=Point [28.0, 19.0]]
entry=Entry [value=4, geometry=Point [34.0, 85.0]]
mbr=Rectangle [mins=[10.0, 45.0], maxes=[62.0, 63.0]]
entry=Entry [value=5, geometry=Point [62.0, 45.0]]
entry=Entry [value=3, geometry=Point [10.0, 63.0]]
Serialization is not supported directly in rtree-multi. Your best bet is to serialize entries from and RTree as you like (just the entries) and then use bulk loading when deserializing. Bulk loading is performed like this:
// deserialize the entries from disk (for example)
List<Entry<Thing, Point> entries = ...
// bulk load
RTree<Thing, Point> tree = RTree.maxChildren(28).star().create(entries); git clone https://github.com/davidmoten/rtree-multi.git
cd rtree-multi
mvn clean install
Benchmarks are provided by
mvn clean install -P benchmark
The Greek data referred to in the benchmarks is a collection of some 38,377 entries corresponding to the epicentres of earthquakes in Greece between 1964 and 2000. This data set is used by multiple studies on R-trees as a test case.
These were run on i7-920 @2.67GHz with rtree version 0.9-RC1:
# JMH version: 1.21
# VM version: JDK 1.8.0_201, Java HotSpot(TM) 64-Bit Server VM, 25.201-b09
# VM invoker: /usr/lib/jvm/java-8-oracle/jre/bin/java
# VM options: -Xmx512m
# Warmup: 3 iterations, 10 s each
# Measurement: 10 iterations, 10 s each
# Timeout: 10 min per iteration
# Threads: 1 thread, will synchronize iterations
# Benchmark mode: Throughput, ops/time
Benchmark Mode Cnt Score Error Units
BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren004 thrpt 10 1021844.129 ± 16977.542 ops/s
BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren010 thrpt 10 931789.301 ± 33477.764 ops/s
BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren032 thrpt 10 304816.886 ± 5674.364 ops/s
BenchmarksRTree.rStarTreeSearchOf1000PointsMaxChildren128 thrpt 10 606188.199 ± 7553.533 ops/s
BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren004 thrpt 10 527595.512 ± 34400.389 ops/s
BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren010 thrpt 10 194793.663 ± 5385.855 ops/s
BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren032 thrpt 10 297597.166 ± 40175.027 ops/s
BenchmarksRTree.rStarTreeSearchOfGreekDataPointsMaxChildren128 thrpt 10 221605.832 ± 9332.555 ops/s
BenchmarksRTree.searchNearestGreek thrpt 10 3534.733 ± 177.370 ops/s