comments	edit_url
true	https://github.com/doocs/leetcode/edit/main/lcof2/%E5%89%91%E6%8C%87%20Offer%20II%20096.%20%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%BA%A4%E7%BB%87/README.md

剑指 Offer II 096. 字符串交织

题目描述

给定三个字符串 s1、s2、s3，请判断 s3 能不能由 s1 和 s2 交织（交错） 组成。

两个字符串 s 和 t 交织的定义与过程如下，其中每个字符串都会被分割成若干非空子字符串：

s = s₁ + s₂ + ... + s_n
t = t₁ + t₂ + ... + t_m
|n - m| <= 1
交织是 s₁ + t₁ + s₂ + t₂ + s₃ + t₃ + ... 或者 t₁ + s₁ + t₂ + s₂ + t₃ + s₃ + ...

提示：a + b 意味着字符串 a 和 b 连接。

示例 1：

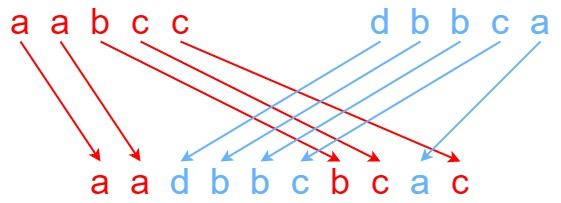
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成

注意：本题与主站 97 题相同： https://leetcode.cn/problems/interleaving-string/

解法

方法一：记忆化搜索

我们记字符串 $s_1$ 的长度为 $m$，字符串 $s_2$ 的长度为 $n$，如果 $m + n \neq |s_3|$，那么 $s_3$ 一定不是 $s_1$ 和 $s_2$ 的交错字符串，返回 false。

接下来，我们设计一个函数 $dfs(i, j)$，表示从 $s_1$ 的第 $i$ 个字符和 $s_2$ 的第 $j$ 个字符开始，能否交错组成 $s_3$ 的剩余部分。那么答案就是 $dfs(0, 0)$。

函数 $dfs(i, j)$ 的计算过程如下：

如果 $i \geq m$ 并且 $j \geq n$，那么说明 $s_1$ 和 $s_2$ 都已经遍历完毕，返回 true。

如果 $i < m$ 并且 $s_1[i] = s_3[i + j]$，那么说明 $s_1[i]$ 这个字符是 $s_3[i + j]$ 中的一部分，因此递归地调用 $dfs(i + 1, j)$ 判断 $s_1$ 的下一个字符能否和 $s_2$ 的当前字符匹配，如果能匹配成功，就返回 true。

同理，如果 $j < n$ 并且 $s_2[j] = s_3[i + j]$，那么说明 $s_2[j]$ 这个字符是 $s_3[i + j]$ 中的一部分，因此递归地调用 $dfs(i, j + 1)$ 判断 $s_2$ 的下一个字符能否和 $s_1$ 的当前字符匹配，如果能匹配成功，就返回 true。

否则，返回 false。

为了避免重复计算，我们可以使用记忆化搜索。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是字符串 $s_1$ 和 $s_2$ 的长度。

Python3

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        @cache
        def dfs(i: int, j: int) -> bool:
            if i >= m and j >= n:
                return True
            k = i + j
            if i < m and s1[i] == s3[k] and dfs(i + 1, j):
                return True
            if j < n and s2[j] == s3[k] and dfs(i, j + 1):
                return True
            return False

        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        return dfs(0, 0)

Java

class Solution {
    private Map<List<Integer>, Boolean> f = new HashMap<>();
    private String s1;
    private String s2;
    private String s3;
    private int m;
    private int n;

    public boolean isInterleave(String s1, String s2, String s3) {
        m = s1.length();
        n = s2.length();
        if (m + n != s3.length()) {
            return false;
        }
        this.s1 = s1;
        this.s2 = s2;
        this.s3 = s3;
        return dfs(0, 0);
    }

    private boolean dfs(int i, int j) {
        if (i >= m && j >= n) {
            return true;
        }
        var key = List.of(i, j);
        if (f.containsKey(key)) {
            return f.get(key);
        }
        int k = i + j;
        boolean ans = false;
        if (i < m && s1.charAt(i) == s3.charAt(k) && dfs(i + 1, j)) {
            ans = true;
        }
        if (!ans && j < n && s2.charAt(j) == s3.charAt(k) && dfs(i, j + 1)) {
            ans = true;
        }
        f.put(key, ans);
        return ans;
    }
}

C++

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) {
            return false;
        }
        vector<vector<int>> f(m + 1, vector<int>(n + 1, -1));
        function<bool(int, int)> dfs = [&](int i, int j) {
            if (i >= m && j >= n) {
                return true;
            }
            if (f[i][j] != -1) {
                return f[i][j] == 1;
            }
            f[i][j] = 0;
            int k = i + j;
            if (i < m && s1[i] == s3[k] && dfs(i + 1, j)) {
                f[i][j] = 1;
            }
            if (!f[i][j] && j < n && s2[j] == s3[k] && dfs(i, j + 1)) {
                f[i][j] = 1;
            }
            return f[i][j] == 1;
        };
        return dfs(0, 0);
    }
};

Go

func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}

	f := map[int]bool{}
	var dfs func(int, int) bool
	dfs = func(i, j int) bool {
		if i >= m && j >= n {
			return true
		}
		if v, ok := f[i*200+j]; ok {
			return v
		}
		k := i + j
		f[i*200+j] = (i < m && s1[i] == s3[k] && dfs(i+1, j)) || (j < n && s2[j] == s3[k] && dfs(i, j+1))
		return f[i*200+j]
	}
	return dfs(0, 0)
}

TypeScript

function isInterleave(s1: string, s2: string, s3: string): boolean {
    const m = s1.length;
    const n = s2.length;
    if (m + n !== s3.length) {
        return false;
    }
    const f: number[][] = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    const dfs = (i: number, j: number): boolean => {
        if (i >= m && j >= n) {
            return true;
        }
        if (f[i][j]) {
            return f[i][j] === 1;
        }
        f[i][j] = -1;
        if (i < m && s1[i] === s3[i + j] && dfs(i + 1, j)) {
            f[i][j] = 1;
        }
        if (f[i][j] === -1 && j < n && s2[j] === s3[i + j] && dfs(i, j + 1)) {
            f[i][j] = 1;
        }
        return f[i][j] === 1;
    };
    return dfs(0, 0);
}

C#

public class Solution {
    private int m;
    private int n;
    private string s1;
    private string s2;
    private string s3;
    private int[,] f;

    public bool IsInterleave(string s1, string s2, string s3) {
        m = s1.Length;
        n = s2.Length;
        if (m + n != s3.Length) {
            return false;
        }
        this.s1 = s1;
        this.s2 = s2;
        this.s3 = s3;
        f = new int[m + 1, n + 1];
        return dfs(0, 0);
    }

    private bool dfs(int i, int j) {
        if (i >= m && j >= n) {
            return true;
        }
        if (f[i, j] != 0) {
            return f[i, j] == 1;
        }
        f[i, j] = -1;
        if (i < m && s1[i] == s3[i + j] && dfs(i + 1, j)) {
            f[i, j] = 1;
        }
        if (f[i, j] == -1 && j < n && s2[j] == s3[i + j] && dfs(i, j + 1)) {
            f[i, j] = 1;
        }
        return f[i, j] == 1;
    }
}

Swift

class Solution {
    private var memo = [String: Bool]()
    private var s1: [Character] = []
    private var s2: [Character] = []
    private var s3: [Character] = []
    private var m = 0
    private var n = 0

    func isInterleave(_ s1: String, _ s2: String, _ s3: String) -> Bool {
        m = s1.count
        n = s2.count
        if m + n != s3.count {
            return false
        }
        self.s1 = Array(s1)
        self.s2 = Array(s2)
        self.s3 = Array(s3)
        return dfs(0, 0)
    }

    private func dfs(_ i: Int, _ j: Int) -> Bool {
        if i >= m && j >= n {
            return true
        }
        let key = "\(i),\(j)"
        if let cached = memo[key] {
            return cached
        }
        let k = i + j
        var ans = false
        if i < m && s1[i] == s3[k] && dfs(i + 1, j) {
            ans = true
        }
        if !ans && j < n && s2[j] == s3[k] && dfs(i, j + 1) {
            ans = true
        }
        memo[key] = ans
        return ans
    }
}

方法二：动态规划

我们可以将方法一中的记忆化搜索转化为动态规划。

定义 $f[i][j]$ 表示字符串 $s_1$ 的前 $i$ 个字符和字符串 $s_2$ 的前 $j$ 个字符是否能交错组成字符串 $s_3$ 的前 $i + j$ 个字符。在进行状态转移时，我们可以考虑当前字符是由 $s_1$ 的最后一个字符还是 $s_2$ 的最后一个字符得到的，因此有状态转移方程：

$$ f[i][j] = \begin{cases} f[i - 1][j] & \textit{if } s_1[i - 1] = s_3[i + j - 1] \\ \textit{or } f[i][j - 1] & \textit{if } s_2[j - 1] = s_3[i + j - 1] \\ \textit{false} & \textit{otherwise} \end{cases} $$

其中 $f[0][0] = \textit{true}$ 表示空串是两个空串的交错字符串。

答案即为 $f[m][n]$。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是字符串 $s_1$ 和 $s_2$ 的长度。

我们注意到，状态 $f[i][j]$ 只和状态 $f[i - 1][j]$、$f[i][j - 1]$、$f[i - 1][j - 1]$ 有关，因此我们可以使用滚动数组优化空间复杂度，将空间复杂度优化到 $O(n)$。

Python3

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        f = [[False] * (n + 1) for _ in range(m + 1)]
        f[0][0] = True
        for i in range(m + 1):
            for j in range(n + 1):
                k = i + j - 1
                if i and s1[i - 1] == s3[k]:
                    f[i][j] = f[i - 1][j]
                if j and s2[j - 1] == s3[k]:
                    f[i][j] |= f[i][j - 1]
        return f[m][n]

Java

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int m = s1.length(), n = s2.length();
        if (m + n != s3.length()) {
            return false;
        }
        boolean[][] f = new boolean[m + 1][n + 1];
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0 && s1.charAt(i - 1) == s3.charAt(k)) {
                    f[i][j] = f[i - 1][j];
                }
                if (j > 0 && s2.charAt(j - 1) == s3.charAt(k)) {
                    f[i][j] |= f[i][j - 1];
                }
            }
        }
        return f[m][n];
    }
}

C++

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) {
            return false;
        }
        bool f[m + 1][n + 1];
        memset(f, false, sizeof(f));
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0 && s1[i - 1] == s3[k]) {
                    f[i][j] = f[i - 1][j];
                }
                if (j > 0 && s2[j - 1] == s3[k]) {
                    f[i][j] |= f[i][j - 1];
                }
            }
        }
        return f[m][n];
    }
};

Go

func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}
	f := make([][]bool, m+1)
	for i := range f {
		f[i] = make([]bool, n+1)
	}
	f[0][0] = true
	for i := 0; i <= m; i++ {
		for j := 0; j <= n; j++ {
			k := i + j - 1
			if i > 0 && s1[i-1] == s3[k] {
				f[i][j] = f[i-1][j]
			}
			if j > 0 && s2[j-1] == s3[k] {
				f[i][j] = (f[i][j] || f[i][j-1])
			}
		}
	}
	return f[m][n]
}

TypeScript

function isInterleave(s1: string, s2: string, s3: string): boolean {
    const m = s1.length;
    const n = s2.length;
    if (m + n !== s3.length) {
        return false;
    }
    const f: boolean[][] = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(false));
    f[0][0] = true;
    for (let i = 0; i <= m; ++i) {
        for (let j = 0; j <= n; ++j) {
            const k = i + j - 1;
            if (i > 0 && s1[i - 1] === s3[k]) {
                f[i][j] = f[i - 1][j];
            }
            if (j > 0 && s2[j - 1] === s3[k]) {
                f[i][j] = f[i][j] || f[i][j - 1];
            }
        }
    }
    return f[m][n];
}

C#

public class Solution {
    public bool IsInterleave(string s1, string s2, string s3) {
        int m = s1.Length, n = s2.Length;
        if (m + n != s3.Length) {
            return false;
        }
        bool[,] f = new bool[m + 1, n + 1];
        f[0, 0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0 && s1[i - 1] == s3[k]) {
                    f[i, j] = f[i - 1, j];
                }
                if (j > 0 && s2[j - 1] == s3[k]) {
                    f[i, j] |= f[i, j - 1];
                }
            }
        }
        return f[m, n];
    }
}

方法三

Python3

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        f = [True] + [False] * n
        for i in range(m + 1):
            for j in range(n + 1):
                k = i + j - 1
                if i:
                    f[j] &= s1[i - 1] == s3[k]
                if j:
                    f[j] |= f[j - 1] and s2[j - 1] == s3[k]
        return f[n]

Java

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int m = s1.length(), n = s2.length();
        if (m + n != s3.length()) {
            return false;
        }
        boolean[] f = new boolean[n + 1];
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0) {
                    f[j] &= s1.charAt(i - 1) == s3.charAt(k);
                }
                if (j > 0) {
                    f[j] |= (f[j - 1] & s2.charAt(j - 1) == s3.charAt(k));
                }
            }
        }
        return f[n];
    }
}

C++

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) {
            return false;
        }
        bool f[n + 1];
        memset(f, false, sizeof(f));
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i) {
                    f[j] &= s1[i - 1] == s3[k];
                }
                if (j) {
                    f[j] |= (s2[j - 1] == s3[k] && f[j - 1]);
                }
            }
        }
        return f[n];
    }
};

Go

func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}
	f := make([]bool, n+1)
	f[0] = true
	for i := 0; i <= m; i++ {
		for j := 0; j <= n; j++ {
			k := i + j - 1
			if i > 0 {
				f[j] = (f[j] && s1[i-1] == s3[k])
			}
			if j > 0 {
				f[j] = (f[j] || (s2[j-1] == s3[k] && f[j-1]))
			}
		}
	}
	return f[n]
}

TypeScript

function isInterleave(s1: string, s2: string, s3: string): boolean {
    const m = s1.length;
    const n = s2.length;
    if (m + n !== s3.length) {
        return false;
    }
    const f: boolean[] = new Array(n + 1).fill(false);
    f[0] = true;
    for (let i = 0; i <= m; ++i) {
        for (let j = 0; j <= n; ++j) {
            const k = i + j - 1;
            if (i) {
                f[j] = f[j] && s1[i - 1] === s3[k];
            }
            if (j) {
                f[j] = f[j] || (f[j - 1] && s2[j - 1] === s3[k]);
            }
        }
    }
    return f[n];
}

C#

public class Solution {
    public bool IsInterleave(string s1, string s2, string s3) {
        int m = s1.Length, n = s2.Length;
        if (m + n != s3.Length) {
            return false;
        }
        bool[] f = new bool[n + 1];
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0) {
                    f[j] &= s1[i - 1] == s3[k];
                }
                if (j > 0) {
                    f[j] |= (f[j - 1] & s2[j - 1] == s3[k]);
                }
            }
        }
        return f[n];
    }
}

Swift

class Solution {
    func isInterleave(_ s1: String, _ s2: String, _ s3: String) -> Bool {
        let m = s1.count, n = s2.count
        if m + n != s3.count {
            return false
        }

        let s1 = Array(s1), s2 = Array(s2), s3 = Array(s3)
        var dp = Array(repeating: Array(repeating: false, count: n + 1), count: m + 1)
        dp[0][0] = true

        for i in 0...m {
            for j in 0...n {
                let k = i + j - 1
                if i > 0 && s1[i - 1] == s3[k] {
                    dp[i][j] = dp[i][j] || dp[i - 1][j]
                }
                if j > 0 && s2[j - 1] == s3[k] {
                    dp[i][j] = dp[i][j] || dp[i][j - 1]
                }
            }
        }

        return dp[m][n]
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

剑指 Offer II 096. 字符串交织

题目描述

解法

方法一：记忆化搜索

Python3

Java

C++

Go

TypeScript

C#

Swift

方法二：动态规划

Python3

Java

C++

Go

TypeScript

C#

方法三

Python3

Java

C++

Go

TypeScript

C#

Swift

Files

README.md

Latest commit

History

README.md

File metadata and controls

剑指 Offer II 096. 字符串交织

题目描述

解法

方法一：记忆化搜索

Python3

Java

C++

Go

TypeScript

C#

Swift

方法二：动态规划

Python3

Java

C++

Go

TypeScript

C#

方法三

Python3

Java

C++

Go

TypeScript

C#

Swift