README.md

2360. Longest Cycle in a Graph

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

Example 1:

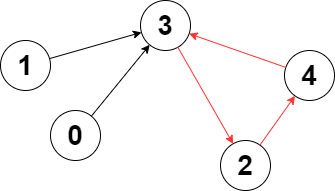
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

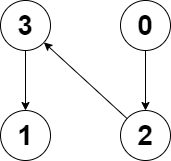
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

Solutions (Rust)

1. Solution

use std::collections::HashMap;

impl Solution {
    pub fn longest_cycle(edges: Vec<i32>) -> i32 {
        let mut visited = vec![false; edges.len()];
        let mut nodes = HashMap::new();
        let mut ret = -1;

        for i in 0..edges.len() {
            if visited[i] {
                continue;
            }

            let mut i = i;
            let mut count = 1;
            nodes.clear();

            while edges[i] != -1 {
                if let Some(&x) = nodes.get(&i) {
                    ret = ret.max(count - x);
                    break;
                } else if visited[i] {
                    break;
                }

                visited[i] = true;
                nodes.insert(i, count);
                i = edges[i] as usize;
                count += 1;
            }
        }

        ret
    }
}