README.rst

Finite-dimensional spaces of simple, fast, and highly-expressive diffeomorphisms derived from parametric, continuously-defined, velocity fields in Numpy and Pytorch. DIFW supports one-dimensional diffeomorphic transformations.

This repo is based on the libcpab library that supports diffeomorphic transformations in 1D (time series), 2D (images) and 3D (volumetric images). Thanks to Nicki Skafte Detlefsen, Oren Freifeld and Ron Shapira Weber for their help and guidance.

Getting Started

The following code transforms a regular grid using a diffeomorphic curve parametrized theta:

# Import difw library
import difw

# Transformation instance
T = difw.Cpab(tess_size=5, backend="numpy", device="cpu", zero_boundary=True, basis="qr")

# Generate grid
grid = T.uniform_meshgrid(100)

# Transformation parameters
theta = T.identity(epsilon=1)

# Transform grid
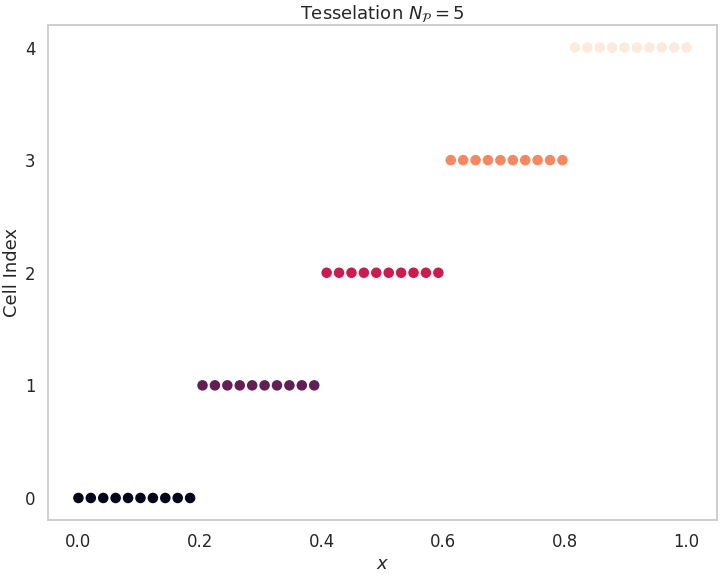
grid_t = T.transform_grid(grid, theta)

In this example, the tesselation is composed of 5 intervals, and the zero_boundary condition set to True constraints the velocity at the tesselation boundary (in this case, at x=0 and x=1). The regular grid has 100 equally spaced points.

T.visualize_tesselation()

The velocity field is formed by a continuous piecewise affine function defined over 5 intervals. The parameters theta represent a basis of the null space for all continuous piecewise affine functions composed of 5 intervals. In this case, we have used the QR decomposition to build the basis. See the API documentation for more details about the transformation options.

Taking into account the zero velocity constraints at the boundary, only 4 dimensions or degree of freedom are left to play with, and that indeed is the dimensionality of theta, a vector of 4 values.

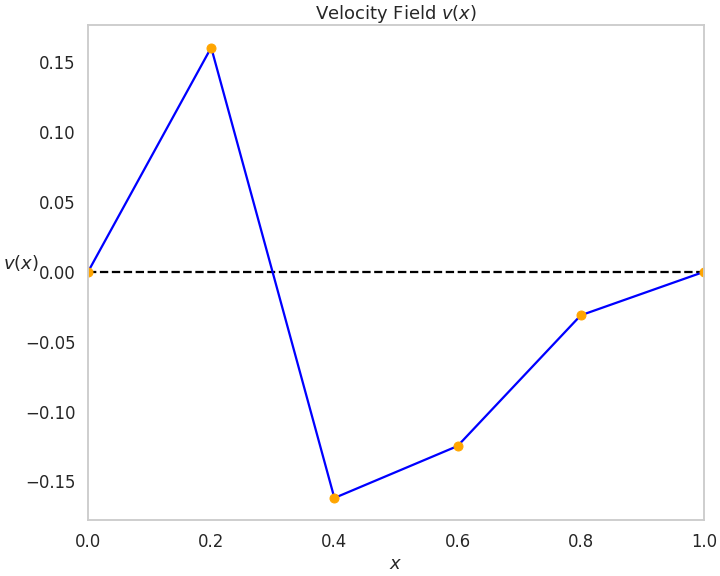
T.visualize_velocity(theta)

We can visualize the generated transformation based on the parameters theta:

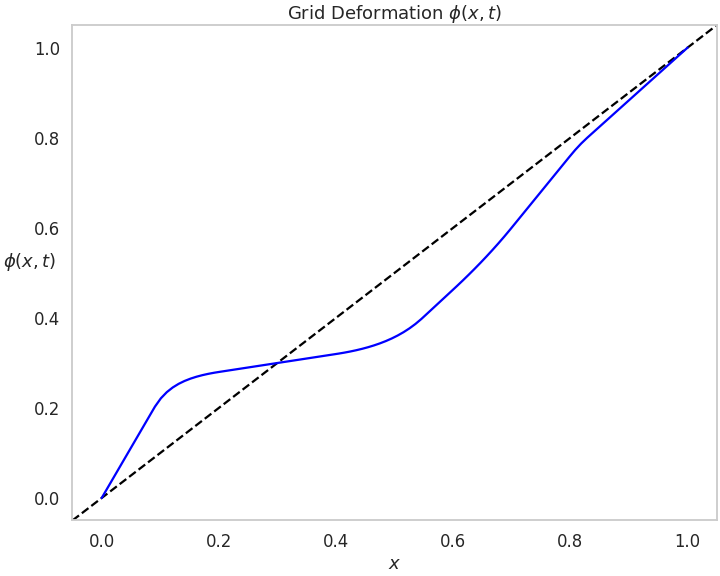
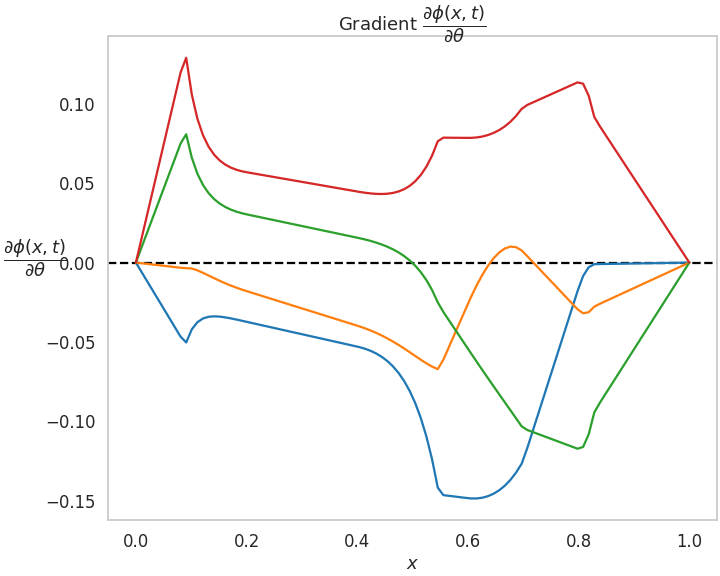
T.visualize_deformgrid(theta)

In addition, for optimization tasks, it is useful to obtain the gradient of the transformation with respect to parameters theta. The gradient function can be obtained in closed-form solution. There are 4 different functions, one per dimension in theta:

T.visualize_gradient(theta)

Citations

This repository was presented at the International Conference of Machine Learning (ICML 2022).

@inproceedings{martinez2022closed,
    title={Closed-Form Diffeomorphic Transformations for Time Series Alignment},
    author={Martinez, I{\~n}igo and Viles, Elisabeth and Olaizola, Igor G},
    booktitle={International Conference on Machine Learning},
    pages={15122--15158},
    year={2022},
    organization={PMLR}
}

Furthermore, please cite previous articles by Freifeld et al. and Shapira Weber et al. that are essential to this work.

@article{freifeld2017transformations,
    title={Transformations based on continuous piecewise-affine velocity fields},
    author={Freifeld, Oren and Hauberg, S{\o}ren and Batmanghelich, Kayhan and Fisher, Jonn W},
    journal={IEEE transactions on pattern analysis and machine intelligence},
    volume={39},
    number={12},
    pages={2496--2509},
    year={2017},
    publisher={IEEE}
}

@inproceedings{freifeld2015highly,
    title={Highly-expressive spaces of well-behaved transformations: Keeping it simple},
    author={Freifeld, Oren and Hauberg, Soren and Batmanghelich, Kayhan and Fisher, John W},
    booktitle={Proceedings of the IEEE International Conference on Computer Vision},
    pages={2911--2919},
    year={2015}
}

@article{shapira2019diffeomorphic,
    title={Diffeomorphic temporal alignment nets},
    author={Shapira Weber, Ron A and Eyal, Matan and Skafte, Nicki and Shriki, Oren and Freifeld, Oren},
    journal={Advances in Neural Information Processing Systems},
    volume={32},
    year={2019}
}

Installation

As the compiled difw package is hosted on the Python Package Index (PyPI) you can easily install it with pip. To install difw, run this command in your terminal of choice:

$ pip install difw

or, alternatively:

$ python -m pip install difw

If you want to get difw's latest version, you can refer to the repository hosted at github:

python -m pip install https://github.com/imartinezl/difw/archive/master.zip

Environment Setup

Requirements

difw builds on numpy, torch, scipy, ninja, and matplotlib libraries.

Python 3

To find out which version of python you have, open a terminal window and try the following command:

$ python3 --version
Python 3.6.9

If you have python3 on your machine, then this command should respond with a version number. If you do not have python3 installed, follow these instructions.

Pip

pip is the reference Python package manager. It's used to install and update packages. In case pip is not installed in your OS, follow these procedure.

Virtual Environment

venv creates a “virtual” isolated Python installation and installs packages into that virtual installation. It is always recommended to use a virtual environment while developing Python applications. To create a virtual environment, go to your project’s directory and run venv.

$ python3 -m venv env

Before you can start installing or using packages in your virtual environment you'll need to activate it.

$ source env/bin/activate

Source Code

difw is developed on GitHub, where the code is always available.

You can either clone the public repository:

$ git clone git://github.com/imartinezl/difw.git

Or, download the tarball:

$ curl -OL https://github.com/imartinezl/difw/tarball/main
# optionally, zipball is also available (for Windows users).

Once you have a copy of the source, you can embed it in your own Python package, or install it into your site-packages easily:

$ cd difw
$ python -m pip install .