图(Graph):由顶点集合
$V$ 与边集合$E$ (顶点之间的关系)构成的数据结构。图的形式化定义为$G = (V, E)$ 。
-
顶点(Vertex):图中的基本元素,通常称为顶点,表示对象或节点。顶点的集合
$V$ 是有限非空集合,包含$n > 0$ 个顶点。如下面的示意图所示,通常我们使用圆圈来表示顶点。 -
边(Edge):顶点之间的关系或连接。边的形式化定义为:$e = \langle u, v \rangle$,表示从
$u$ 到$v$ 的一条边,其中$u$ 称为起始点,$v$ 称为终止点。如下面的示意图所示,通常我们使用连接两个顶点的线段来表示边。
-
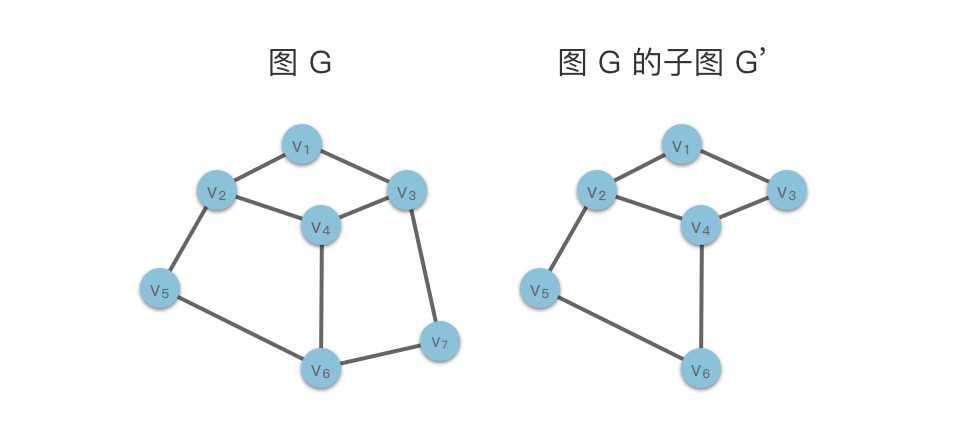
子图(Sub Graph):对于图
$G = (V, E)$ 与$G^{'} = (V^{'}, E^{'})$ ,如果满足$V^{'} \subseteq V$ ,$E^{'} \subseteq E$,则称图$G^{'}$ 是图$G$ 的一个子图。直观的说,子图是由原图的一部分顶点和边组成的,同时边的两端顶点必须属于子图的顶点集合$V^{'}$ 。特别地,根据定义,图$G$ 本身也是其一个子图。在下图中,我们展示了一个图$G$ 及其子图$G^{'}$ 。
根据边是否具有方向性,图可以分为两种类型:「无向图」和「有向图」。
无向图(Undirected Graph):如果图中每条边都没有方向性,则称为无向图。例如,表示朋友关系或者城市间双向行驶的路线图常用无向图建模。
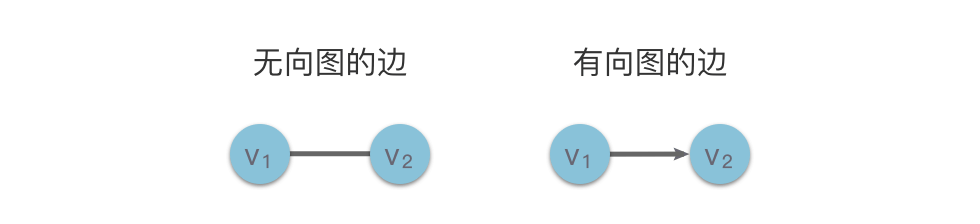
在无向图中,每条边都是由两个顶点组成的无序对。例如下图左侧中的顶点
有向图(Directed Graph):如果图中的每条边都具有方向性,则称为有向图。例如,表示任务流程的流程图或网络请求的依赖图是典型的有向图。
在有向图中,有向边(又称弧)是由两个顶点组成的有序对,例如下图右侧中从顶点
如果图中有
-
无向图中边的最大数量:在无向图中,任意两个顶点之间最多存在一条边,因此最多可以有
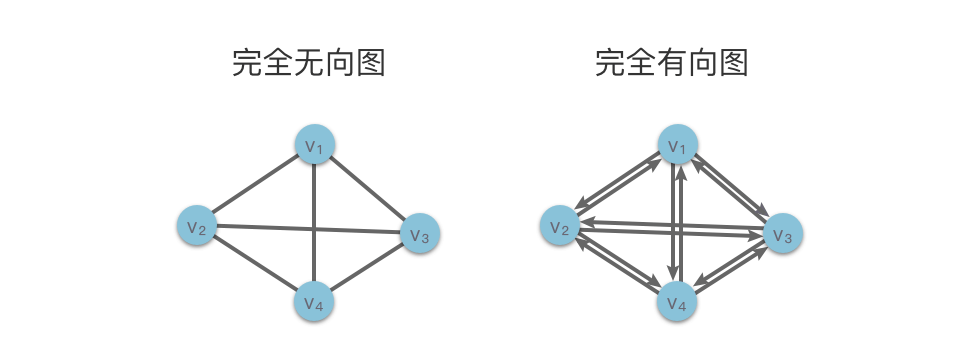
$\frac{n \times (n - 1)}{2}$ 条边。具有$\frac{n \times (n - 1)}{2}$ 条边的无向图称为 「完全无向图(Completed Undirected Graph)」。 -
有向图中边的最大数量:在有向图中,任意两个顶点之间可以存在一对方向相反的弧,因此最多可以有
$n \times (n - 1)$ 条弧。具有$n \times (n - 1)$ 条弧的有向图称为 「完全有向图(Completed Directed Graph)」。
下图展示了两个示例:左侧为包含
下面介绍一下无向图和有向图中一个重要概念 「顶点的度」。
顶点的度:与该顶点
$v_i$ 相关联的边的数量,记为$TD(v_i)$ 。
-
无向图中顶点的度:在无向图中,顶点的都是与该顶点相连的边的数量。例如,在上图左侧的完全无向图中,顶点
$v_3$ 的度为$3$ ,因为有$3$ 个其他的顶点与$v_3$ 相连接。 -
有向图中顶点的度:在有向图中,顶点的度可以分为「出度」和「入度」两个部分。
-
出度(Out Degree):以该顶点
$v_i$ 为出发点的边的条数,记为$OD(v_i)$ 。 -
入度(In Degree):以该顶点
$v_i$ 为终止点的边的条数,记为$ID(v_i)$ 。
-
出度(Out Degree):以该顶点
在有向图中,顶点
例如,在上图右侧的完全有向图中,顶点
路径 :图中的一个重要概念,对于图
$G = (V, E)$ ,如果存在顶点序列$v_{i_0}, v_{i_1}, v_{i_2}, …, v_{i_m}$ ,并且每对相邻的顶点都有图中的边连接,即$(v_{i_0}, v_{i_1}), (v_{i_1}, v_{i_2}), …, (v_{i_{m-1}}, v_{i_m}) \in E$ (对于有向图则是$\langle v_{i_0}, v_{i_1} \rangle, \langle v_{i_1}, v_{i_2} \rangle, …, \langle v_{i_{m-1}}, v_{i_m} \rangle \in E$ ),则称该顶点序列为从顶点$v_{i_0}$ 和顶点$v_{i_m}$ 之间的一条路径,其中$v_{i_0}$ 是这条路径的起始点,$v_{i_m}$ 是这条路径的终止点。
简而言之,如果顶点
-
环(Circle):如果一条路径的起始点和终止点相同(即
$v_{i_0} == v_{i_m}$ ),则称这条路径为「回路」或「环」。 -
简单路径:顶点序列中顶点不重复出现的路径称为「简单路径」。
根据图中是否有环,我们可以将图分为「环形图」和「无环图」。
- 环形图(Circular Graph):如果图中存在至少一条环路,则该图称为「环形图」。
- 无环图(Acyclic Graph):如果图中不存在环路,则该图称为「无环图」。
在有向图中,如果不存在环路,则将该图称为「有向无环图(Directed Acyclic Graph, DAG)」。有向无环图因其独特的拓扑结构,广泛应用于诸如动态规划、最短路径问题、数据压缩等算法场景。
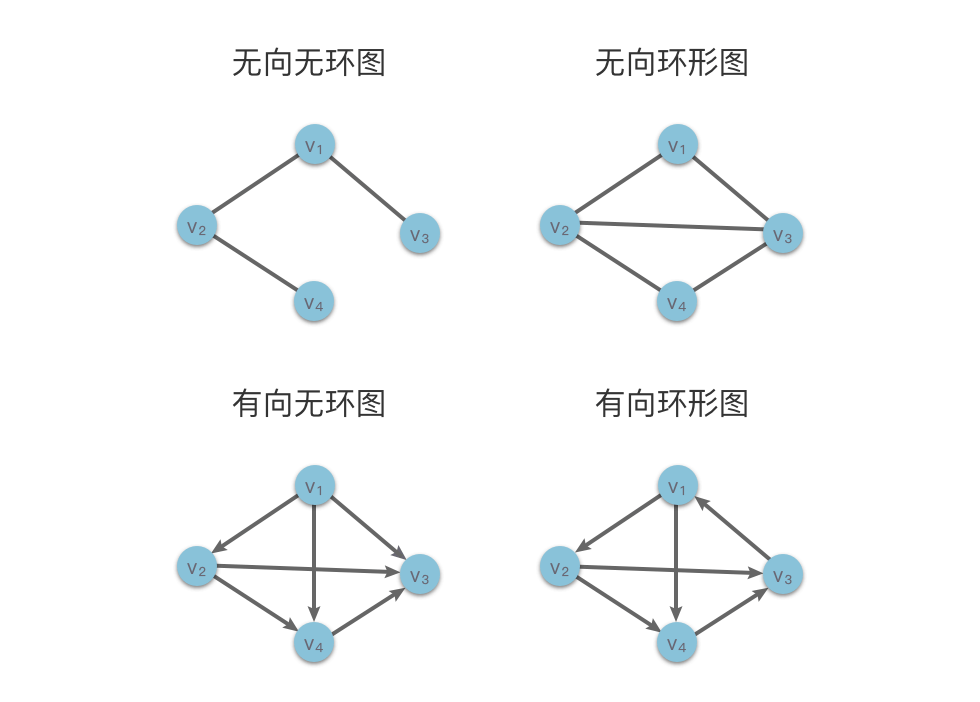
下图展示了四种图的类型:无向无环图、无向环形图、有向无环图和有向环形图。在有向环形图中,顶点
在无向图中,如果存在一条从顶点
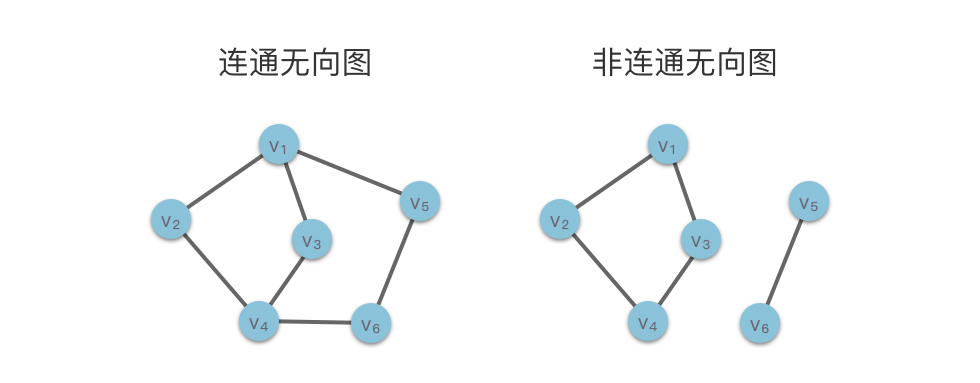
- 连通无向图:如果无向图中任意两个顶点之间都是连通的(即任意两个顶点之间都有路径连接),则称该图为「连通无向图」。
- 非连通无向图:如果无向图中存在至少一对顶点之间没有任何路径连接,则称该图为「非连通无向图」。
下图展示了两种情况:
- 在左侧图中,顶点
$v_1$ 与所有其他顶点$v_2$ 、$v_3$、$v_4$、$v_5$、$v_6$ 都是连通的,因此该图为连通无向图。 - 在右侧图中,顶点
$v_1$ 与$v_2$ 、$v_3$、$v_4$ 是连通的,但与$v_5$ 、$v_6$ 没有任何路径连接,因此该图为非连通无向图。
在无向图中,某些图可能不是连通的,但它们的子图可能是连通的。这样的子图称为「连通子图」。对于其中某个连通子图,如果不存在任何包含他的更大连通子图,则该连通子图称为「连通分量」。
- 连通子图:如果无向图的子图是连通的,则该子图称为连通子图。
- 连通分量:无向图中的一个极大连通子图(不存在任何包含它的更大的连通子图)称为该图的连通分量。
- 极⼤连通⼦图:无向图中的一个连通子图,且不存在包含它的更大的连通子图。
例如,上图右侧的非连通无向图中,尽管整体图是非连通的,但顶点
在有向图中,如果从顶点
-
强连通有向图:如果图中任意两个顶点
$v_i$ 和$v_j$ 都满足从$v_i$ 到$v_j$ 和从$v_j$ 到$v_i$ 均有路径,则称该图为「强连通有向图」。 - 非强连通有向图:如果图中存在至少一对顶点之间没有路径连接(即无法相互到达),则称该图为「非强连通有向图」。
下图展示了两种情况:
- 左侧图中,任意两个顶点之间都存在路径,因此该图为强连通有向图。
- 右侧图中,顶点
$v_7$ 无法通过路径到达其他顶点,因此该图为非强连通有向图。
在有向图中,「强联通分量」是指其内部任意两个顶点之间都强连通的极大强连通子图。以下是具体定义:
- 强连通子图:有向图的一个子图,且该子图中任意两个顶点都是强连通的。
- 极⼤强连通⼦图:如果一个强联通子图不能被包含在任何更大的强连通子图中,则称其为极大强连通子图。
- 强连通分量:有向图中的一个极⼤强连通⼦图,称为该图的强连通分量。
举个例子来解释一下。
例如,上图右侧的非强连通有向图,其本身不是强连通的(因为顶点
有时,图不仅需要表示顶点之间是否存在某种关系,还需要表示这一关系的具体细节。有时候我们需要给边赋予一些数据信息,这些数据信息被称为 权。在具体应用中,权值可以具有某种具体意义,比如权值可以代表距离、时间以及价格等不同属性。
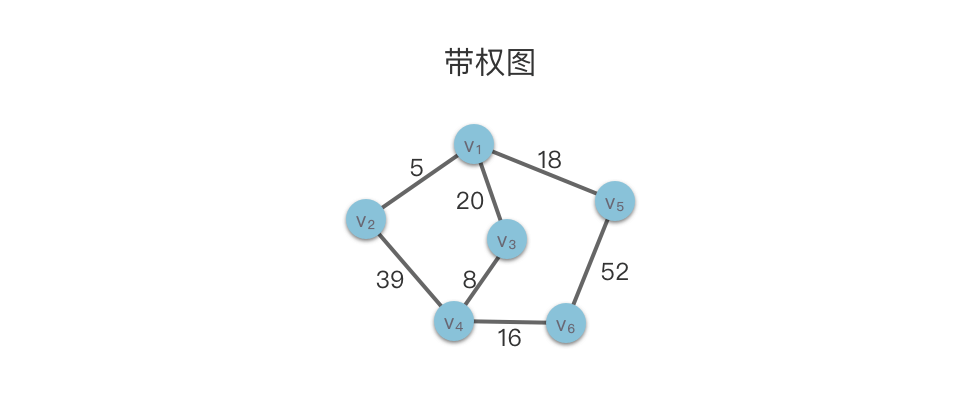
- 带权图:如果图的每条边都被赋以⼀个权值,则该图称为带权图。权值通常表示一个非负实数,但在某些场景下也可以是负数。
- 网络:带权的连通⽆向图被称为⽹络。
在下面的示意图中,我们给出了一个带权图的例子。
根据图中边的稀疏程度,我们可以将图分为「稠密图」和「稀疏图」。这是一个模糊的概念,目前为止还没有给出一个量化的定义。
-
稠密图(Dense Graph):有很多条边或弧(边的条数
$e$ 接近于完全图的边数)的图称为稠密图。 -
稀疏图(Sparse Graph):有很少条边或弧(边的条数
$e$ 远小于完全图的边数,如$e < n \times \log_2n$ )的图称为稀疏图。
- 【书籍】ACM-ICPC 程序设计系列 - 图论及应用 - 陈宇 吴昊 主编
- 【书籍】数据结构教程 第 3 版 - 唐发根 著
- 【书籍】大话数据结构 - 程杰 著
- 【书籍】算法训练营 - 陈小玉 著
- 【书籍】Python 数据结构与算法分析 第 2 版 - 布拉德利·米勒 戴维·拉努姆 著
- 【博文】图的基础知识 | 小浩算法
- 【博文】链式前向星及其简单应用 | Malash's Blog