1368. Minimum Cost to Make at Least One Valid Path in a Grid #1173
-
|
Topics: Given an
Notice that there could be some signs on the cells of the grid that point outside the grid. You will initially start at the upper left cell You can modify the sign on a cell with Return the minimum cost to make the grid have at least one valid path. Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We can use the 0-1 BFS approach. The idea is to traverse the grid using a deque (double-ended queue) where the cost of modifying the direction determines whether a cell is added to the front or back of the deque. The grid is treated as a graph where each cell has weighted edges based on whether its current direction matches the movement to its neighbors. Let's implement this solution in PHP: 1368. Minimum Cost to Make at Least One Valid Path in a Grid <?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function minCost($grid) {
$m = count($grid);
$n = count($grid[0]);
// Direction vectors for the signs (right, left, down, up)
$directions = [
[0, 1], // 1: right
[0, -1], // 2: left
[1, 0], // 3: down
[-1, 0] // 4: up
];
// Deque for 0-1 BFS
$deque = new SplQueue();
$deque->enqueue([0, 0, 0]); // [row, col, cost]
// Distance array to keep track of the minimum cost to reach each cell
$dist = array_fill(0, $m, array_fill(0, $n, PHP_INT_MAX));
$dist[0][0] = 0;
while (!$deque->isEmpty()) {
list($x, $y, $cost) = $deque->dequeue();
// If we've already found a better way, skip this cell
if ($dist[$x][$y] < $cost) {
continue;
}
// Traverse all 4 directions
foreach ($directions as $dirIndex => $dir) {
$nx = $x + $dir[0];
$ny = $y + $dir[1];
$newCost = $cost;
// Check if the new cell is within bounds
if ($nx >= 0 && $nx < $m && $ny >= 0 && $ny < $n) {
// If the direction of the current cell matches the intended movement
if ($grid[$x][$y] == $dirIndex + 1) {
$newCost = $cost; // No additional cost
} else {
$newCost = $cost + 1; // Modify the direction with cost 1
}
// Update distance and add to deque
if ($newCost < $dist[$nx][$ny]) {
$dist[$nx][$ny] = $newCost;
if ($newCost == $cost) {
$deque->unshift([$nx, $ny, $newCost]); // Add to front
} else {
$deque->enqueue([$nx, $ny, $newCost]); // Add to back
}
}
}
}
}
// Return the minimum cost to reach the bottom-right corner
return $dist[$m - 1][$n - 1];
}
// Example Test Cases
$grid1 = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]];
echo minCost($grid1) . "\n"; // Output: 3
$grid2 = [[1,1,3],[3,2,2],[1,1,4]];
echo minCost($grid2) . "\n"; // Output: 0
$grid3 = [[1,2],[4,3]];
echo minCost($grid3) . "\n"; // Output: 1
?>Explanation:
Complexity:
|
Beta Was this translation helpful? Give feedback.
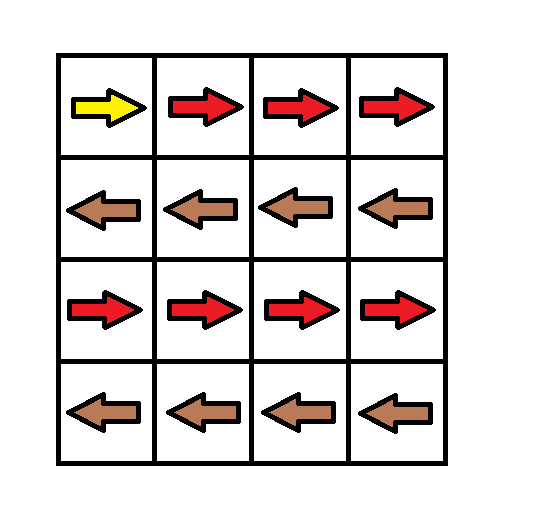
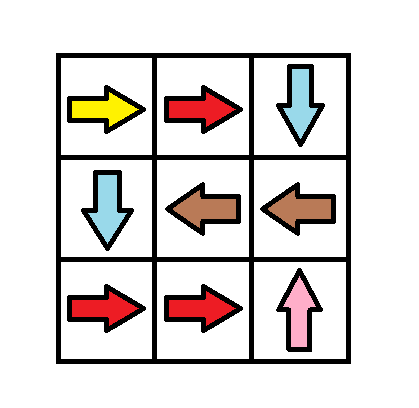
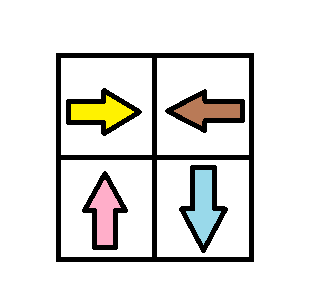
We can use the 0-1 BFS approach. The idea is to traverse the grid using a deque (double-ended queue) where the cost of modifying the direction determines whether a cell is added to the front or back of the deque. The grid is treated as a graph where each cell has weighted edges based on whether its current direction matches the movement to its neighbors.
Let's implement this solution in PHP: 1368. Minimum Cost to Make at Least One Valid Path in a Grid