2017. Grid Game #1191
-
|
Topics: You are given a 0-indexed 2D array Both robots initially start at At the start of the game, the first robot moves from The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot. Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We'll use the following approach:
Let's implement this solution in PHP: 2017. Grid Game <?php
function gridGame($grid) {
$n = count($grid[0]);
// Calculate prefix sums for both rows
$prefixTop = array_fill(0, $n + 1, 0);
$prefixBottom = array_fill(0, $n + 1, 0);
for ($i = 0; $i < $n; $i++) {
$prefixTop[$i + 1] = $prefixTop[$i] + $grid[0][$i];
$prefixBottom[$i + 1] = $prefixBottom[$i] + $grid[1][$i];
}
$minPointsForSecond = PHP_INT_MAX;
// Iterate over all possible transition points
for ($i = 0; $i < $n; $i++) {
// Points remaining in the top row after $i
$topRemaining = $prefixTop[$n] - $prefixTop[$i + 1];
// Points remaining in the bottom row before $i
$bottomRemaining = $prefixBottom[$i];
// Maximum points the second robot can collect
$secondRobotPoints = max($topRemaining, $bottomRemaining);
// Minimize the maximum points for the second robot
$minPointsForSecond = min($minPointsForSecond, $secondRobotPoints);
}
return $minPointsForSecond;
}
// Example usage
$grid1 = [[2, 5, 4], [1, 5, 1]];
$grid2 = [[3, 3, 1], [8, 5, 2]];
$grid3 = [[1, 3, 1, 15], [1, 3, 3, 1]];
echo gridGame($grid1) . "\n"; // Output: 4
echo gridGame($grid2) . "\n"; // Output: 4
echo gridGame($grid3) . "\n"; // Output: 7
?>Explanation:
Example WalkthroughInput:
|
Beta Was this translation helpful? Give feedback.
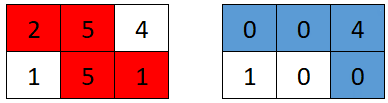
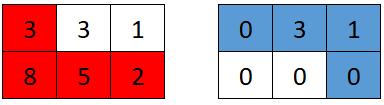
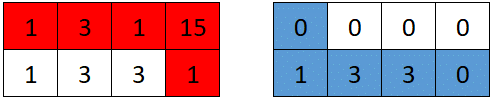
We'll use the following approach:
Prefix Sum Calculation: We'll compute the prefix sums for both rows of the grid to efficiently calculate the sum of points for any subarray.
Simulating Optimal Movement:
Minimizing the Maximum Points for the Second Robot: