979. Distribute Coins in Binary Tree

[mah-shamim]

Topics: Tree, Depth-First Search, Binary Tree

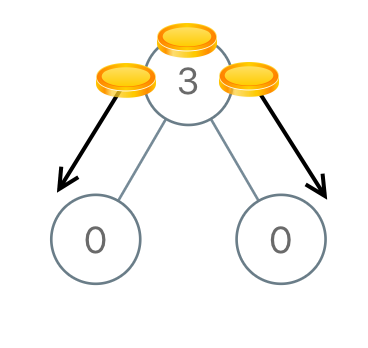
You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

Example 1:

• Input: root = [3,0,0]
• Output: 2
• Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

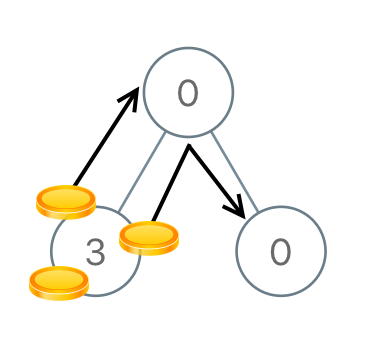
Example 2:

• Input: oot = [0,3,0]
• Output: 3
• Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Constraints:

• The number of nodes in the tree is n.
• 1 <= n <= 100
• 0 <= Node.val <= n
• The sum of all Node.val is n.

[mah-shamim]

The problem requires redistributing coins in a binary tree such that each node ends up with exactly one coin. You are given a binary tree with n nodes, where each node contains a certain number of coins. The goal is to determine the minimum number of moves needed to ensure every node has exactly one coin. A move consists of transferring a coin between adjacent nodes, either from a parent to a child or vice versa.

Key Points

1. Tree structure: A binary tree is given with n nodes.
2. Node coins: Each node may have a number of coins.
3. Moves: A move consists of transferring one coin between adjacent nodes.
4. Objective: Minimize the number of moves to ensure each node has exactly one coin.

Approach

The key to solving this problem lies in using Depth First Search (DFS) to traverse the binary tree and balance the coins. We aim to track the number of excess coins at each node and ensure that excess coins are moved to nodes that have fewer than one coin. Here's how to approach the problem:

1. DFS Traversal: Traverse the tree starting from the leaves up to the root. For each node, we calculate how many coins need to be moved.
2. Excess Coins: For each node, if it has more coins than required, it will pass the excess coins to its parent or child nodes. If it has fewer coins, it will receive coins from its child or parent.
3. Total Moves: The total number of moves is the sum of the absolute number of excess coins moved for each node.

Plan

1. Use DFS to traverse the tree.
2. For each node, calculate how many moves are required to balance its left and right subtrees.
3. At each node, count how many coins need to be moved up to the parent or down to the children.
4. Accumulate the total moves as we traverse the tree.
5. Return the accumulated total moves.

Let's implement this solution in PHP: 979. Distribute Coins in Binary Tree

<?php
/**
 * @param TreeNode $root
 * @return Integer
 */
function distributeCoins(TreeNode $root): int
{
    $totalMoves = 0; // This will store the total number of moves needed to balance the coins

    // The Depth First Search (DFS) function computes the number of moves required
    // starting from the leaves up to the root of the tree.
    // It returns the excess number of coins that need to be moved from the current node.

    $dfs = function($node) use (&$dfs, &$totalMoves) {

        // Base case: if the current node is null, return 0 since there are no coins to move.
        if (!$node) {
            return 0;
        }

        // Recursive case: solve for left and right subtrees.
        $leftMoves = $dfs($node->left);
        $rightMoves = $dfs($node->right);

        // The number of moves made at the current node is the sum of absolute values of each subtree’s excess coins.
        // Because moves from both left and right need to pass through the current node.
        $totalMoves += abs($leftMoves) + abs($rightMoves);

        // Return the number of excess coins at this node: positive if there are more coins than nodes,
        // negative if there are fewer. A value of -1 means just the right amount for the node itself.
        return $leftMoves + $rightMoves + $node->val - 1;
    };

    // Call the DFS function starting from the root of the tree.
    $dfs($root);

    // Return the total number of moves needed to distribute the coins.
    return $totalMoves;
}

// Example 1
$root = [3,0,0];
echo distributeCoins($root);  // Output: 2

// Example 2
$root = [0,3,0];
echo distributeCoins($root);  // Output: 3
?>

1. DFS Function: It recursively calculates the excess coins for each node. For each subtree, it moves excess coins up or down to balance the tree.
2. Base Case: If a node is null, it returns 0 because there are no coins to redistribute.
3. Recursive Case: The function calculates moves for both left and right children and updates the total move count.

Explanation:

1. DFS Function: This function will return the total number of excess coins at a node and will accumulate the number of moves. The excess coins at each node will be the difference between the node's coin count and 1 (the required number of coins for each node). If the node has excess coins (i.e., more than one), those coins will be passed up or down to other nodes, and the moves are counted.

2. Returning Excess Coins: The excess coins for a node are the sum of the excess coins in its left and right subtrees, plus the number of coins in the current node minus one (since each node needs exactly one coin).

3. Result: The total number of moves is the sum of absolute values of the excess coins at each node, because every excess coin needs to be moved.

Example Walkthrough

Example 1:
Tree: [3,0,0]

    3
   / \
  0   0

• Root node has 3 coins, and each child node has 0 coins.
• We need to move 1 coin from the root to its left child, and 1 coin to its right child.
• Thus, 2 moves are required.

Example 2:
Tree: [0,3,0]

    0
   / \
  3   0

• The left child has 3 coins, which is too many. It moves 2 coins to the root.
• The root then moves 1 coin to the right child.
• This requires 3 moves in total.

Time Complexity

• The algorithm visits each node once during the DFS traversal, so the time complexity is O(n), where n is the number of nodes in the tree.

Output for Example

• Example 1:
  Input: [3,0,0]
  Output: 2

• Example 2:
  Input: [0,3,0]
  Output: 3

This problem can be efficiently solved using Depth First Search (DFS). By calculating the excess coins for each node and accumulating the required moves, we can determine the minimum number of moves to redistribute the coins such that every node has exactly one. The approach is optimal with a time complexity of O(n), making it suitable for trees with up to 100 nodes.

[basharul-siddike]

Thanks to solution for the "Distribute Coins in Binary Tree" problem

[mah-shamim]

Thanks