1514. Path with Maximum Probability

[mah-shamim]

Topics: Array, Graph, Heap (Priority Queue), Shortest Path

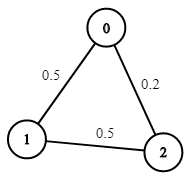
You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Example 1:

• Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
• Output: 0.25000
• Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

• Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
• Output: 0.30000

Example 3:

• Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
• Output: 0.00000
• Explanation: There is no path between 0 and 2.

Constraints:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes

Hint:

1. Multiplying probabilities will result in precision errors.
2. Take log probabilities to sum up numbers instead of multiplying them.
3. Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs.

[topugit]

We can use a modified version of Dijkstra's algorithm. Instead of finding the shortest path, you'll be maximizing the probability of success.

Let's implement this solution in PHP: 1514. Path with Maximum Probability

<?php
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
    // Create an adjacency list to represent the graph
    $graph = array_fill(0, $n, []);
    foreach ($edges as $i => $edge) {
        list($a, $b) = $edge;
        $graph[$a][] = [$b, $succProb[$i]];
        $graph[$b][] = [$a, $succProb[$i]];
    }

    // Initialize the maximum probabilities array
    $maxProb = array_fill(0, $n, 0.0);
    $maxProb[$start_node] = 1.0;

    // Use a max heap (priority queue) to explore the paths
    $pq = new SplPriorityQueue();
    $pq->insert([$start_node, 1.0], 1.0);

    // Dijkstra's algorithm to find the path with maximum probability
    while (!$pq->isEmpty()) {
        list($node, $prob) = $pq->extract();

        // If we reached the end node, return the probability
        if ($node == $end_node) {
            return $prob;
        }

        // Explore the neighbors
        foreach ($graph[$node] as $neighbor) {
            list($nextNode, $edgeProb) = $neighbor;
            $newProb = $prob * $edgeProb;
            if ($newProb > $maxProb[$nextNode]) {
                $maxProb[$nextNode] = $newProb;
                $pq->insert([$nextNode, $newProb], $newProb);
            }
        }
    }

    // If no path was found, return 0
    return 0.0;
}

// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;

echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000


$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;

echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000


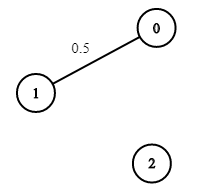
$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;

echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>

Explanation:

1. Graph Representation: The graph is represented as an adjacency list where each node points to its neighbors along with the success probabilities of the edges connecting them.

2. Max Probability Array: An array maxProb is used to store the maximum probability to reach each node from the start node.

3. Priority Queue: A max heap (SplPriorityQueue) is used to explore paths with the highest probability first. This is crucial to ensure that when we reach the destination node, we've found the path with the maximum probability.

4. Algorithm:

   • Initialize the start node's probability as 1 (since the probability of staying at the start is 1).
   • Use the priority queue to explore nodes, updating the maximum probability to reach each neighbor.
   • If the destination node is reached, return the probability.
   • If no path exists, return 0.

Output:

For the example provided:

$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;

The output will be 0.25.

This approach ensures an efficient solution using Dijkstra's algorithm while handling the specifics of probability calculations.

[mah-shamim]

Thanks to solve the 'Path with Maximum Probability' problem

[topugit]

Thnaks