2699. Modify Graph Edge Weights #436
-
|
Topics: You are given an undirected weighted connected graph containing Some edges have a weight of Your task is to modify all edges with a weight of Return an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from Note: You are not allowed to modify the weights of edges with initial positive weights. Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We can break down the approach as follows: Approach:
Let's implement this solution in PHP: 2699. Modify Graph Edge Weights <?php
private $kMax = 2000000000;
/**
* @param $n
* @param $edges
* @param $source
* @param $destination
* @param $target
* @return array|mixed
*/
function modifiedGraphEdges($n, $edges, $source, $destination, $target) {
$graph = array_fill(0, $n, []);
// Build the graph
foreach ($edges as $edge) {
list($u, $v, $w) = $edge;
if ($w == -1) continue;
$graph[$u][] = [$v, $w];
$graph[$v][] = [$u, $w];
}
// Calculate distance from source to destination
$distToDestination = dijkstra($graph, $source, $destination);
if ($distToDestination < $target) return [];
if ($distToDestination == $target) {
// Change the weights of negative edges to an impossible value
foreach ($edges as &$edge) {
if ($edge[2] == -1) {
$edge[2] = $this->kMax;
}
}
return $edges;
}
// Modify the graph and adjust weights
for ($i = 0; $i < count($edges); ++$i) {
list($u, $v, $w) = $edges[$i];
if ($w != -1) continue;
$edges[$i][2] = 1;
$graph[$u][] = [$v, 1];
$graph[$v][] = [$u, 1];
$distToDestination = dijkstra($graph, $source, $destination);
if ($distToDestination <= $target) {
$edges[$i][2] += $target - $distToDestination;
// Change the weights of negative edges to an impossible value
for ($j = $i + 1; $j < count($edges); ++$j) {
if ($edges[$j][2] == -1) {
$edges[$j][2] = $this->kMax;
}
}
return $edges;
}
}
return [];
}
/**
* @param $graph
* @param $src
* @param $dst
* @return int|mixed
*/
function dijkstra($graph, $src, $dst) {
$dist = array_fill(0, count($graph), PHP_INT_MAX);
$minHeap = new SplPriorityQueue();
$minHeap->setExtractFlags(SplPriorityQueue::EXTR_BOTH);
$dist[$src] = 0;
$minHeap->insert($src, 0);
while (!$minHeap->isEmpty()) {
$node = $minHeap->extract();
$u = $node['data'];
$d = -$node['priority'];
if ($d > $dist[$u]) continue;
foreach ($graph[$u] as list($v, $w)) {
if ($d + $w < $dist[$v]) {
$dist[$v] = $d + $w;
$minHeap->insert($v, -$dist[$v]);
}
}
}
return $dist[$dst];
}
// Example usage:
// Example 1
$n = 5;
$edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]];
$source = 0;
$destination = 1;
$target = 5;
print_r(modifyGraphEdgeWeights($n, $edges, $source, $destination, $target)); // Output: [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
// Example 2
$n = 3;
$edges = [[0,1,-1],[0,2,5]];
$source = 0;
$destination = 2;
$target = 6;
print_r(modifyGraphEdgeWeights($n, $edges, $source, $destination, $target)); // Output: []
// Example 3
$n = 4;
$edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]];
$source = 0;
$destination = 2;
$target = 6;
print_r(modifyGraphEdgeWeights($n, $edges, $source, $destination, $target)); // Output: [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
?>Explanation:
This approach efficiently checks and adjusts edge weights, ensuring that the target distance is met if possible. |
Beta Was this translation helpful? Give feedback.
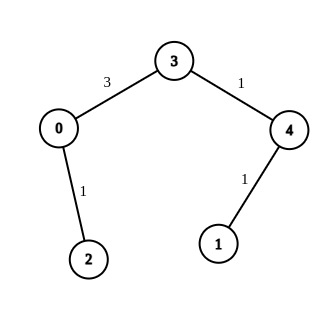
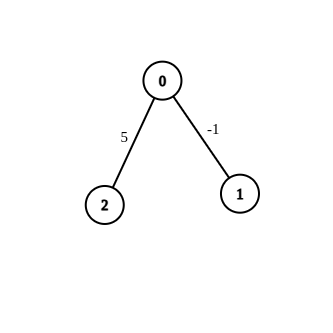
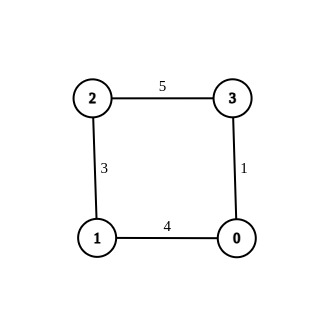
We can break down the approach as follows:
Approach:
Initial Check with Existing Weights:
sourcetodestinationusing only the edges with positive weights, ignoring the edges with weight-1.target, then it's impossible to modify the-1edges to achieve the target, so we return an empty array.Temporary Assignment of Weight 1:
1to all edges with weight-1and recompute the shortest path.target, then it's impossible to achieve the target, so we return an empty array.Modify Specific Edge Weights: