2641. Cousins in Binary Tree II

[mah-shamim]

Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree

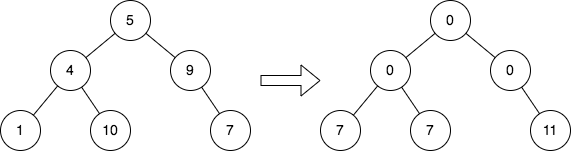
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

• Input: root = [5,4,9,1,10,null,7]
• Output: [0,0,0,7,7,null,11]
• Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
  • Node with value 5 does not have any cousins so its sum is 0.
  • Node with value 4 does not have any cousins so its sum is 0.
  • Node with value 9 does not have any cousins so its sum is 0.
  • Node with value 1 has a cousin with value 7 so its sum is 7.
  • Node with value 10 has a cousin with value 7 so its sum is 7.
  • Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

• Input: root = [3,1,2]
• Output: [0,0,0]
• Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
  • Node with value 3 does not have any cousins so its sum is 0.
  • Node with value 1 does not have any cousins so its sum is 0.
  • Node with value 2 does not have any cousins so its sum is 0.

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 104

Hint:

1. Use DFS two times.
2. For the first time, find the sum of values of all the levels of the binary tree.
3. For the second time, update the value of the node with the sum of the values of the current level - sibling node’s values.

[kovatz]

The solution uses a Depth-First Search (DFS) approach twice:

1. First DFS: Calculate the sum of all node values at each level of the tree.
2. Second DFS: Update each node's value with the sum of its cousins' values by subtracting its siblings' values from the total for that level.

Let's implement this solution in PHP: 2641. Cousins in Binary Tree II

<?php
// Definition for a binary tree node.
class TreeNode {
    public $val = null;
    public $left = null;
    public $right = null;
    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {

    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function replaceValueInTree($root) {
        $levelSums = [];
        $this->dfs($root, 0, $levelSums);
        return $this->replace($root, 0, new TreeNode(0), $levelSums);
    }

    /**
     * DFS to calculate the sum of node values at each level.
     * @param $root - current node
     * @param $level - current depth level in the tree
     * @param $levelSums - array holding the sum of values at each level
     * @return void
     */
    private function dfs($root, $level, &$levelSums) {
        if ($root === null) {
            return;
        }

        if (count($levelSums) == $level) {
            $levelSums[] = 0; // Initialize the sum for this level
        }

        $levelSums[$level] += $root->val; // Add current node's value to level sum

        // Recursive DFS calls for left and right children
        $this->dfs($root->left, $level + 1, $levelSums);
        $this->dfs($root->right, $level + 1, $levelSums);
    }

    /**
     * DFS to replace the node values with the sum of cousins' values.
     * @param $root - current node in the original tree
     * @param $level - current depth level in the tree
     * @param $curr - node being modified in the new tree
     * @param $levelSums - array holding the sum of values at each level
     * @return mixed
     */
    private function replace($root, $level, $curr, $levelSums) {
        $nextLevel = $level + 1;

        // Calculate the sum of cousins' values
        $nextLevelCousinsSum = ($nextLevel >= count($levelSums)) ? 0 :
            $levelSums[$nextLevel] -
            (($root->left === null) ? 0 : $root->left->val) -
            (($root->right === null) ? 0 : $root->right->val);

        // Update left child if it exists
        if ($root->left !== null) {
            $curr->left = new TreeNode($nextLevelCousinsSum);
            $this->replace($root->left, $level + 1, $curr->left, $levelSums);
        }

        // Update right child if it exists
        if ($root->right !== null) {
            $curr->right = new TreeNode($nextLevelCousinsSum);
            $this->replace($root->right, $level + 1, $curr->right, $levelSums);
        }

        return $curr;
    }
}

// Helper function to print the tree (for testing purpose)
function printTree($root) {
    if ($root === null) return [];
    
    $result = [];
    $queue = [$root];
    
    while (!empty($queue)) {
        $node = array_shift($queue);
        if ($node !== null) {
            $result[] = $node->val;
            $queue[] = $node->left;
            $queue[] = $node->right;
        } else {
            $result[] = null;
        }
    }
    
    // Remove trailing null values for clean output
    while (end($result) === null) {
        array_pop($result);
    }
    
    return $result;
}

// Example usage:

// Tree: [5,4,9,1,10,null,7]
$root = new TreeNode(5);
$root->left = new TreeNode(4);
$root->right = new TreeNode(9);
$root->left->left = new TreeNode(1);
$root->left->right = new TreeNode(10);
$root->right->right = new TreeNode(7);

$solution = new Solution();
$modifiedTree = $solution->replaceValueInTree($root);

print_r(printTree($modifiedTree));  // Output: [0, 0, 0, 7, 7, null, 11]
?>

Breakdown of the Code

1. replaceValueInTree Method

• This is the main method that initializes the process.
• It creates an empty array, $levelSums, to hold the sum of values at each level.
• It calls the first DFS to populate $levelSums and then calls the second DFS to replace the values in the tree.

2. dfs Method (First DFS)

• Parameters:

  • $root: Current node.
  • $level: Current depth level of the tree.
  • &$levelSums: Reference to the array where sums will be stored.

• Base Case: If the node is null, return.

• If the current level's sum is not initialized (i.e., the level does not exist in the array), initialize it to 0.

• Add the current node's value to the sum for its level.

• Recursively call dfs for the left and right children, incrementing the level by 1.

3. replace Method (Second DFS)

• Parameters:

  • $root: Current node.
  • $level: Current depth level.
  • $curr: Current node in the modified tree.
  • $levelSums: The array with sums for each level.

• Calculate the sum of cousins' values:

  • Get the total sum for the next level.
  • Subtract the values of the current node's children (siblings) from this total to get the cousins' sum.

• If the left child exists, create a new TreeNode with the cousins' sum and recursively call replace for it.

• If the right child exists, do the same for the right child.

Example Walkthrough

Let's use the first example from the prompt:

Input

root = [5,4,9,1,10,null,7]

1. First DFS (Calculate Level Sums):

   • Level 0: 5 → Sum = 5
   • Level 1: 4 + 9 → Sum = 13
   • Level 2: 1 + 10 + 7 → Sum = 18
   • Final levelSums: [5, 13, 18]

2. Second DFS (Replace Values):

   • At Level 0: 5 has no cousins → Replace with 0.
   • At Level 1:
     • 4 → Cousins = 9 → Replace with 9 (from Level 1 total, no siblings).
     • 9 → Cousins = 4 → Replace with 4.
   • At Level 2:
     • 1 → Cousins = 10 + 7 = 17 → Replace with 17.
     • 10 → Cousins = 1 + 7 = 8 → Replace with 8.
     • 7 → Cousins = 1 + 10 = 11 → Replace with 11.

Output

Output: [0, 0, 0, 7, 7, null, 11]

This step-by-step replacement based on cousin values results in the modified tree as shown in the example.

Summary

• The solution uses two DFS traversals: one for calculating the sums and the other for replacing node values.
• The logic ensures each node is updated based on its cousin nodes' values while maintaining the structure of the binary tree.

[mah-shamim]

Thanks to solve the "Cousins in Binary Tree II" problem

[kovatz]

Thanks