2458. Height of Binary Tree After Subtree Removal Queries

[mah-shamim]

Topics: Array, Tree, Depth-First Search, Breadth-First Search, Binary Tree

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

• Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
• Output: [2]
• Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
  The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

• Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
• Output: [3,2,3,2]
• Explanation: We have the following queries:
  • Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
  • Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
  • Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
  • Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

Hint:

1. Try pre-computing the answer for each node from 1 to n, and answer each query in O(1).
2. The answers can be precomputed in a single tree traversal after computing the height of each subtree.

[kovatz]

The solution employs a two-pass approach:

1. Calculate the height of each node in the tree.
2. Determine the maximum height of the tree after removing the subtree rooted at each queried node.

Code Breakdown

1. Class Definition and Properties:

class Solution {

    private $valToMaxHeight = [];
    private $valToHeight = [];

• valToMaxHeight: This array will store the maximum height of the tree after removing each node's subtree.
• valToHeight: This array will store the height of each node's subtree.

2. Main Function:

function treeQueries($root, $queries) {
    $this->height($root);
    $this->dfs($root, 0, 0);

    $answer = [];
    foreach ($queries as $query) {
        $answer[] = $this->valToMaxHeight[$query];
    }

    return $answer;
}

• The function treeQueries takes the root of the tree and the queries array.
• It first calls the height function to compute the height of each node.
• Then, it calls the dfs (depth-first search) function to compute the maximum heights after subtree removals.
• Finally, it populates the answer array with the results for each query.

3. Height Calculation:

private function height($node) {
    if ($node === null) {
        return 0;
    }

    if (isset($this->valToHeight[$node->val])) {
        return $this->valToHeight[$node->val];
    }

    $leftHeight = $this->height($node->left);
    $rightHeight = $this->height($node->right);

    $this->valToHeight[$node->val] = 1 + max($leftHeight, $rightHeight);
    return $this->valToHeight[$node->val];
}

• This function computes the height of each node recursively.
• If the node is null, it returns 0.
• If the height of the node is already computed, it retrieves it from the cache (valToHeight).
• It calculates the height based on the heights of its left and right children and stores it in valToHeight.

4. Depth-First Search for Maximum Height:

private function dfs($node, $depth, $maxHeight) {
    if ($node === null) {
        return;
    }

    $this->valToMaxHeight[$node->val] = $maxHeight;

    // Update heights for left and right subtree
    $leftHeight = isset($this->valToHeight[$node->right->val]) ? $this->valToHeight[$node->right->val] : 0;
    $rightHeight = isset($this->valToHeight[$node->left->val]) ? $this->valToHeight[$node->left->val] : 0;

    // Recursive DFS call for left and right subtrees
    $this->dfs($node->left, $depth + 1, max($maxHeight, $depth + $leftHeight));
    $this->dfs($node->right, $depth + 1, max($maxHeight, $depth + $rightHeight));
}

• This function performs a DFS to compute the maximum height of the tree after each node's subtree is removed.
• It records the current maximum height in valToMaxHeight for the current node.
• It calculates the heights of the left and right subtrees and updates the maximum height accordingly.
• It recursively calls itself for the left and right children, updating the depth and maximum height.

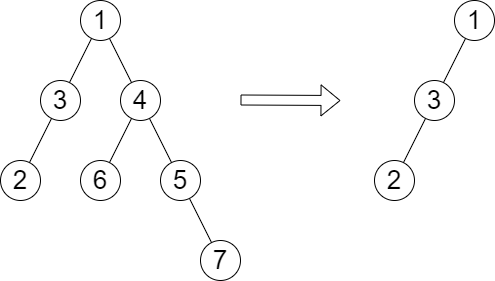
Example Walkthrough

Let's go through an example step-by-step.

Example Input:

// Tree Structure
//        1
//       / \
//      3   4
//     /   / \
//    2   6   5
//         \
//          7

$root = [1, 3, 4, 2, null, 6, 5, null, null, null, null, null, 7];
$queries = [4];

Initial Height Calculation:

• The height of the tree rooted at 1: 3
• The height of the tree rooted at 3: 2
• The height of the tree rooted at 4: 2 (height of subtrees rooted at 6 and 5)
• The height of the tree rooted at 6: 1 (just node 7)
• The height of the tree rooted at 2: 0 (leaf node)

After the height computation, valToHeight would look like this:

$valToHeight = [
    1 => 3,
    2 => 0,
    3 => 2,
    4 => 2,
    5 => 0,
    6 => 1,
    7 => 0
];

DFS for Max Heights:

• For the root (1), removing subtree 4 leaves:
  • Left Height: 2 (rooted at 3)
  • Right Height: 1 (rooted at 5)
• Thus, the maximum height after removing 4 is 2.

Result Array After Queries:

• For the query 4, the result would be [2].

Final Output

The result for the input provided will be:

// Output
[2]

This structured approach ensures that we efficiently compute the necessary heights and answer each query in constant time after the initial preprocessing. The overall complexity is O(n + m), where n is the number of nodes in the tree and m is the number of queries.

[mah-shamim]

Thanks to solution for the problem "Height of Binary Tree After Subtree Removal Queries," explaining each part of the code and the logic behind it with examples

[kovatz]

Thanks