1975. Maximum Matrix Sum #871
-
|
Topics: You are given an
Two elements are considered adjacent if and only if they share a border. Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to minimize the absolute value of the negative contributions to the sum. Here's the plan:
Let's implement this solution in PHP: 1975. Maximum Matrix Sum <?php
/**
* @param Integer[][] $matrix
* @return Integer
*/
function maximumMatrixSum($matrix) {
$n = count($matrix);
$sum = 0;
$minAbs = PHP_INT_MAX;
$negativeCount = 0;
// Iterate through the matrix
for ($i = 0; $i < $n; $i++) {
for ($j = 0; $j < $n; $j++) {
$sum += abs($matrix[$i][$j]);
$minAbs = min($minAbs, abs($matrix[$i][$j]));
if ($matrix[$i][$j] < 0) {
$negativeCount++;
}
}
}
// If there is an odd number of negatives, subtract twice the smallest absolute value
if ($negativeCount % 2 != 0) {
$sum -= 2 * $minAbs;
}
return $sum;
}
// Test case 1
$matrix1 = [[1, -1], [-1, 1]];
echo "Output: " . maximumMatrixSum($matrix1) . "\n"; // Output: 4
// Test case 2
$matrix2 = [[1, 2, 3], [-1, -2, -3], [1, 2, 3]];
echo "Output: " . maximumMatrixSum($matrix2) . "\n"; // Output: 16
?>Explanation:
Complexity
This solution works efficiently within the given constraints. |
Beta Was this translation helpful? Give feedback.
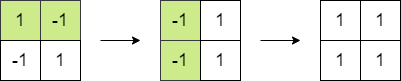
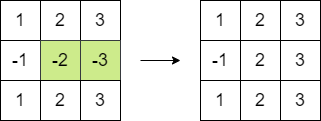
We need to minimize the absolute value of the negative contributions to the sum. Here's the plan:
Let's implement this solution in PHP: 1975. Maximum Matrix Sum