2290. Minimum Obstacle Removal to Reach Corner

[mah-shamim]

Topics: Array, Breadth-First Search, Graph, Heap (Priority Queue), Matrix, Shortest Path

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

• 0 represents an empty cell,
• 1 represents an obstacle that may be removed.

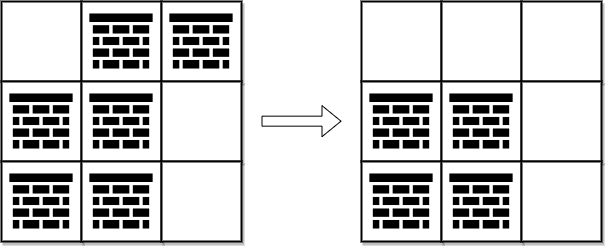
You can move up, down, left, or right from and to an empty cell.

Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).

Example 1:

• Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
• Output: 2
• Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
  It can be shown that we need to remove at least 2 obstacles, so we return 2.
  Note that there may be other ways to remove 2 obstacles to create a path.

Example 2:

• Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
• Output: 0
• Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 2 <= m * n <= 105
• grid[i][j] is either 0 or 1.
• grid[0][0] == grid[m - 1][n - 1] == 0

Hint:

1. Model the grid as a graph where cells are nodes and edges are between adjacent cells. Edges to cells with obstacles have a cost of 1 and all other edges have a cost of 0.
2. Could you use 0-1 Breadth-First Search or Dijkstra’s algorithm?

[mah-shamim]

We need to model this problem using a graph where each cell in the grid is a node. The goal is to navigate from the top-left corner (0, 0) to the bottom-right corner (m-1, n-1), while minimizing the number of obstacles (1s) we need to remove.

Approach:

1. Graph Representation:

   • Each cell in the grid is a node.
   • Movement between adjacent cells (up, down, left, right) is treated as an edge.
   • If an edge moves through a cell with a 1 (obstacle), the cost is 1 (remove the obstacle), and if it moves through a 0 (empty cell), the cost is 0.

2. Algorithm Choice:

   • Since we need to minimize the number of obstacles removed, we can use 0-1 BFS (Breadth-First Search with a deque) or Dijkstra's algorithm with a priority queue.
   • 0-1 BFS is suitable here because each edge has a cost of either 0 or 1.

3. 0-1 BFS:

   • We use a deque (double-ended queue) to process nodes with different costs:
     • Push cells with cost 0 to the front of the deque.
     • Push cells with cost 1 to the back of the deque.
   • The idea is to explore the grid and always expand the path that does not require obstacle removal first, and only remove obstacles when necessary.

Let's implement this solution in PHP: 2290. Minimum Obstacle Removal to Reach Corner

<?php
/**
 * @param Integer[][] $grid
 * @return Integer
 */
function minimumObstacles($grid) {
    $rows = count($grid);
    $cols = count($grid[0]);
    
    // Directions for moving up, down, left, right
    $directions = [[0, 1], [1, 0], [0, -1], [-1, 0]];
    
    // Deque for 0-1 BFS
    $deque = new SplDoublyLinkedList();
    $deque->push([0, 0, 0]); // [row, col, cost]
    
    // Visited array
    $visited = array_fill(0, $rows, array_fill(0, $cols, false));
    $visited[0][0] = true;
    
    // 0-1 BFS
    while (!$deque->isEmpty()) {
        list($x, $y, $cost) = $deque->shift();
        
        // If we reach the bottom-right corner, return the cost
        if ($x == $rows - 1 && $y == $cols - 1) {
            return $cost;
        }
        
        // Explore neighbors
        foreach ($directions as $direction) {
            $nx = $x + $direction[0];
            $ny = $y + $direction[1];
            
            // Check if the new position is within bounds and not visited
            if ($nx >= 0 && $nx < $rows && $ny >= 0 && $ny < $cols && !$visited[$nx][$ny]) {
                $visited[$nx][$ny] = true;
                
                // If no obstacle, add to the front of the deque
                if ($grid[$nx][$ny] == 0) {
                    $deque->unshift([$nx, $ny, $cost]);
                } else {
                    // If obstacle, add to the back of the deque
                    $deque->push([$nx, $ny, $cost + 1]);
                }
            }
        }
    }
    
    return -1; // Should not reach here if there's a valid path
}

// Test Case 1
$grid1 = [
    [0, 1, 1],
    [1, 1, 0],
    [1, 1, 0]
];
echo minimumObstacles($grid1) . PHP_EOL; // Output: 2

// Test Case 2
$grid2 = [
    [0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0]
];
echo minimumObstacles($grid2) . PHP_EOL; // Output: 0
?>

Explanation:

1. Input Parsing:

   • The grid is taken as a 2D array.
   • Rows and columns are calculated for bounds checking.

2. Deque Implementation:

   • SplDoublyLinkedList is used to simulate the deque. It supports adding elements at the front (unshift) or the back (push).

3. Visited Array:

   • Keeps track of cells already visited to avoid redundant processing.

4. 0-1 BFS Logic:

   • Start from (0, 0) with a cost of 0.
   • For each neighboring cell:
     • If it's empty (grid[nx][ny] == 0), add it to the front of the deque with the same cost.
     • If it's an obstacle (grid[nx][ny] == 1), add it to the back of the deque with an incremented cost.

5. Return the Result:

   • When the bottom-right corner is reached, return the cost.
   • If no valid path exists (though the problem guarantees one), return -1.

---

Complexity:

• Time Complexity: O(m x n), where m is the number of rows and n is the number of columns. Each cell is processed once.
• Space Complexity: O(m x n), for the visited array and deque.

This implementation works efficiently within the given constraints.

[topugit]

Thanks to solve the Minimum Obstacle Removal to Reach Corner problem

[mah-shamim]

Thanks