LeetCode-矩阵操作篇.md

LeetCode-矩阵操作篇

[toc]

LeetCode36

有效的数独

题干

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。 只需要根据以上规则，验证已经填入的数字是否有效即可。 空白格用 '.' 表示。

示例 1：

示例

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

解题思路

• 核心思路在用数组来记录是否当前的数字已经出现过
• 困难点在于如何判断3*3格子中是否出现过相同的数字，即找到(i,j)和对应的方格的映射关系
• 用(i/3) * 3 + j/3，其中(i/3) * 3，表示这个是第几行的3个格子，j/3表示这个是对应行的第几个格子
• 以(6,5)为例子，表示在第二行的第二个格子，即3+1(从0开始编号)。

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        int row[9][10] = {0}; //记录行信息
        int col[9][10] = {0}; //记录列信息
        int box[9][10] = {0}; //记录斜对角信息，当然也可以用3*3*9
        
        for (int i = 0; i < 9; i++){
            for (int j = 0; j < 9; j++){
                if (board[i][j] == '.') continue; //空格跳过
                int currNum = board[i][j] - '0';
                if(row[i][currNum]) return false; //i行信息判断是否已经出现相同数字
                if(col[j][currNum]) return false; //j列信息判断是否已经出现相同信息
                if(box[j/3+ (i/3)*3][currNum]) return false;
                //关键点在于此次，j/3+ (i/3)*3表示第几个9*9的子矩阵
                row[i][currNum] = 1;
                col[j][currNum] = 1;
                box[j/3+ (i/3)*3][currNum] = 1; //如果不曾出现，赋值对应位置，记录表明已经出现
            }
        }
        return true;
    }
};

LeetCode48

旋转图像

题干

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

示例

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

解题思路

• 找到旋转的规律，以2->6->8->4->2的角度来看，(i,j)的位置会旋转到(j, n- i-1)的位置
• 对应的4个数字各自重新复位，所以只需要遍历一半的数据即可。

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; i++){
            for (int j = 0; j < (n + 1)/ 2; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        } 
 		// 通过分析旋转的规律，可以知道(i,j)->(j, n-i-1)
        return;
    }
};

LeetCode 54

螺旋矩阵

题干

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

示例

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

解题思路

• 递归调用实现
• 主要注意判断 (1)同一行 (2) 同一列 (3) 唯一数等情况特殊处理
• (x1,y1)和(x2,y2)分别代表矩阵的左上角和右下角

class Solution {
public:
void helper(vector<vector<int>>& matrix, int x1, int y1, int x2, int y2, vector<int>& path){
        if (x1 > x2 || y1 > y2) return;

        if (x1 == x2 && y1 != y2){ //同一行的情况下的遍历
            for (int i = y1; i <= y2; i++){
            path.push_back(matrix[x1][i]);
            } 
        } 
        else if (x1 != x2 && y1 == y2){ //同一列的情况下遍历
            for (int i = x1; i <= x2; i++){
                path.push_back(matrix[i][y1]);
                }   
        } 
        else if (x1 == x2 && y1 == y2){ //唯一一个数的情况下的遍历
            path.push_back(matrix[x1][y1]);
        } else {
            for (int i = y1; i <= y2; i++){
                path.push_back(matrix[x1][i]);
            }
            for (int i = x1 + 1; i <= x2; i++){
                path.push_back(matrix[i][y2]);
            }
            for (int i = y2 - 1; i >= y1; i--){
                path.push_back(matrix[x2][i]);
            }
            for (int i = x2 - 1; i > x1; i--){
                path.push_back(matrix[i][y1]);
            }  //螺旋遍历，注意边界值
        }
        helper(matrix, x1 + 1,y1 + 1,x2 - 1, y2 - 1, path);//而后递归调用
        return;
    };
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int>path;
        helper(matrix,0,0,matrix.size() - 1, matrix[0].size() - 1,path);
        return path;
    }
};

LeetCode59

螺旋矩阵 II

题干

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

示例

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

class Solution {
public:
void helper(vector<vector<int>>& matrix, int x1, int y1, int x2, int y2, int& curr){
        if (x1 > x2 || y1 > y2) return;
        
        if (x1 == x2 && y1 == y2){
            matrix[x1][y1] = curr;
            return;
        } else {
            for (int i = y1; i <= y2; i++){
                matrix[x1][i] = curr;
                curr = curr + 1;
            }
            for (int i = x1 + 1; i <= x2; i++){
                matrix[i][y2] = curr;
                curr = curr + 1;
            }
            for (int i = y2 - 1; i >= y1; i--){
                matrix[x2][i] = curr;
                curr =curr + 1;
            }
            for (int i = x2 - 1; i > x1; i--){
                matrix[i][y1] = curr;
                curr = curr + 1;
            }
        }
        helper(matrix,x1+1,y1+1,x2-1,y2-1,curr);
        return;

    };
    vector<vector<int>> generateMatrix(int n) {
        vector<int> row(n,0);
        vector<vector<int>> ret(n, row);
        int curr = 1;
        helper(ret,0,0,n-1,n-1,curr);
        return ret;
    }
};

LeetCode73

矩阵置零

题干

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**

示例 1：

示例

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

解法

• 遍历矩阵，找到所有出现过0的行和列的下标值进行保存
• 而后对矩阵进行遍历，在保存的下标值出现过的行或者列进行置0操作

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        set<int> row;
        set<int> col;
        for (int i = 0; i < matrix.size(); i++){
            for (int j = 0; j < matrix[0].size(); j++){
                if (matrix[i][j] == 0){
                    row.insert(i);
                    col.insert(j);
                }
            } //找到所有出现过0的行和列
        }
        for (int i = 0; i < matrix.size(); i++){
            for (int j = 0; j < matrix[0].size(); j++){
                if (row.find(i) != row.end() || col.find(j) != col.end()){
                    matrix[i][j] = 0;
                }
            }
        } //对行和列进行置0操作
        return;
    }
};

LeetCode74

搜索二维矩阵

题干

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非递减顺序排列。 每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

示例

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

解题思路

• 解题思路主要在于从左下角开始遍历
• 如果当前数字比目标值大，则往上遍历
• 如果当前数字比目标值小，则往右遍历
• 下面题解是将整个矩阵拉成整个数组，而后进行二分查找即可。主要在于行列值的计算

class Solution {
public:

    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int row = matrix.size();
        int col = matrix[0].size();

        int start = 0;
        int end = matrix.size() * matrix[0].size() - 1;

        while(start <= end){
            int mid = start + (end - start) / 2;
            int i = mid / col;
            int j = mid % col;
            if (matrix[i][j] == target) return true;
            if (matrix[i][j] > target){
                end = mid - 1;
            } else {
                start = mid + 1; //二分查找，主要是行和列的变化
            }
        }
        return false;

    }
};

LeetCode130

被围绕的区域

题干

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

解题思路

• 这边利用的核心要点在于，只要与边界相接的'O'点就是无法被包围的
• 因此对于所有的边上的点进行深度优先遍历，将其进行标记
• 对于被标记过的点，即为和边界相同的'O'点，无法被包围
• 对于没有被标价的'O'点，即为被'X'包围的点，将其变为'X'

class Solution {
public:
    void dfs(vector<vector<char>>& board, int x, int y){
        if (x < 0 || y < 0 || x >= board.size() || y >= board[0].size() || board[x][y] != 'O'){
            return;
        }
        board[x][y] = 'A';
        dfs(board,x - 1, y);
        dfs(board,x + 1, y);
        dfs(board,x, y + 1);
        dfs(board,x, y - 1);
        return;

    }
    void solve(vector<vector<char>>& board) {
        int row = board.size();
        int col = board[0].size();

        for (int i = 0; i < col; i = i + 1){
                dfs(board,0,i);
                dfs(board,row - 1, i);
        }
        for (int i = 1; i < row - 1; i = i + 1){
            dfs(board,i, 0);
            dfs(board,i, col - 1);
        }
        for (int i = 0; i < row; i++){
            for (int j = 0; j < col;j++){
                if (board[i][j] == 'A'){
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O'){
                    board[i][j] = 'X';
                 }
            }
        }
        return;

    }
};

LeetCode200

岛屿数量

题干

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

解题思路

• 用深度优先遍历，如果是和边界相邻或者已经是标记过的或者是和水相邻，即为True
• 否则用'A'进行标记
• 遍历整个矩阵，如果是已经被标记过的，则不再进行遍历；每返回一次true即知新增一座岛屿

class Solution {
public:
    bool dfs(vector<vector<char>>& grid, int row, int col){
        if (row < 0 || col < 0 || row >= grid.size() || col >= grid[0].size() || grid[row][col] == '0' || grid[row][col] == 'A') return true;

        grid[row][col] = 'A'; //用字符标记已经遍历过

        return dfs(grid,row - 1,col) && dfs(grid,row + 1,col) && dfs(grid,row,col - 1) && dfs(grid,row,col + 1);
    }
    int numIslands(vector<vector<char>>& grid) {
        int ret = 0;
        for(int i = 0; i < grid.size(); i++){
            for (int j = 0; j < grid[0].size(); j++){
                if (grid[i][j] == 'A' || grid[i][j] == '0') continue;
                bool temp = dfs(grid, i, j);
                if (temp) ret = ret + 1;
                
            }
        }
        return ret;
    }
};

LeetCode240

搜索二维矩阵 II

题干

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。 每列的元素从上到下升序排列。

示例 1：

示例

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

解题思路

• 和上一题类似，从左下角开始遍历
• 如果比目标值小，则右移
• 比目标值大，则上移

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int row = matrix.size();
        int col = matrix[0].size();

        int s_x = row - 1;
        int s_y = 0;
        while(s_x >= 0 && s_y < col){
            if (matrix[s_x][s_y] == target) return true;
            if (matrix[s_x][s_y] < target) s_y += 1;
            else s_x -= 1;
        }
        return false;
        
    }
};

LeetCode289

生命游戏

题干

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡； 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活； 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡； 如果死细胞周围正好有三个活细胞，则该位置死细胞复活； 下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例

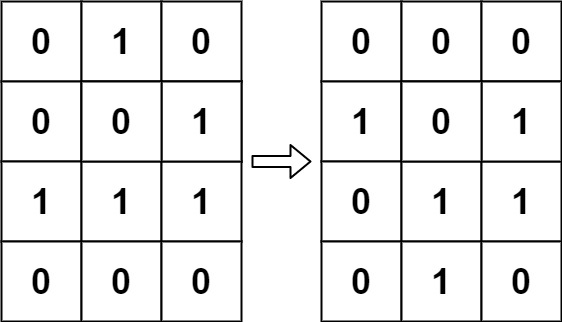
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

解题思路

• 主要的核心点在于，我们需要新定义： (1) 原来是死的，后来活了。(2) 原来是活的，后来死了。(3) 原来是活的，现在还是活的。(4) 原来是死的，现在还是死的。

class Solution {
public:
    void gameOfLife(vector<vector<int>>& board) {
        int neighbors[3] = {-1, 0, 1};
        int rows = board.size();
        int cols = board[0].size();

        for (int row = 0; row < rows; row++){
            for (int col = 0; col < cols; col++){
                int livenei = 0;
                for (int i = 0; i < 3; i++){
                    for (int j = 0; j < 3; j++){
                        if (!(neighbors[i] == 0 && neighbors[j] == 0)){
                            int r = row + neighbors[i];
                            int c = col + neighbors[j];

                            if (r >= 0 && c >= 0 && r < rows && c < cols && abs(board[r][c]) == 1){
                                livenei += 1;
                            }
                        }
                    }
                }

                if (board[row][col] == 1 && (livenei < 2 || livenei > 3)){
                    board[row][col] = -1;
                }
                if (board[row][col] == 0 && livenei == 3){
                    board[row][col] = 2;
                }
            }
        }
        for (int i = 0; i < rows; i++){
            for (int j = 0; j < cols; j++){
                if (board[i][j] > 0){
                    board[i][j] = 1;
                } else {
                    board[i][j] = 0;
                }
            }
        }
        return;

    }
};