Minitest1 (at the end):
-
The general search algorithm
- Problem-solving agents: find sequence of actions that achieve goals.
- Operators expand a state: generate new states from present ones.
- search strategy: tells which state to expand next.
- fringe or frontier: discovered states to be expanded
-
Some search strategies:
- Evaluation criteria:
- completeness: a search algorithm that is guaranteed to find a solution if there is one
- time efficiency:
- space efficiency:
- optimality of solution:
- Uninformed or blind searches:
- Breadth-first: (FIFO queuing strategy)
- complete: yes
- time and space: O(branch_factor^depth) (empirically space a larger problem than time)
- optimality: yes, if path cost non-decreasing with depth.
- Uniform Cost (BB) (expand lo cost fringe node)
- optimal: yes, if no negative costs
- a generalization of Breadth-first.
- Depth-first (uses a stack)
- completeness: no! may go down and not come back
- time: O(branch_factor^depth)
- space: O(depth)
- optimality: no! returns first found, not necessarily ideal
- depth-limited (DFS down to some cutoff)
- completeness: yes, provided solution exists before cutoff
- time: O(branch_factor^depth_limit)
- space: O(depth_limit)
- optimality: no!
- Iterative Deepening (successively increasing depth-limited)
- diameter of state space: max anticipated path length for most problems.
- completeness: yes (like Breadth-first)
- time: O(branch_factor^diameter)
- space: O(diameter) (like Depth-first)
- optimality: yes (like Breadth-first)
- Breadth-first: (FIFO queuing strategy)
- Informed searches:
- Best-first search (expand nodes according to some cost function)
- Greedy search (expand according to h(n)--cost to goal)
- completeness: no (could go down an endless branch)
- optimality: no (ignores cost from initial node)
- faster (on average) than uninformed algorithm
- A* search (combines uniform-cost search and greedy search)
- expand nodes according to the estimated total cost function, f(n) = g(n) + h(n)
- h(n) must always be optimistic (admissible)
- completeness: yes
- optimality: yes
- optimally efficient: no better algorithm with same knowledge
- Greedy search (expand according to h(n)--cost to goal)
- Heuristic functions
- Relax the demands of the problem
-
Admissible
- it never overestimates the cost of reaching the goal, i.e. the cost it estimates to reach the goal is not higher than the lowest possible cost from the current point in the path - optimistic nature.
-
Consistent
-
it estimates always less than or equal to the estimated distance from any neighboring vertex to the goal, plus the step cost of reaching that neighbor.
, N is any node in the graph and P is any descendant of N.
-
- Best-first search (expand nodes according to some cost function)
- Evaluation criteria:
Systems that describe a set of rules (productions) about behaviour. It represents a mechanism of goal finding through if-then rules or condition-action rules or situation-action rules or just productions. Eg: Knowledge Based Systems (KBS).
- Weak Methods
- Generic search techniques
- Subject to combinatorial explosion
- Informed Methods
- Have some sort of prior knowledge about the problem
- Forward Chaining - start from the data/premisses and move towards the objectives/conclusions.
- Good when the number of objectives is large
- eg: Symbolic Integration (moves from the integral form and finds the derivative, the opposite would not make sense)
- Backward Chaining - start from the objectives/conclusions and move towards the data/premisses
- Good when the number of objectives is small
- eg: Theorem prover (moves from the theorem and find the axioms, otherwise many theorems could be derived from a set of initial axioms)
Should be choosen individually for each problem.
- Graph
- Tree
The problem of efficiently representing a state or a state sequence. Many approaches exist and the answer varies from problem to problem:
- Record every state
- Record initial state and further changes from that
- Record the current state and the steps needed to go back to the previous states Faces the problem of representing things that change as a colateral effect. Eg: Turning a glass of water upside down has the colateral effect of spilling the water.
Used to represent the value of a given state in accordance to the desired goal.
Either can be transformed into the other by increasing (Graph -> Tree) or decreasing (Tree -> Graph) the number of nodes.
- Generate and Test
- Depth-first Search
- Breadth-first Search
- Backtracking
- Branch and Bound
- Hill Climbing
- Simulated Annealing
- Genetic Algorithms
- Decomposition
- Constraint Satisfaction
- Means-Ends Analysis
Genereates a potential solution (exhaustively) and tests it for a real solution.
 |
Transverses a Search Tree or Graph by exploring all the child nodes of the current node, and only backtracks when a leaf/node with no unexplored chil is found. |
 |
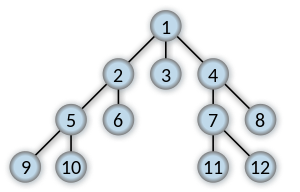Transverses a Search Tree or Graph by exploring all the nodes at a given level, before proceeding to their children at deeper levels |
 |
Search technique that proceeds the search untill a soution is proved to not be possible along that path, it then takes back steps, one a time, until it finds another node that does not impede a solution and delves into that path, repeating the process |
 |
Transverses a Search Tree by exploring branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm. |
 |
The hill-climbing search algorithm is simply a loop that continually moves in the direction of increasing value—that is, uphill. It terminates when it reaches a "peak" where no neighbor has a higher value. |
 |
Simulated Annealing combines hill climbing with a random walk in some way that yields
both efficiency and completeness.
It generates a random number and checks if it is below |
Comapre in terms of complexity and characteristics the search strategies of: depth first search (dfs), breadth first search (bfs), iterative deepening (id):
| Time complexity | Space complexity | Complete (guaranteed to find a solution) | Optimal (guaranteed to find the best solution) | |
|---|---|---|---|---|
| dfs | r^m | r * m (if it expands all sucessors before choosing the first), m otherwise | no | no |
| bfs | r^(p+1) (because it expands all the successors before navigating sideways) | same as time complexity (r^(p+1)) | yes | yes (if the utility is the length of the path) |
| id | r^p (because it does not expand the next successors) | same as dfs space complexity (r * m if...) | yes | yes (if the utility is the length of the path) |
Problem from figure 2.2 in Intelligent Systems for Engineering: A Knowledge-based Approach.
Question: Using A* on the field lots, what is the content of the openList and closedList right after node 4 is expanded? How is the next node choosen in A*?
Answer: openList = [2,5,6] and closedList = [1,3,4]. A* chooses the next node from openList that has the lowest f* value. Or the left one, if they have the same f* values.
Question: Given a tree of r = 2 (branching factor) and m = 2 (tree depth), with node values of 5,3,2,7, what are the values of α and β for each tree node and specify if all the tree nodes are visited.
Answer: node with value 7 is cut and the values of α and β can be visualized here.