errata

『ゼロから作る Deep Learning』の正誤表

下記の誤りがありました。お詫びして訂正いたします。

本ページに掲載されていない誤植など間違いを見つけた方は、japan＠oreilly.co.jpまでお知らせください。

第14刷まで

頁	誤	正
4章 P.188 L.6	なんだが不自然に	なんだか不自然に
5章 P.130 L.11	簡単に覚えることがでます。	簡単に覚えることができます。
6章 P.195 L.14	消去した割合	消去しなかった割合
6章 P.195 最終行	順伝搬	順伝播
6章 P.196 L.1	消去した割合	消去しなかった割合
6章 P.197 L.15	消去した割合	消去しなかった割合

第13刷まで

頁	誤	正
4章 P.88 L.13	2乗和誤差（mean squared error）でしょう。	2乗和誤差（sum of squared error）でしょう。
4章 P.89 L.5	def mean_squared_error(y, t):	def sum_squared_error(y, t):
4章 P.89 L.15	>>> mean_squared_error(np.array(y), np.array(t))	>>> sum_squared_error(np.array(y), np.array(t))
4章 P.89 L.20	>>> mean_squared_error(np.array(y), np.array(t))	>>> sum_squared_error(np.array(y), np.array(t))
4章 P.98 L.11,L.18	10e-50	1e-50
6章 P.176 L.4	4つの手法を説明してきましが、	4つの手法を説明してきましたが、
7章 P.227 L.16	def __init__(self, pool_h, pool_w, stride=1, pad=0):	def __init__(self, pool_h, pool_w, stride=2, pad=0):
8章 P.243 L.6	deep_conv_net_params.pkl	deep_convnet_params.pkl
索引 P.294	mean squared error ……… 88	sum of squared error ……… 88
索引 P.294	mean_squared_error() ……… 89	sum_squared_error() ……… 89

第12刷まで

頁	誤	正
1章 P.4 L.1	https://www.continuum.io/downloads	https://www.anaconda.com/distribution
5章 P.150 L.21	次ように	次のように

第11刷のみ

頁	誤	正
4章 P.112 L.2,L.4,L.5

第10刷まで

頁	誤	正
4章 P.94 l.12	return -np.sum(t * np.log(y)) / batch_size	return -np.sum(t * np.log(y + 1e-7)) / batch_size
4章 P.94 l.25	return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size	return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
4章 P.94 下	tがラベル表現の場合は、np.log( y[np.arange(batch_size), t] )として、同じ処理を実現します。	tがラベル表現の場合は、np.log( y[np.arange(batch_size), t] )として、同じ処理を実現します（ここでの説明は、見やすさを優先して「微小な値1e-7」の記載は省略します）。
4章 P.110 式4.8 補足
4章 P.111
5章 P.149 式5.14 補足
5章 P.156 l.15	この実装では、「3.5.2 ソフトマックス関数の実装上の注意」と「4.2.2 交差エントロピー誤差」で実装した関数	この実装では、「3.5.2 ソフトマックス関数の実装上の注意」と「4.2.4 ［バッチ対応版］交差エントロピー誤差の実装」で実装した関数

第8刷まで

頁	誤	正
全般 補足	行列の内積	行列の積
3章 P.56 l.19	行列Aの1次元目と行列Cの0次元目の次元数が一致していない、	行列Aの1次元目と行列Cの0次元目の次元の要素数が一致していない、
3章 P.73 l.25	そして、このMNSITデータセットは、	そして、このMNISTデータセットは、
4章 P.93 l.3	また、教師データは10次元のデータです。	また、教師データは10列のデータです。
4章 P.111 下	dWの中身を見ると、たとえば、$\mathbf{W}$の$w_{11}$はおよそ0.2ということが分かります。	dWの中身を見ると、たとえば、$\frac{\partial L}{\partial \mathbf{W}}$の$\frac{\partial L}{\partial \mathbf{w_{11}}}$はおよそ0.2ということが分かります。
6章 P.189 図6-17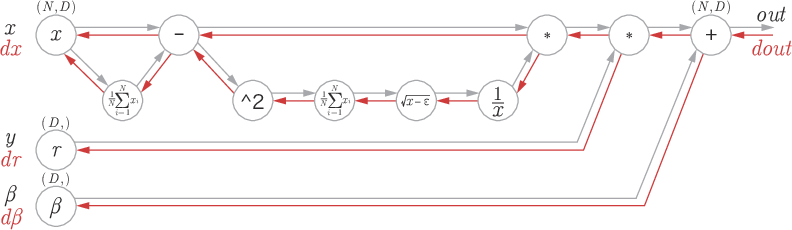
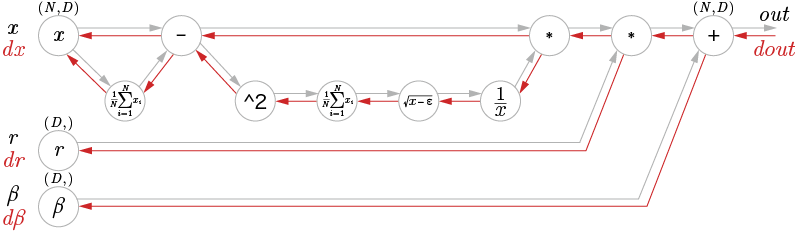7章 P.237 l.6	LeNetが今から20年以上も前に提案された	LeNetが今から20年近くも前に提案された
7章 P.237 l.9	LeNetが世に出てから20年以上が経過して、	LeNetが世に出てから20年近くが経過して、

第7刷まで

頁	誤	正
1章 P.17 図1-3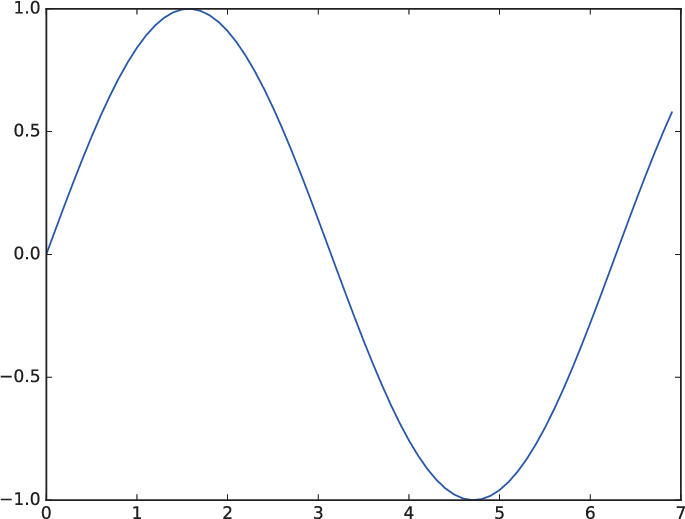
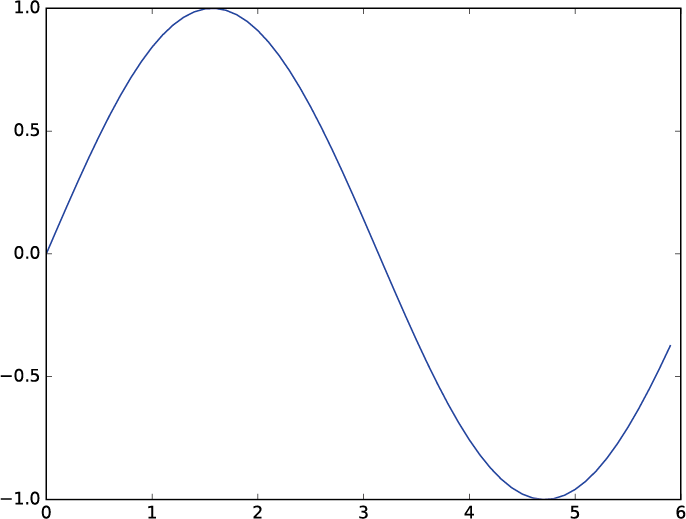2章 P34 L.13	第2層目の入力はyを出力する。	第2層目のニューロンはyを出力する。
4章 P.91 最終行	k次元目	k番目
4章 P.93 L.2	784次元	784列
4章 P.111 L.9	[[ 0.47355232, 0.9977393 , 0.84668094],	[[ 0.47355232 0.9977393 0.84668094]
4章 P.111 L.10	[ 0.85557411, 0.03563661, 0.69422093]])	[ 0.85557411 0.03563661 0.69422093]]
4章 P.111 L.15	[ 1.13282549 0.66052348 1.20919114]	[ 1.05414809 0.63071653 1.1328074]
5章 P.161 L.21	(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)	(x_train, t_train), (x_test, t_test) = \ 　　load_mnist(normalize=True, one_hot_label=True)
6章 P.200 L.8	「10 の階乗」	「10 のべき乗」
7章 P.232 L.6,7	self.layers['Affine2'] = Affine(self.params['W3'], 　　　　　　　　　　　　　　　self.params['b3'])	self.layers['Affine2'] = Affine(self.params['W3'], 　　　　　　　　　　　　　　　self.params['b3']) self.last_layer = SoftmaxWithLoss()

第5刷まで

頁	誤	正
2章 P.29 L.3	図2-5の真理値表を満たします。	図2-4の真理値表を満たします。
2章 P.33 L.19	XORは、図2-12に示すような多層構造のネットワークです。	XORは、図2-13に示すような多層構造のネットワークです。
3章 P.56 L.21	つまり、多次元配列の積では、2つの行列で対応する次元を一致させる必要があるということです。	つまり、多次元配列の積では、2つの行列で対応する次元の要素数を一致させる必要があるということです。
3章 P.78 L.25	上の結果から、対応する配列の次元数が一致していることを確認しましょう	上の結果から、多次元配列の対応する次元の要素数が一致していることを確認しましょう
3章 P.78 L.27	次元配列の対応する次元数が一致していますね。	次元配列の対応する次元の要素数が一致していますね。
3章 P.79 L.2	10次元の配列が出力されるという流れになっています。	1次元の配列（要素数10）が出力されるという流れになっています。
4章 P.106 L.8	どこに最小値を取る場所があるのか検討がつきません。	どこに最小値を取る場所があるのか見当がつきません。
4章 P.114 L.29	y = predict(x)	y = self.predict(x)
4章 P.118 L.4	(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)	(x_train, t_train), (x_test, t_test) = \ 　　load_mnist(normalize=True, one_hot_label=True)
4章 P.120 L.11	(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)	(x_train, t_train), (x_test, t_test) = \ 　　load_mnist(normalize=True, one_hot_label=True)
5章 P.147 L.20	対応する次元数を一致させるというのがポイントです。	対応する次元の要素数を一致させるというのがポイントです。
5章 P.147 L.21	対応する次元数を一致させる必要があります。	対応する次元の要素数を一致させる必要があります。
5章 P.147 図5-23のキャプション	図5-23 行列の内積では、対応させる次元数を一致させる	図5-23 行列の内積では、対応する次元の要素数を一致させる
5章 P.150 L.1	行列の内積では、対応する次元数を一致させる必要があり、	行列の内積では、対応する次元の要素数を一致させる必要があり、
5章 P.150 図5-26のキャプション	図5-26 行列の内積（「dot」ノード）の逆伝播は、行列の対応する次元数を一致させるように内積を	図5-26 行列の内積（「dot」ノード）の逆伝播は、行列の対応する次元の要素数を一致させるように内積を
6章 P.197 図6-23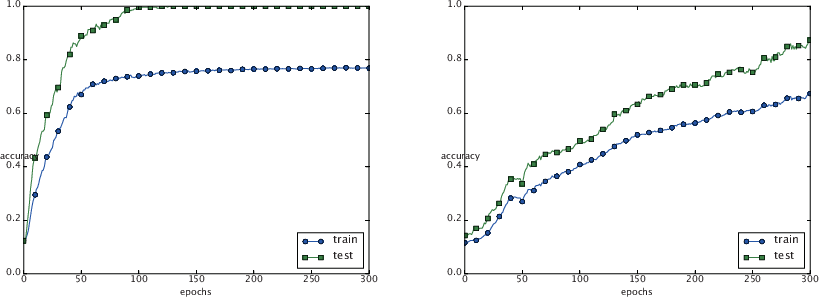

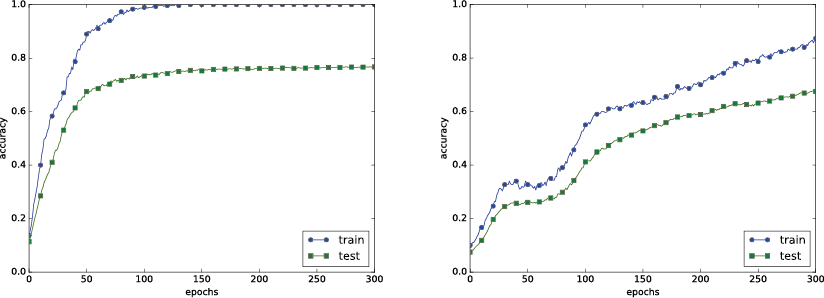第4刷まで

頁	誤	正
目次、5章、索引	連鎖率	連鎖律
4章 P.111 L.23	続いて、勾配を求めてみましょう。これまでどおり、numerical_gradient(f, x)を使って勾配を求めます。	続いて、勾配を求めてみましょう。これまでどおり、numerical_gradient(f, x)を使って勾配を求めます（ここで定義したf(W)という関数の引数Wは、ダミーとして設けたものです。これは、numerical_gradient(f, x)が内部でf(x)を実行するため、それと整合性がとれるようにf(W)を定義しました）。
7章 P.236 L.10,14	1989年	1998年

第3刷まで

頁	誤	正
3章 P.76 L.4	ch03/nueralnet_mnist.py	ch03/neuralnet_mnist.py
4章 P.89 L.19	>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.5, 0.0] >>> mean_squared_error(np.array(y), np.array(t)) 0.72250000000000003	>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] >>> mean_squared_error(np.array(y), np.array(t)) 0.59750000000000003
4章 P.91 L.15	>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.5, 0.0] >>> cross_entropy_error(np.array(y), np.array(t)) 2.3025850919940458	>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] >>> cross_entropy_error(np.array(y), np.array(t)) 2.3025840929945458
4章 P.117 L.29	ch04/train_nueralnet.py	ch04/train_neuralnet.py
4章 P.118 L.7	# ハイパーパラメータ iters_num = 10000 batch_size = 100 learning_rate = 0.1	# ハイパーパラメータ iters_num = 10000 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1
5章 P.127 L.23	各ノードでは単純な計算をに集中することで、	各ノードでは単純な計算に集中することで、
5章 P.162 L.19	ch05/train_nueralnet.py	ch05/train_neuralnet.py

第2刷まで

頁	誤	正
2章 P.24 L.1	両方が1のときだけ0を出力し、それ以外は0を出力します。	両方が1のときだけ0を出力し、それ以外は1を出力します。

第1刷

頁	誤	正
7章 P.227 図7-20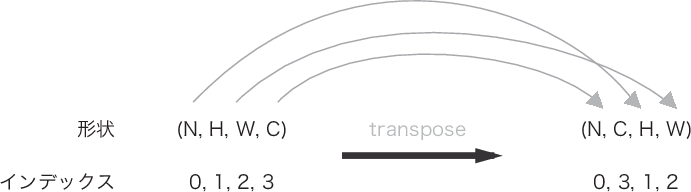
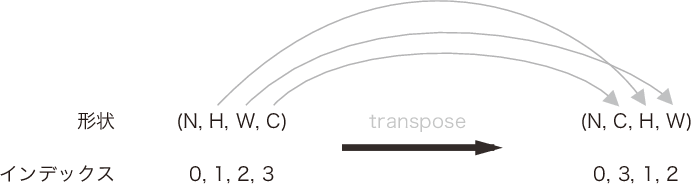