shortestPathInABinaryMatrix.md

Problem

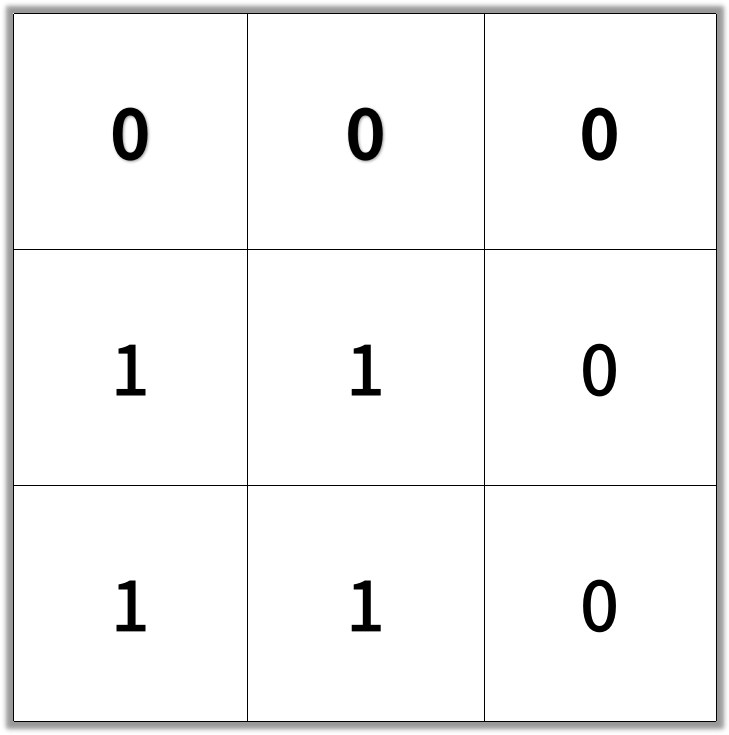
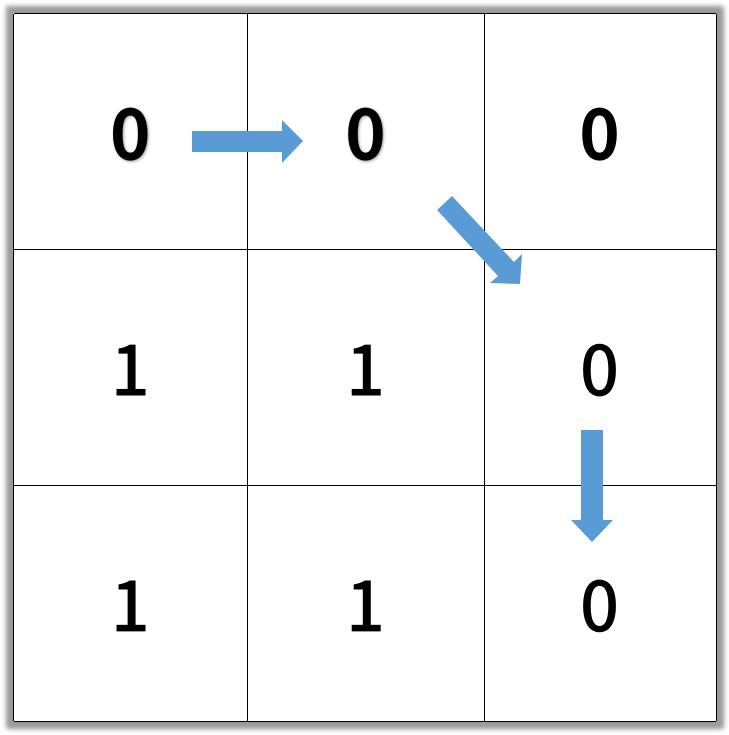
In an N by N square grid, each cell is either empty (0) or blocked (1).
Return the length of the shortest such clear path from top-left to bottom-right.
If such a path does not exist, return -1.

Examples

Solution

Time - O(N*N) Space-O(N*N)

package main
type node struct{
    x,y,dist int
}

func shortestPathBinaryMatrix(grid [][]int) int {
    n := len(grid) // matrix is square so rows and cols are same
    if grid[0][0]==1 || grid[n-1][n-1]==1{
        //if first or last grid is blocked then not possible
        return -1
    }
    queue := make([]node,0)
    queue = append(queue,node{x:0,y:0,dist:1})
    yarr := []int{1,1,0,-1,-1,-1,0,1}
    xarr := []int{0,1,1,1,0,-1,-1,-1}
    
    for len(queue)>0{
        front:=queue[0]
        queue = queue[1:]
        if front.x==n-1 && front.y==n-1{
            return front.dist
        }
        for k:=0;k<len(xarr);k++{
            i,j := xarr[k]+front.x, yarr[k]+front.y
            if isSafe(i,j,n) && grid[i][j]==0{
                queue=append(queue,node{x:i,y:j,dist:front.dist+1})
                //mark them visited
                grid[i][j]=1
            }
        }
    }
    return -1
}

func isSafe(i,j,n int) bool{
    if i<0 || i>=n || j<0 || j>=n{
        return false
    }
    return true
}