-
Notifications
You must be signed in to change notification settings - Fork 290
/
Copy pathactivation.md
130 lines (50 loc) · 5.03 KB
/
activation.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
## LeakyReLU层 {#leakyrelu}
---
LeakyRelU是修正线性单元(Rectified Linear Unit,ReLU)的特殊版本,当不激活时,LeakyReLU仍然会有非零输出值,从而获得一个小梯度,避免ReLU可能出现的神经元“死亡”现象。即,`f(x)=alpha * x for x <0 f(x) = x for x>=0`
## PReLU层 {#prelu}
---
该层为参数化的ReLU(Parametric ReLU),表达式是:`f(x) = alpha * x for x <0`,`f(x) = x for x>=0`,此处的`alpha`
为一个与xshape相同的可学习的参数向量。
## ELU层 {#elu}
---
ELU层是指数线性单元(Exponential Linera Unit),表达式为: 该层为参数化的ReLU(Parametric ReLU),表达式是:
`f(x) = alpha * (exp(x) - 1.) for x < 0`,`f(x) = x for x>=0`
## ThresholdedReLU层 {#thresholdedrelu}
---
该层是带有门限的ReLU,表达式是:`f(x) = x for x >theta`,`f(x) = 0 otherwise`
激活函数的作用:
1,激活函数是用来加入非线性因素,解决模型所不能解决的问题。
2,激活函数可以用来组合训练数据的特征,特征的充分组合。
下面我分别对激活函数的两个作用进行解释。
1
加入非线性因素,解决非线性问题
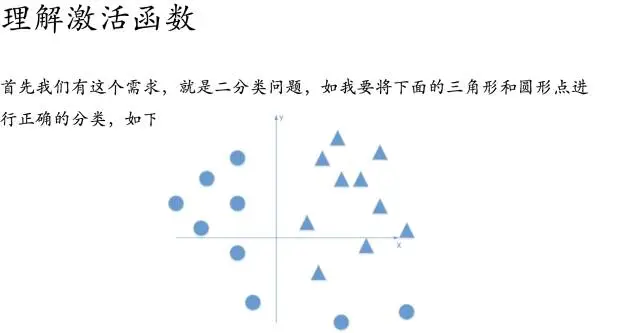

好吧,很容易能够看出,我给出的样本点根本不是线性可分的,一个感知器无论得到的直线怎么动,都不可能完全正确的将三角形与圆形区分出来,那么我们很容易想到用多个感知器来进行组合,以便获得更大的分类问题,好的,下面我们上图,看是否可行

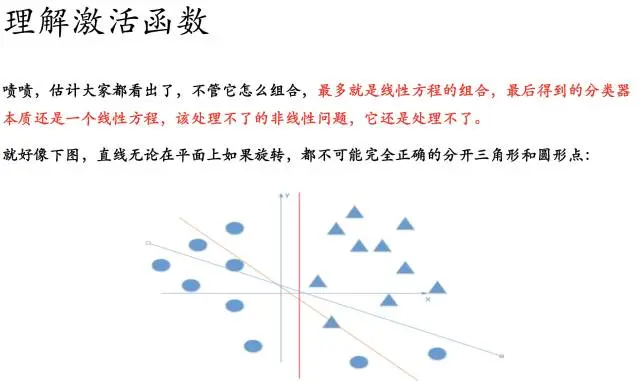
好的,我们已经得到了多感知器分类器了,那么它的分类能力是否强大到能将非线性数据点正确分类开呢~我们来分析一下:

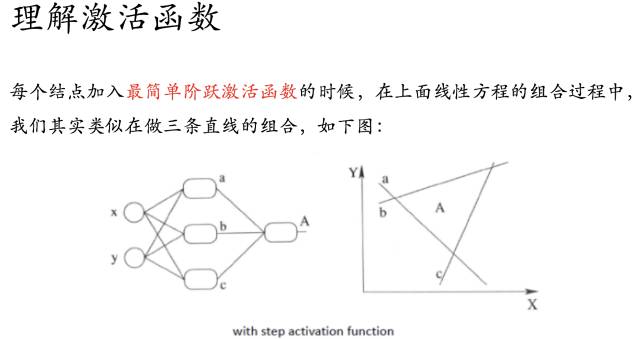
如果我们的每一个结点加入了阶跃函数作为激活函数的话,就是上图描述的
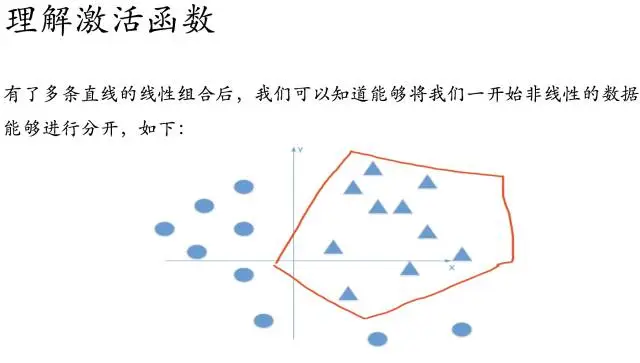
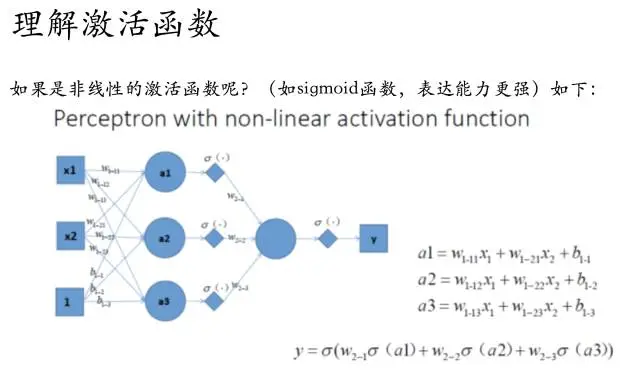
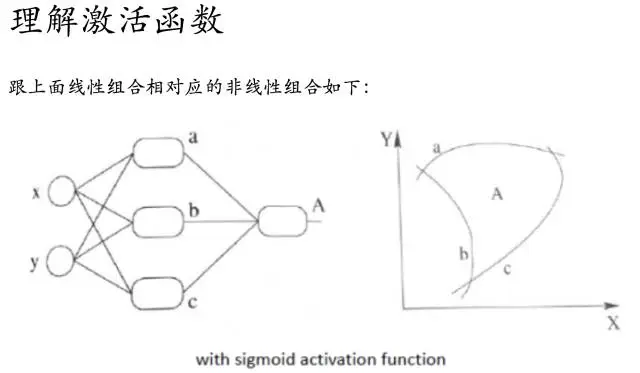

那么随着不断训练优化,我们也就能够解决非线性的问题了~
所以到这里为止,我们就解释了这个观点,加入激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题。
_下面我来讲解另一个作用_
2
激活函数可以用来组合训练数据的特征,特征的充分组合

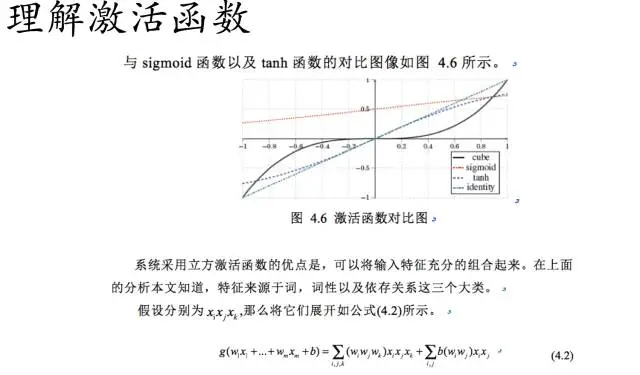
我们可以通过上图可以看出,立方激活函数已经将输入的特征进行相互组合了。


通过泰勒展开,我们可以看到,我们已经构造出立方激活函数的形式了。
于是我们可以总结如下:
3
总结

这就把原来需要领域知识的专家对特征进行组合的情况,在激活函数运算后,其实也能够起到特征组合的作用。(只要激活函数中有能够泰勒展开的函数,就可能起到特征组合的作用)
这也许能给我们一些思考。