-
Notifications
You must be signed in to change notification settings - Fork 290
/
Copy pathbptt.md
80 lines (40 loc) · 3.32 KB
/
bptt.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
随时间反向传播(BPTT)算法
---
先简单回顾一下RNN的基本公式:
$$s_t = \tanh (Ux_t+Ws_{t-1})$$
$$\hat y_t=softmax(Vs_t)$$
RNN的损失函数定义为交叉熵损失:
$$E_t(y_t,\hat y_t)=-y_t\log\hat y_t $$
$$E(y,\hat y)=\sum_{t}E_t(y_t, \hat y_t)=-\sum_{t}y_t\log\hat y_t$$
$$y_t$$是时刻t的样本实际值, $$\hat y\_t$$是预测值,我们通常把整个序列作为一个训练样本,所以总的误差就是每一步的误差的加和。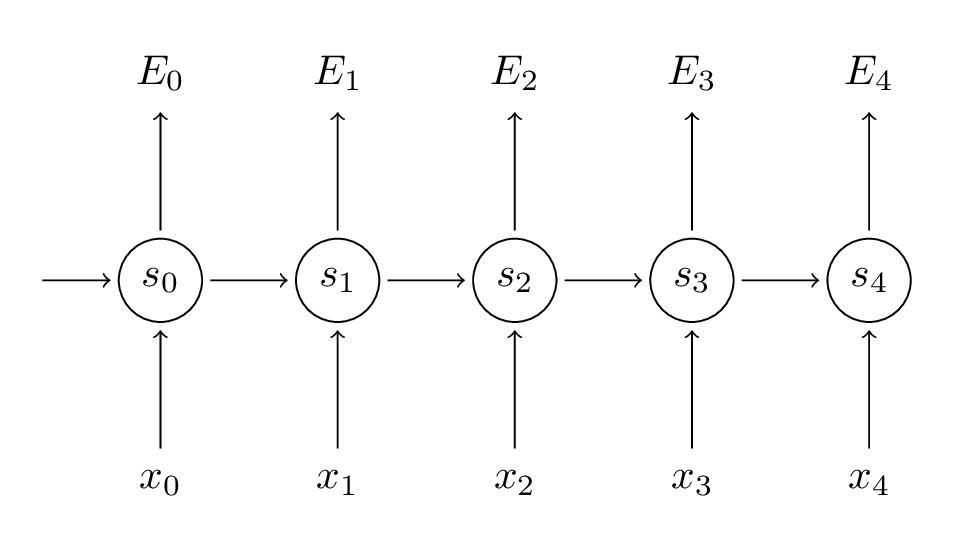我们的目标是计算损失函数的梯度,然后通过梯度下降方法学习出所有的参数U, V, W。比如:$$\frac{\partial E}{\partial W}=\sum_{t}\frac{\partial E_t}{\partial W}$$
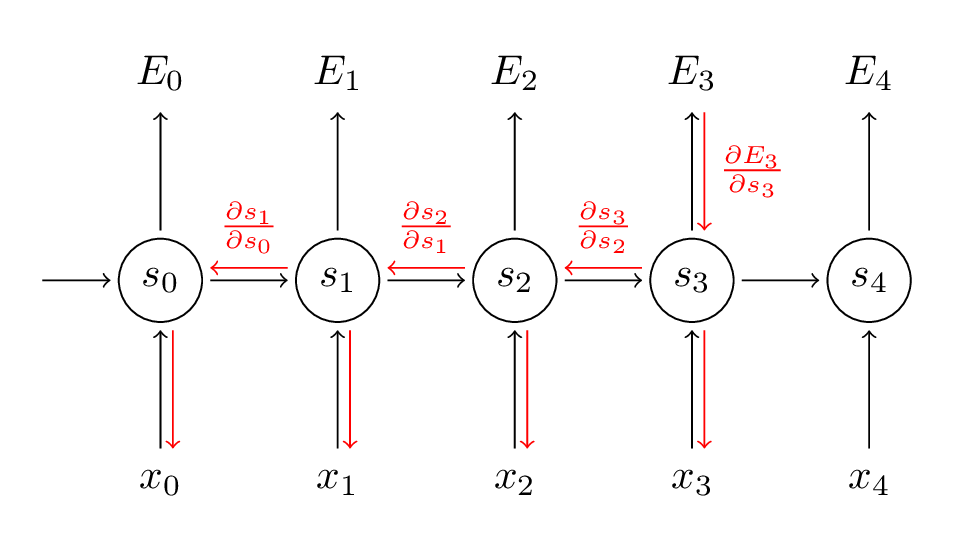为了更好理解BPTT我们来推导一下公式:
前向 前向传播1:
$$a_0 = x_0 * u$$
$$b_0 = s_{-1} * w$$
$$z_0 = a_0 + b_0 + k$$
$$s_0 = func(z_0)$$ \($$func$$ 是 sig或者tanh\)
前向 前向传播2:
$$a_1 = x_1 * u$$
$$b_1 = s_0 * w$$
$$z_1 = a_1 + b_1+k$$
$$s_1 = func(z_1)$$\($$func$$ 是 sig 或者tanh\)
$$q = s_1 * v_1$$
$$z_t = u*x_t + w*s_{t-1} + k$$
$$s_t = func(z_t)$$
输出 层:
$$o = func(q)$$\($$func$$ 是 softmax\)
$$E = func(o)$$\($$func$$ 是 x-entropy\)
下面 是U的推导
$$\partial E/\partial u = \partial E/\partial u_1 + \partial E/\partial u_0$$
$$\partial E/\partial u_1 = \partial E/\partial o * \partial o/\partial q * \partial q/\partial s_1 * \partial s_1/\partial z_1 * \partial z_1/\partial a_1 * \partial a_1/\partial u_1$$
$$\partial E/\partial u_0 = \partial E/\partial o * \partial o/\partial q * \partial q/\partial s_1 * \partial s_1/\partial z_1 * \partial z_1/\partial b_1 * \partial b_1/\partial s_0 * \partial s_0/dz_0 * \partial z_0/\partial a_0 * \partial a_0/\partial u_0$$
$$\partial E/\partial u = \partial E/\partial o * \partial o/\partial q * v_1 * \partial s_1/\partial z_1 * ((1 * x_1) + (1 * w_1 * \partial s_0/\partial z_0 * 1 * x_0))$$
$$\partial E/\partial u = \partial E/\partial o * \partial o/\partial q * v_1 * \partial s_1/\partial z_1 * (x_1 + w_1 * \partial s_0/\partial z_0 * x_0)$$
W参数的推导如下
$$\partial E/\partial w = \partial E/\partial o * \partial o/\partial q * v_1 * \partial s_1/\partial z_1 * (s_0 + w_1 * \partial s_0/\partial z_0 * s_{-1})$$
总结
$$\dfrac{\partial{L}}{\partial{u}}=\sum_t \dfrac{\partial{L}}{\partial{u_t}} = \dfrac{\partial L}{\partial o} \dfrac{\partial o}{\partial s_1} \dfrac{\partial s_1}{\partial u_1}+\dfrac{\partial L}{\partial o} \dfrac{\partial o}{\partial s_1}\dfrac{\partial s_1}{\partial s_0}\dfrac{\partial s_0}{\partial u_0}$$
$$\dfrac{\partial{L}}{\partial{w}}=\sum_t \dfrac{\partial{L}}{\partial{w_t}} = \dfrac{\partial L}{\partial o} \dfrac{\partial o}{\partial s_1} \dfrac{\partial s_1}{\partial w_1}+\dfrac{\partial L}{\partial o} \dfrac{\partial o}{\partial s_1}\dfrac{\partial s_1}{\partial s_0}\dfrac{\partial s_0}{\partial w_0}$$
$$x_t$$是时间t的输入
[](https://i.stack.imgur.com/B15TJm.png)
更多了解RNN,推荐[Goodfellow et al RNN chapter](http://www.deeplearningbook.org/contents/rnn.html)和Andrej Karpathy [minimal character RNN](https://gist.github.com/karpathy/d4dee566867f8291f086)实现。