-
Notifications
You must be signed in to change notification settings - Fork 290
/
Copy pathspectral.md
194 lines (99 loc) · 16.8 KB
/
spectral.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
# 谱聚类(spectral clustering)原理
---
谱聚类(spectral clustering)是广泛使用的聚类算法,比起传统的K-Means算法,谱聚类对数据分布的适应性更强,聚类效果也很优秀,同时聚类的计算量也小很多,更加难能可贵的是实现起来也不复杂。在处理实际的聚类问题时,个人认为谱聚类是应该首先考虑的几种算法之一。下面我们就对谱聚类的算法原理做一个总结。
# 1. 谱聚类概述
谱聚类是从图论中演化出来的算法,后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
乍一看,这个算法原理的确简单,但是要完全理解这个算法的话,需要对图论中的无向图,线性代数和矩阵分析都有一定的了解。下面我们就从这些需要的基础知识开始,一步步学习谱聚类。
# 2. 谱聚类基础之一:无向权重图
由于谱聚类是基于图论的,因此我们首先温习下图的概念。对于一个图G,我们一般用点的集合V和边的集合E来描述。即为G\(V,E\)。其中V即为我们数据集里面所有的点$$(v_1, v_2,...v_n)$$。对于V中的任意两个点,可以有边连接,也可以没有边连接。我们定义权重$$w_{ij}$$为点$$v_i$$和点$$v_j$$之间的权重。由于我们是无向图,所以$$w_{ij} = w_{ji}$$。
对于有边连接的两个点$$v_i$$和$$v_j$$,$$w_{ij} >0$$,对于没有边连接的两个点$$v_i$$和$$v_j$$,$$w_{ij} = 0$$。对于图中的任意一个点$$v_i$$,它的度$$d_i$$定义为和它相连的所有边的权重之和,即$$d_i = \sum\limits_{j=1}^{n}w_{ij}$$
利用每个点度的定义,我们可以得到一个nxn的度矩阵D,它是一个对角矩阵,只有主对角线有值,对应第i行的第i个点的度数,定义如下:
$$\mathbf{D} = \left( \begin{array}{ccc} d_1& \ldots & \ldots \\ \ldots &d_2 & \ldots \\ \vdots & \vdots & \ddots \\ \ldots & \ldots & d_n \end{array} \right)$$
利用所有点之间的权重值,我们可以得到图的邻接矩阵W,它也是一个nxn的矩阵,第i行的第j个值对应我们的权重$$w_{ij}$$。
除此之外,对于点集V的的一个子集$$A \subset V$$,我们定义:
|A|: = 子集A中点的个数
$$
vol(A): = \sum\limits_{i \in A}d_i
$$
# 3. 谱聚类基础之二:相似矩阵
在上一节我们讲到了邻接矩阵W,它是由任意两点之间的权重值$$w_{ij}$$组成的矩阵。通常我们可以自己输入权重,但是在谱聚类中,我们只有数据点的定义,并没有直接给出这个邻接矩阵,那么怎么得到这个邻接矩阵呢?
基本思想是,距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,不过这仅仅是定性,我们需要定量的权重值。一般来说,我们可以通过样本点距离度量的相似矩阵S来获得邻接矩阵W。
构建邻接矩阵W的方法有三类。$$\epsilon$$-邻近法,K邻近法和全连接法。
对于$$\epsilon$$-邻近法,它设置了一个距离阈值$$\epsilon$$,然后用欧式距离$$s_{ij}$$度量任意两点$$x_i$$和$$x_j$$的距离。即相似矩阵的$$s_{ij} = ||x_i-x_j||_2^2$$, 然后根据$$s_{ij}$$和$$\epsilon$$的大小关系,来定义邻接矩阵W如下:
$$W_{ij}= \begin{cases} 0& {s_{ij} > \epsilon}\\ \epsilon& {s_{ij}\leq \epsilon} \end{cases}$$
从上式可见,两点间的权重要不就是$$\epsilon$$,要不就是0,没有其他的信息了。距离远近度量很不精确,因此在实际应用中,我们很少使用$$\epsilon$$-邻近法。
第二种定义邻接矩阵W的方法是K邻近法,利用KNN算法遍历所有的样本点,取每个样本最近的k个点作为近邻,只有和样本距离最近的k个点之间的$$w_{ij}$$ > 0。但是这种方法会造成重构之后的邻接矩阵W非对称,我们后面的算法需要对称邻接矩阵。为了解决这种问题,一般采取下面两种方法之一:
第一种K邻近法是只要一个点在另一个点的K近邻中,则保留$$S_{ij}$$
$$W_{ij}=W_{ji}= \begin{cases} 0& {x_i \notin KNN(x_j) \;and \;x_j \notin KNN(x_i)}\\ exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in KNN(x_j)\; or\; x_j \in KNN(x_i}) \end{cases}$$
第二种K邻近法是必须两个点互为K近邻中,才能保留$$S_{ij}$$
$$W_{ij}=W_{ji}= \begin{cases} 0& {x_i \notin KNN(x_j) \;or\;x_j \notin KNN(x_i)}\\ exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in KNN(x_j)\; and \; x_j \in KNN(x_i}) \end{cases}$$
第三种定义邻接矩阵W的方法是全连接法,相比前两种方法,第三种方法所有的点之间的权重值都大于0,因此称之为全连接法。可以选择不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF,此时相似矩阵和邻接矩阵相同:$$W_{ij}=S_{ij}=exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})$$
在实际的应用中,使用第三种全连接法来建立邻接矩阵是最普遍的,而在全连接法中使用高斯径向核RBF是最普遍的。
# 4. 谱聚类基础之三:拉普拉斯矩阵
单独把拉普拉斯矩阵\(Graph Laplacians\)拿出来介绍是因为后面的算法和这个矩阵的性质息息相关。它的定义很简单,拉普拉斯矩阵L= D-W。D即为我们第二节讲的度矩阵,它是一个对角矩阵。而W即为我们第二节讲的邻接矩阵,它可以由我们第三节的方法构建出。
拉普拉斯矩阵有一些很好的性质如下:
1)拉普拉斯矩阵是对称矩阵,这可以由D和W都是对称矩阵而得。
2)由于拉普拉斯矩阵是对称矩阵,则它的所有的特征值都是实数。
3)对于任意的向量f,我们有$$f^TLf = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2$$
这个利用拉普拉斯矩阵的定义很容易得到如下:
$$f^TLf = f^TDf - f^TWf = \sum\limits_{i=1}^{n}d_if_i^2 - \sum\limits_{i,j=1}^{n}w_{ij}f_if_j=\frac{1}{2}(\sum\limits_{i=1}^{n}d_if_i^2 - 2\sum\limits_{i,j=1}^{n}w_{ij}f_if_j + \sum\limits_{j=1}^{n}d_jf_j^2) = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2$$
4\) 拉普拉斯矩阵是半正定的,且对应的n个实数特征值都大于等于0,即$$0 =\lambda_1 \leq \lambda_2 \leq...\leq \lambda_n$$, 且最小的特征值为0,这个由性质3很容易得出。
# 5. 谱聚类基础之四:无向图切图
对于无向图G的切图,我们的目标是将图G(V,E)切成相互没有连接的k个子图,每个子图点的集合为:$$A_1,A_2,..A_k$$,它们满足$$A_i \cap A_j = \emptyset$$,且$$A_1 \cup A_2 \cup ... \cup A_k = V$$.
对于任意两个子图点的集合$$A, B \subset V,A \cap B = \emptyset$$, 我们定义A和B之间的切图权重为:$$W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij}$$
那么对于我们k个子图点的集合:$$A_1,A_2,..A_k$$,我们定义切图cut为:$$cut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits\_{i=1}^{k}W(A\_i, \overline{A}\_i)$$
其中$$\overline{A}_i$$为$$A_i$$的补集,意为除$$A_i$$子集外其他V的子集的并集。
那么如何切图可以让子图内的点权重和高,子图间的点权重和低呢?一个自然的想法就是最小化cut(A_1,A_2,...A_k), 但是可以发现,这种极小化的切图存在问题,如下图:
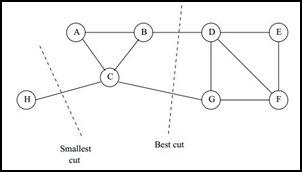
我们选择一个权重最小的边缘的点,比如C和H之间进行cut,这样可以最小化cut\(A\_1,A\_2,...A\_k\), 但是却不是最优的切图,如何避免这种切图,并且找到类似图中"Best Cut"这样的最优切图呢?我们下一节就来看看谱聚类使用的切图方法。
# 6. 谱聚类之切图聚类
为了避免最小切图导致的切图效果不佳,我们需要对每个子图的规模做出限定,一般来说,有两种切图方式,第一种是RatioCut,第二种是Ncut。下面我们分别加以介绍。
## 6.1 RatioCut切图
RatioCut切图为了避免第五节的最小切图,对每个切图,不光考虑最小化$$cut(A_1,A_2,...A_k)$$,它还同时考虑最大化每个子图点的个数,即:$$RatioCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i)}{|A_i|}$$
那么怎么最小化这个RatioCut函数呢?牛人们发现,RatioCut函数可以通过如下方式表示。
我们引入指示向量$$h_j =\{h_1, h_2,..h_k\}\; j =1,2,...k$$,对于任意一个向量$$h_j$$, 它是一个n维向量(n为样本数),我们定义$$h_{ji}$$为:
$$h_{ji}= \begin{cases} 0& {v_i \notin A_j}\\ \frac{1}{\sqrt{|A_j|}}& {v_i \in A_j} \end{cases}$$
那么我们对于$$h_i^TLh_i$$,有:
$$\begin{aligned} h_i^TLh_i & =\frac{1}{2}\sum\limits_{m=1}^{k}\sum\limits_{n=1}^{k}w_{mn}(h_{im}-h_{in})^2 \\& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{|A_i|}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{|A_i|}} )^2\\& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{|A_i|} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{|A_i|}\\& = \frac{1}{2}(cut(A_i, \overline{A}_i) \frac{1}{|A_i|} + cut(\overline{A}_i, A_i) \frac{1}{|A_i|}) \\& = \frac{cut(A_i, \overline{A}_i)}{|A_i|} \\& = RatioCut(A_i, \overline{A}_i) \end{aligned}$$
上述第(1)式用了上面第四节的拉普拉斯矩阵的性质3. 第二式用到了指示向量的定义。可以看出,对于某一个子图i,它的RatioCut对应于$$h_i^TLh_i$$,那么我们的k个子图呢?对应的RatioCut函数表达式为:$$RatioCut(A_1,A_2,...A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = tr(H^TLH)$$
其中$$tr(H^TLH)$$为矩阵的迹。也就是说,我们的RatioCut切图,实际上就是最小化我们的$$tr(H^TLH)$$。注意到$$H^TH=I$$,则我们的切图优化目标为:$$arg\;min(H)\; tr(H^TLH) \;\; s.t.\;H^TH=I$$
注意到我们H矩阵里面的每一个指示向量都是n维的,向量中每个变量的取值为0或者$$\frac{1}{\sqrt{|A_j|}}$$,就有$$2^n$$种取值,有k个子图的话就有k个指示向量,共有$$k2^n$$种H,因此找到满足上面优化目标的H是一个NP难的问题。那么是不是就没有办法了呢?
注意观察$$tr(H^TLH)$$中每一个优化子目标$$h_i^TLh_i$$,其中h是单位正交基, L为对称矩阵,此时$$h_i^TLh_i$$的最大值为L的最大特征值,最小值是L的最小特征值。如果你对主成分分析PCA很熟悉的话,这里很好理解。在PCA中,我们的目标是找到协方差矩阵(对应此处的拉普拉斯矩阵L)的最大的特征值,而在我们的谱聚类中,我们的目标是找到目标的最小的特征值,得到对应的特征向量,此时对应二分切图效果最佳。也就是说,我们这里要用到维度规约的思想来近似去解决这个NP难的问题。
对于h\_i^TLh\_i,我们的目标是找到最小的L的特征值,而对于tr\(H^TLH\) = \sum\limits\_{i=1}^{k}h\_i^TLh\_i,则我们的目标就是找到k个最小的特征值,一般来说,k远远小于n,也就是说,此时我们进行了维度规约,将维度从n降到了k,从而近似可以解决这个NP难的问题。
通过找到L的最小的k个特征值,可以得到对应的k个特征向量,这k个特征向量组成一个nxk维度的矩阵,即为我们的H。一般需要对H里的每一个特征向量做标准化,即$$h_i = h_i / |h_i|$$.
由于我们在使用维度规约的时候损失了少量信息,导致得到的优化后的指示向量h对应的H现在不能完全指示各样本的归属,因此一般在得到nxk维度的矩阵H后还需要对每一行进行一次传统的聚类,比如使用K-Means聚类.
## 6.2 Ncut切图
Ncut切图和RatioCut切图很类似,但是把Ratiocut的分母$$|Ai|$$换成$$vol(A_i)$$. 由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说Ncut切图优于RatioCut切图。$$NCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i)}{vol(A_i)}$$
对应的,Ncut切图对指示向量h做了改进。注意到RatioCut切图的指示向量使用的是$$\frac{1}{\sqrt{|A_j|}}$$标示样本归属,而Ncut切图使用了子图权重$$\frac{1}{\sqrt{vol(A_j)}}$$来标示指示向量h,定义如下:
$$h_{ji}= \begin{cases} 0& {v_i \notin A_j}\\ \frac{1}{\sqrt{vol(A_j)}}& {v_i \in A_j} \end{cases}$$
那么我们对于$$h_i^TLh_i$$,有:
$$\begin{aligned} h_i^TLh_i & =\frac{1}{2}\sum\limits_{m=1}^{k}\sum\limits_{n=1}^{k}w_{mn}(h_{im}-h_{in})^2 \\& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{vol(A_j)}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{vol(A_j)}} )^2\\& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{vol(A_j)} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{vol(A_j)}\\& = \frac{1}{2}(cut(A_i, \overline{A}_i) \frac{1}{vol(A_j)} + cut(\overline{A}_i, A_i) \frac{1}{vol(A_j)}) \\& = \frac{cut(A_i, \overline{A}_i)}{vol(A_j)} \\& = NCut(A_i, \overline{A}_i) \end{aligned}$$
推导方式和RatioCut完全一致。也就是说,我们的优化目标仍然是$$NCut(A_1,A_2,...A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = tr(H^TLH)$$
但是此时我们的$$H^TH \neq I$$,而是$$H^TDH = I$$。推导如下:$$h_i^TDh_i = \sum\limits_{j=1}^{n}h_{ij}^2d_j =\frac{1}{vol(A_i)}\sum\limits_{v_j \in A_i}w_{v_j} = \frac{1}{vol(A_i)}vol(A_i) =1$$
也就是说,此时我们的优化目标最终为:$$arg\;min(H)\; tr(H^TLH) \;\; s.t.\;H^TDH=I$$
此时我们的H中的指示向量h并不是标准正交基,所以在RatioCut里面的降维思想不能直接用。怎么办呢?其实只需要将指示向量矩阵H做一个小小的转化即可。
我们令$$H = D^{-1/2}F$$, 则:$$H^TLH = F^TD^{-1/2}LD^{-1/2}F,H^TDH=F^TF = I$$,也就是说优化目标变成了:$$arg\;min(F)\; tr(F^TD^{-1/2}LD^{-1/2}F) \;\; s.t.\;F^TF=I$$
可以发现这个式子和RatioCut基本一致,只是中间的L变成了$$D^{-1/2}LD^{-1/2}$$。这样我们就可以继续按照RatioCut的思想,求出$$D^{-1/2}LD^{-1/2}$$的最小的前k个特征值,然后求出对应的特征向量,并标准化,得到最后的特征矩阵F,最后对F进行一次传统的聚类(比如K-Means)即可。
一般来说,$$D^{-1/2}LD^{-1/2}$$相当于对拉普拉斯矩阵L做了一次标准化,即$$\frac{L_{ij}}{\sqrt{vol(A_i)vol(A_j)}}$$
# 7. 谱聚类算法流程
铺垫了这么久,终于可以总结下谱聚类的基本流程了。一般来说,谱聚类主要的注意点为相似矩阵的生成方式(参见第二节),切图的方式(参见第六节)以及最后的聚类方法(参见第六节)。
最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式,最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。
输入:样本集$$D=(x_1,x_2,...,x_n)$$,相似矩阵的生成方式, 降维后的维度$$k_1$$, 聚类方法,聚类后的维度$$k_2$$
输出: 簇划分$$C(c_1,c_2,...c_{k_2})$$.
1\) 根据输入的相似矩阵的生成方式构建样本的相似矩阵S
2)根据相似矩阵S构建邻接矩阵W,构建度矩阵D
3)计算出拉普拉斯矩阵L
4)构建标准化后的拉普拉斯矩阵$$D^{-1/2}LD^{-1/2}$$
5)计算$$D^{-1/2}LD^{-1/2}$$最小的$$k_1$$个特征值所各自对应的特征向量f
6\) 将特征向量f标准化,最终组成$$n \times k_1$$维的特征矩阵F
7)对F中的每一行作为一个$$k_1$$维的样本,共n个样本,用输入的聚类方法进行聚类,聚类维数为$$k_2$$。
8)得到簇划分$$C(c_1,c_2,...c_{k_2})$$.
# 8. 谱聚类算法总结
谱聚类算法是一个使用起来简单,但是讲清楚却不是那么容易的算法,它需要你有一定的数学基础。如果你掌握了谱聚类,相信你会对矩阵分析,图论有更深入的理解。同时对降维里的主成分分析也会加深理解。
下面总结下谱聚类算法的优缺点。
谱聚类算法的主要优点有:
1)谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2)由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有:
1)如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
2\) 聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。