Pagerank.md

layout	title	order	permalink
page	Pagerank	5	/pagerank/

1. Consider any $$2\times 2$$ matrix A and apply the matrix on a $$2\times1$$ vector $$v$$. Keep applying this matrix and notice that the direction converges, while the magnitude may get larger. Keep normalizing $$v$$ and notice the direction to which it converges. Use Numpy

2. Consider the previous $$2\times 2$$ matrix and find out its eigenvalue and eigenvectors. What do you observe?

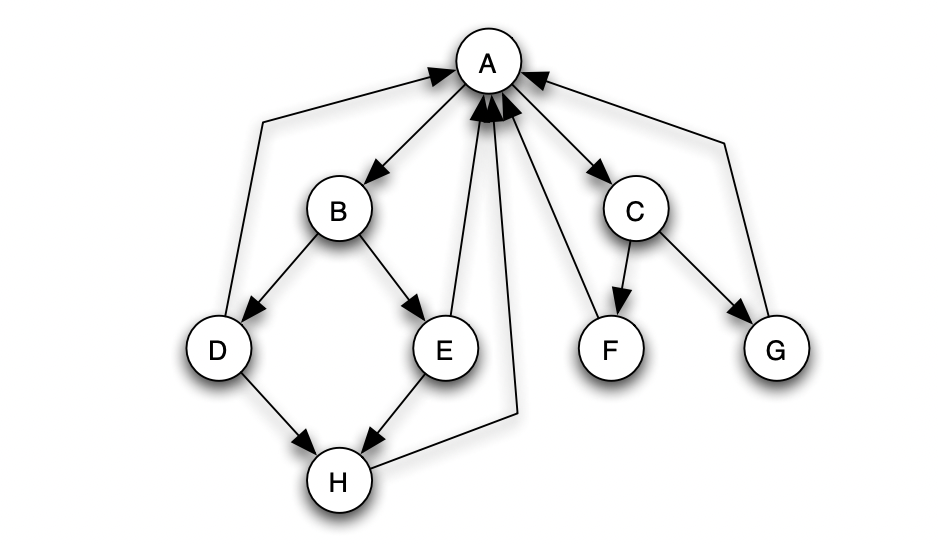
3. Consider the following network: Assign values to the nodes so that the value of the nodes = sum of the values of the nodes from which there are incoming edges. For example the value of F should be half of the value of C. The value of E should be half the value of B and so on.

4. Write down the edge list of the above graph and use networkx to run a random walk on it. What is the distribution of visits?

5. Are the following two questions equivalent?:

   • If I were to give pocket money to two of my daughters: 500 rupees each.

   • I toss a coin and give my elder daughter 1000 rupees if its heads or the younger daughter 1000 rupees if its tails.

     Are these two statements equivalent? In the sense that, by the end of the year, do you think both my daughters would have received, more or less, the same amount of money?

6. Consider the adjacency matrix of the above graph, tweak it and observe that the principal eigen vector is same as the answer to the previous question. (Principal Eigen Vector is defined as the eigen vector corresponding to the highest eigen value)

7. Can you consider a network of vertices, in the order of thousands and figure out the answer? You will observe that the best method to use is the random walk (with teleportation). why?