diff --git a/404.html b/404.html new file mode 100644 index 0000000..086a5c9 --- /dev/null +++ b/404.html @@ -0,0 +1,25 @@ +--- +permalink: /404.html +layout: default +--- + + + +
+

404

+ +

Page not found :(

+

The requested page could not be found.

+
diff --git a/Faq.md b/Faq.md new file mode 100644 index 0000000..3282421 --- /dev/null +++ b/Faq.md @@ -0,0 +1,11 @@ +--- +layout: page +title: FAQ +permalink: /faq/ +order: 2 +--- + + +**Where do I start from? ** + +This page will soon be updated. diff --git a/Galaxy.md b/Galaxy.md new file mode 100644 index 0000000..1dcd3c6 --- /dev/null +++ b/Galaxy.md @@ -0,0 +1,14 @@ +--- +layout: page +title: Galaxy +order: 5 +permalink: /galaxy/ +--- + +* TOC +{:toc} + +Coming soon. + + + diff --git a/Gemfile b/Gemfile new file mode 100644 index 0000000..fbde605 --- /dev/null +++ b/Gemfile @@ -0,0 +1,4 @@ + +source "https://rubygems.org" +gem "minima" +gem "webrick", "~> 1.8" diff --git a/Gemfile 2 b/Gemfile 2 new file mode 100644 index 0000000..fbde605 --- /dev/null +++ b/Gemfile 2 @@ -0,0 +1,4 @@ + +source "https://rubygems.org" +gem "minima" +gem "webrick", "~> 1.8" diff --git a/Gemfile 2.lock b/Gemfile 2.lock new file mode 100644 index 0000000..4b9b8f5 --- /dev/null +++ b/Gemfile 2.lock @@ -0,0 +1,79 @@ +GEM + remote: https://rubygems.org/ + specs: + addressable (2.8.5) + public_suffix (>= 2.0.2, < 6.0) + colorator (1.1.0) + concurrent-ruby (1.2.2) + em-websocket (0.5.3) + eventmachine (>= 0.12.9) + http_parser.rb (~> 0) + eventmachine (1.2.7) + ffi (1.16.3) + forwardable-extended (2.6.0) + google-protobuf (3.24.4-arm64-darwin) + http_parser.rb (0.8.0) + i18n (1.14.1) + concurrent-ruby (~> 1.0) + jekyll (4.3.2) + addressable (~> 2.4) + colorator (~> 1.0) + em-websocket (~> 0.5) + i18n (~> 1.0) + jekyll-sass-converter (>= 2.0, < 4.0) + jekyll-watch (~> 2.0) + kramdown (~> 2.3, >= 2.3.1) + kramdown-parser-gfm (~> 1.0) + liquid (~> 4.0) + mercenary (>= 0.3.6, < 0.5) + pathutil (~> 0.9) + rouge (>= 3.0, < 5.0) + safe_yaml (~> 1.0) + terminal-table (>= 1.8, < 4.0) + webrick (~> 1.7) + jekyll-feed (0.17.0) + jekyll (>= 3.7, < 5.0) + jekyll-sass-converter (3.0.0) + sass-embedded (~> 1.54) + jekyll-seo-tag (2.8.0) + jekyll (>= 3.8, < 5.0) + jekyll-watch (2.2.1) + listen (~> 3.0) + kramdown (2.4.0) + rexml + kramdown-parser-gfm (1.1.0) + kramdown (~> 2.0) + liquid (4.0.4) + listen (3.8.0) + rb-fsevent (~> 0.10, >= 0.10.3) + rb-inotify (~> 0.9, >= 0.9.10) + mercenary (0.4.0) + minima (2.5.1) + jekyll (>= 3.5, < 5.0) + jekyll-feed (~> 0.9) + jekyll-seo-tag (~> 2.1) + pathutil (0.16.2) + forwardable-extended (~> 2.6) + public_suffix (5.0.3) + rb-fsevent (0.11.2) + rb-inotify (0.10.1) + ffi (~> 1.0) + rexml (3.2.6) + rouge (4.1.3) + safe_yaml (1.0.5) + sass-embedded (1.69.3-arm64-darwin) + google-protobuf (~> 3.23) + terminal-table (3.0.2) + unicode-display_width (>= 1.1.1, < 3) + unicode-display_width (2.5.0) + webrick (1.8.1) + +PLATFORMS + arm64-darwin-22 + +DEPENDENCIES + minima + webrick (~> 1.8) + +BUNDLED WITH + 2.4.18 diff --git a/Gemfile.lock b/Gemfile.lock new file mode 100644 index 0000000..4b9b8f5 --- /dev/null +++ b/Gemfile.lock @@ -0,0 +1,79 @@ +GEM + remote: https://rubygems.org/ + specs: + addressable (2.8.5) + public_suffix (>= 2.0.2, < 6.0) + colorator (1.1.0) + concurrent-ruby (1.2.2) + em-websocket (0.5.3) + eventmachine (>= 0.12.9) + http_parser.rb (~> 0) + eventmachine (1.2.7) + ffi (1.16.3) + forwardable-extended (2.6.0) + google-protobuf (3.24.4-arm64-darwin) + http_parser.rb (0.8.0) + i18n (1.14.1) + concurrent-ruby (~> 1.0) + jekyll (4.3.2) + addressable (~> 2.4) + colorator (~> 1.0) + em-websocket (~> 0.5) + i18n (~> 1.0) + jekyll-sass-converter (>= 2.0, < 4.0) + jekyll-watch (~> 2.0) + kramdown (~> 2.3, >= 2.3.1) + kramdown-parser-gfm (~> 1.0) + liquid (~> 4.0) + mercenary (>= 0.3.6, < 0.5) + pathutil (~> 0.9) + rouge (>= 3.0, < 5.0) + safe_yaml (~> 1.0) + terminal-table (>= 1.8, < 4.0) + webrick (~> 1.7) + jekyll-feed (0.17.0) + jekyll (>= 3.7, < 5.0) + jekyll-sass-converter (3.0.0) + sass-embedded (~> 1.54) + jekyll-seo-tag (2.8.0) + jekyll (>= 3.8, < 5.0) + jekyll-watch (2.2.1) + listen (~> 3.0) + kramdown (2.4.0) + rexml + kramdown-parser-gfm (1.1.0) + kramdown (~> 2.0) + liquid (4.0.4) + listen (3.8.0) + rb-fsevent (~> 0.10, >= 0.10.3) + rb-inotify (~> 0.9, >= 0.9.10) + mercenary (0.4.0) + minima (2.5.1) + jekyll (>= 3.5, < 5.0) + jekyll-feed (~> 0.9) + jekyll-seo-tag (~> 2.1) + pathutil (0.16.2) + forwardable-extended (~> 2.6) + public_suffix (5.0.3) + rb-fsevent (0.11.2) + rb-inotify (0.10.1) + ffi (~> 1.0) + rexml (3.2.6) + rouge (4.1.3) + safe_yaml (1.0.5) + sass-embedded (1.69.3-arm64-darwin) + google-protobuf (~> 3.23) + terminal-table (3.0.2) + unicode-display_width (>= 1.1.1, < 3) + unicode-display_width (2.5.0) + webrick (1.8.1) + +PLATFORMS + arm64-darwin-22 + +DEPENDENCIES + minima + webrick (~> 1.8) + +BUNDLED WITH + 2.4.18 diff --git a/Handbook.md b/Handbook.md new file mode 100644 index 0000000..5f52985 --- /dev/null +++ b/Handbook.md @@ -0,0 +1,66 @@ +--- +layout: page +title: Handbook +permalink: /handbook/ +toc: true +--- + +* TOC +{:toc} + +# Introduction + +This is a first course in mathematics with emphasis on helping a learner with a bunch of tools and techniques required for studying several aspects of data sciences. We will illustrate the ideas through questions and puzzles. We would like to replace theorems with intuition and give pointers to inspired students to look up material for further study. By the end of the course, the student will be confident on the basics of linear algebra and probability. The course will end with a couple of exemplary ideas in data sciences and the importance of the math thus studied. + + +# Expectations from the course +An important aspect of any course that is heavy on math, is to develop confidence to read up abstract material. The symbolc manipulation and logical reasoning are toolkits to infer unambiguously. It helps to stay confident and continuously interact with peers/TAs/Professor. Expect the material to be hard on your minds to begin with, but one will surely feel comfortable with time. An important tip is to take a relook at a mathematical concept multiple times, asking what is the question for which the concept is an answer. It helps to solve questions that challenge your conceptual understanding than solve multiple problems of similar type. + + +# Grading +## Performance Points + +There will be performance points assigned to every student using the following rule: + +| | | +| ---------------------------------------------------- | ----------------: | +| Attendance in classes/labs | 2 per hour | +| Late for the class/lab (irrespective of the urgency) | -10 per class/lab | +| Plagiarism/Cheating/Misconduct | PP will drop to 0 | +| Challenge Assignment | X | + +* If a student misses a lab or class, his/her $$PP$$ will be uniformly distributed to the rest of the class who were present. For example in a class of 30, if 10 people are absent for a lab session, 40 $$PP$$ will be distributed to the remaining 20 students. Each student will get $$\frac{40}{20}=2$$. +* A student coming late for the class, loses 10 $PP$ and this will be uniformly distributed to all those present in the class. +* X denotes that it is discretionary. The instructor can provide challenge assignments from time to time which will add in extra _PP_ s to your credit. +* Plagiarism/Cheating/Misconduct will result in the reset of the performance points. It will roll back to 0. The only way we will figure out plagiarism is through viva voce. +* The deficit $$ PP $$s will be assigned by the instructor based on his discretion, evaluated based on sincerity and overall conduct. +* This will be in practice starting from September 1st 2022. + + + +## Evaluation and Grades + +Final grades will be calculated based on the following rule: +$$\left(\frac{PP}{100}.Total\right)+\left( \frac{PP}{8}\right)$$ + +Where _PP_ stands for _Performance Points_ and _Total_ is the marks secured from theory, lab and project components. + +**Evaluation** + +| Type | |Marks| +|--|--|--| +|Theory Internals|Involves theory related grading: quiz and written assignments|10| +|Theory Externals|Final Theory Exam|35| +|Lab Internals|Grading based on lab performance and viva voce|10| +|Lab Externals|Final Lab Exam|35| +|Final Project||10| + + +## Theory Assignments +Theory assignments will involve writeups that are mostly straight forward and will be indicative of the difficulty in the mid term and final exams. Questions for the final exam will be consequential concepts from the assignments. It would help if assignments are taken seriously for the student to secure good marks in the exams. + +## Lab Assignments +Lab assignments will involve you to work on programming based questions. These can be take home tests or in lab tests. The difficulty level is indicative of the final lab exam questions. The evaluation of lab assignments will involve a strong viva voce component. + +## Project +The student will be asked to pick a project from a list of topics. The projects will mostly be explorative in nature. Every project will be executed by a team of at most 2 people. Evaluation of the project will be based on the report and presentation. diff --git a/Introduction.md b/Introduction.md new file mode 100644 index 0000000..2b4998f --- /dev/null +++ b/Introduction.md @@ -0,0 +1,7 @@ +--- +layout: page +title: Introduction +permalink: /codershigh/introduction/ +--- + +We will soon be composing an introduction for this initiaitve. $$a^2$$ $b^45$ \ No newline at end of file diff --git a/LICENSE.txt b/LICENSE.txt new file mode 100644 index 0000000..0e7ecd8 --- /dev/null +++ b/LICENSE.txt @@ -0,0 +1,21 @@ +The MIT License (MIT) + +Copyright (c) 2016-present Parker Moore and the minima contributors + +Permission is hereby granted, free of charge, to any person obtaining a copy +of this software and associated documentation files (the "Software"), to deal +in the Software without restriction, including without limitation the rights +to use, copy, modify, merge, publish, distribute, sublicense, and/or sell +copies of the Software, and to permit persons to whom the Software is +furnished to do so, subject to the following conditions: + +The above copyright notice and this permission notice shall be included in +all copies or substantial portions of the Software. + +THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR +IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, +FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE +AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER +LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, +OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN +THE SOFTWARE. diff --git "a/Leastsquares 9.53.52\342\200\257AM.md" "b/Leastsquares 9.53.52\342\200\257AM.md" new file mode 100644 index 0000000..a88f343 --- /dev/null +++ "b/Leastsquares 9.53.52\342\200\257AM.md" @@ -0,0 +1,52 @@ +--- +layout: page +title: Let us Understand the Least Understood, Fair and Square! +order: 5 +permalink: /leastsquares/ +--- + +1. We encounter equations very often in our lives. Consider for example, the following situation at ___Baker's Cafe___. The manager has a very important estimate to make. Mostly, visitors at his cafe happen to be families and they are often comprised of Children and/or Adults. He observes that there are 3 adults and 1 child at a table and their bill turns out to be Rs.1200/-. There is yet another table with 2 children and 1 adult and their bill comes out to be Rs.1000/-. Can the manager estimate the consumption of a Child/Adult? This is popularly called the _Simultaneous Equations_ and we all remember from our school days, multiple ways in which these can be solved.
+$$ 3A + 1C = 1200 $$ +$$ 1A + 2C = 1000 $$ + +2. While we were taught the so called two variables and two unknowns, what if there were more equations than unknowns?
+$$ 3A + 1C = 1200 $$ +$$ 1A + 2C = 1000 $$ +$$ 1A + 1C = 900 $$ + + +3. Note that the previous question can be modelled as a matrix: + + $$ 3A + 1C = 1200 $$ + $$ 1A + 2C = 1000 $$ + $$ 1A + 1C = 900 $$ + + Observe this is same as : + + $$ \left( \begin{matrix} 3 & 1 \\1 & 2 \\1 & 1 \\\end{matrix}\right) $$ + $$\left( + \begin{matrix} + B\\ + C\\ + \end{matrix} + \right)$$ + = + $$ + \left( + \begin{matrix} + 1200\\ + 1000\\ + 900\\ + \end{matrix} + \right) + $$ + +4. The best way to solve is, is to guess the values :-). Can you write a python code to guess the values? + +5. How do you solve this mathematically? There are two nice ways of solving this: + - Model this as a question of inverting a rectangular matrix and find the solution. (Whoa! my teacher never taught me that!) + - Model this as a funtion of two variables and solve it using partial differentiation (Eeks!) + + + + diff --git a/Linalg75 2.md b/Linalg75 2.md new file mode 100644 index 0000000..5365a02 --- /dev/null +++ b/Linalg75 2.md @@ -0,0 +1,453 @@ +--- +layout: page +title: Oceanverse +order: 5 +permalink: /linalg75/ +--- + +* TOC +{:toc} + + +# Linear Algebra + +1. Consider the matrix + $$ + \left[ \begin{array}{cc} + 1 & 2\\ 3 & 4 + \end{array}\right] + $$ + - What does it remind you of? + - What does it denote? + - Where and why do we use a matrix? + - Can you enlist a few applications of matrices? +
+ +2. Define a function. What is a surjective, injective and bijective + function? + +3. Given an example of a function + $$ + f:\mathbb{R}^2\rightarrow\mathbb{R}^2 + $$ + +4. Given an example of a very nice function + $$f:\mathbb{R}^2\rightarrow\mathbb{R}^2$$ + - Make extra efforts to make this function really nice. + - Explain what is so nice about your + function? + - Why should one study such functions? +
+5. Define a function + $$ \phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2 $$, which satisfies the following property: The point $$ \phi(2,3)=(7,4) $$. Note that this function should be defined at all points on $$\mathbb{R}^2$$. + - What are the properties of your function? Observe it + microscopically. +
+ +6. Given a function $$\phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2$$ + which satisfies the following two conditions: + + $$\phi(u+v)=\phi(u) +\phi(v)$$ + + $$\phi(\alpha v)=\alpha\phi(v)$$ + + * What can one say of such functions? + * Observe this function closely, such functions form the crux of several discplines, mainly of sciences and engineering. Spend at least 20 minutes dissecting them to the best possible extent. +
+7. Consider $$\mathbb{R}^2$$ what are all the properties of this set? + $$\mathbb{R}^2$$ is called a space of all vectors, aka a vector space. + Lookup for the definition of a vector space. + +8. A subset of a vector space which in itself is a vector space is + caled a subspace. Given an example of a subspace of $$\mathbb{R}^2$$. + +9. Given a vector $$(1,7)$$ what does the set + $$\{ \alpha(1,7) | \alpha \in \mathbb{R}\}$$ represent? Is it a + subspace of $$\mathbb{R}^2$$? + +10. Is $$\mathbb{R}^3$$ a vector space? + +11. Conside the two points $$(1,2,3)$$ and $$(4,5,7)\in \mathbb{R}^3$$. What + does the following set denote: + $$\{\alpha(1,2,3)+\beta(4,5,7) | \alpha, \beta \in \mathbb{R}\}$$. + Is this a subspace? + +12. Consider a straight line $$y=2x+1$$ in $$\mathbb{R}^2$$, does it form a + subspace of $$\mathbb{R}^2$$? + +13. Consider a unit circle in $$\mathbb{R}^2$$, centered at origin, is it + a subspace of $$\mathbb{R}^2$$? + +14. What are all the subspaces of $$\mathbb{R}^2$$? + +15. What are all the subspaces of $$\mathbb{R}^3$$? + +16. Given $$\mathbb{R}^3$$, pick any two points $$u,v\in \mathbb{R}^3$$. + Note that $$\{\alpha u+\beta v | \alpha, \beta \in \mathbb{R}\}$$ is a + subspace of $$\mathbb{R}^3$$. Generalize this idea! + +17. The set $$\{\alpha u + \beta v | \alpha, \beta \in \mathbb{R}\}$$ is + called the linear combination of vectors $$u$$ and $$v$$. We can + generalize this to $$k$$ vectors. Observe what this set is all about? + +18. We say that a vector $$w$$ is manufactured by $$u$$ and $$v$$ if + $$w\in \{\alpha u +\beta v | \alpha, \beta \in \mathbb{R} \}$$. + +19. Show that $$(1,2,3)$$ and $$(4,5,6)$$ can manufacture $$(7,8,9)$$. Also + $$(4,5,6)$$ and $$(7,8,9)$$ can manufacture $$(1,2,3)$$. Finally $$(4,5,6)$$ + can be manufactured by the other two vectors. + +20. Can $$(2,1,0)$$ and $$(3,0,8)$$ manufacture $$(1,1,1)$$ ? + +21. Can $$(0,0,1)$$ and $$(0,1,0)$$ manufacture $$(1,0,0)$$? + +22. When can two vectors in $$\mathbb{R}^3$$ manufacture a given third + vector? + +23. When can two vectors in $$\mathbb{R}^3$$ fail to manufacture a given + third vector? + +24. If $$\{u,v,w\}$$ are such that a vector in this set can be + manufactured by some vectors in the same set, then such a set is + called a linearly dependent set. + +25. Give examples of a linearly dependent set in $$\mathbb{R}^3$$ and get + conversant with the definition. + +26. If $$\{u,v,w\}$$ are such that no vector in this set can be + manufactured by any combination of vectors in the same set, then such + a set is called a linearly independent set. + +27. Give examples of a linearly dependent set in $$\mathbb{R}^3$$ and + $$\mathbb{R}^2$$ and get conversant with the definition. + +28. Are $$(1,2), (3,4)$$ linearly independent in $$\mathbb{R}^2$$? Prove! + +29. Are $$(1,1),(2,3),(7,17)$$ Linearly Independent or Dependent? + +30. - Construct a set of 3 vectors that are Linearly Independent in + $$\mathbb{R}^2$$. Can you? + + - Construct a set of 3 vectors that are Linearly Independent in + $$\mathbb{R}^3$$. Can you? + + - Construct a set of $$k$$ vectors that are Linearly Independent in + $$\mathbb{R}^k$$. Can you? + + - Construct a set of $$k+1$$ vectors that are Linearly Independent in + $$\mathbb{R}^k$$. Can you? + +31. - Show that in $$\mathbb{R}^2$$ we can at most have 2 Linearly + Independent vectors. + + - Show that in $$\mathbb{R}^3$$ we can at most have 3 Linearly + Independent vectors. + + - Show that in $$\mathbb{R}^n$$ we can at most have $$n$$ Linearly + Independent vectors. + +32. Set of any two linearly independent vectors in $$\mathbb{R}^2$$ is + called a basis. Set of any three linearly independent vectors in + $$\mathbb{R}^3$$ is called a basis. Similarly, for $$n$$. + +33. Show that a basis can manufacture any vector of the vector + space. + +34. Show that any set of linearly independent vectors form a subset of + some basis. In other words, one can include a few more elements to a + linearly independent set and make it a basis. + +35. Show that the number of elements in any basis for a given vector + space is always constant. + +36. Try taking a few vectors in $$\mathbb{R}^3$$ and discuss its linear + independence or linear dependence. Try atleast 10 examples and + familiarize yourself. + +37. Show that any 3 vectors on a plane passing through the origin in + $$\mathbb{R}^3$$ cannot be linearly independent. Prove. + +38. What are all the subspaces of $$R^3$$. + +39. Consider a subspace of $$R^3$$ and write down its basis. Do this for 3 + to 4 different subspaces. + +40. Give an example of a function + $$f:\mathbb{R}^2 \rightarrow \mathbb{R}^2$$ such that the range of the + function is the straight line $$y=10x$$. + +41. As an example consider the following basis set of + $$\mathbb{R}^2 : \left \{(1,2),(2,2)\right \}$$. Construct a function + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ such that: + + $$\phi(u+v)=\phi(u)+\phi(v)$$ + + $$\phi(\alpha u)= \alpha \phi(u)$$ + + Such a function is called a LT function, + + - Where is (1,2) and (2,2) mapped? + + - Where is (1,0) and (0,1) mapped? + + - What is the range of this function? + +42. Consider a function $$\phi$$ which is LT which maps + + $$\phi(1,2)=(3,4)$$ + + $$\phi(6,6)= (2,0)$$ + + - How many such functions can you construct? + + - What is the range of this function? + +43. Discuss the range of the following functions, given their values at + a few points: + + $$\phi(1,2)=(3,4)$$ $$\&$$ $$\phi(1,1)=(6,8)$$ + + $$\phi(1,1)=(2,2)$$ $$\&$$ $$\phi(3,3)=(4,4)$$ + + $$\phi(1,2)=(3,5)$$ $$\&$$ $$\phi(0,8)=(3,0)$$ + + $$\phi(-2,2)=(0,0)$$ $$\&$$ $$\phi(8,2)=(1,1)$$ + + $$\phi(1,1)=(2,2)$$ $$\&$$ $$\phi(1,2)=(3,3)$$ + +44. Give an example of an LT function which maps a L.I. set of vectors + to a L.I. set of vectors i.e. + $$\phi:\mathbb{R}^2 \rightarrow \mathbb{R}^2$$, where + $$\left \{ u,v \right \}$$ are L.I. $$\&$$ + $$\left \{\phi(u), \phi(v)\right \}$$ are also L.I. + +45. Same as the previous question, but $$\left \{ u,v \right \}$$ is L.I. + and $$\left \{\phi(u), \phi(v)\right \}$$ is L.D.\ + What can one say about the range? + +46. Note that range of a L.I function is always a subspace. + +47. Note that the set N=$$\{v: \phi(v)=0\}$$ is a subspace of $$R^2$$ where + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ is L.I . Take atleast 5 + different examples of L.I functions and see if this is true. The set + $$N\subseteq Domain$$ is called the null space of $$\phi$$. + +48. Construct a Linear Transformation + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$, + $$\phi(0,1)=(3,4)$$ and $$\phi(1,0)=(1,2)$$. Construct an inverse of + linear transformation and observe it carefully. Is it a L.T function + too? + +49. Do you realize the importance of inverting a matrix? + +50. L.T stands for Linear Transformation .It is aka a matrix. + +51. Define a L.T. $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ such that + $$\phi(0,1)=(2,3)$$ and $$\phi(1,0)=(7,4)$$. This function $$\phi$$ is same + as the matrix $$\begin{bmatrix} + 7 & 2 \\ + 4 & 3 + \end{bmatrix}$$. +
$$\phi(x,y)$$ is same as $$\begin{bmatrix} + 7 & 2 \\ + 4 & 3 + \end{bmatrix}$$ $$\begin{bmatrix} + x\\y + \end{bmatrix}$$, Verify and make your share of observations.
+ What is + $$\phi^{-1}$$ ? Is this the traditional matrix inverse? +
Think ! + +52. Consider a L.T. $$\phi$$ such that : $$\phi(1,2)=(3,5)$$ and + $$\phi(3,1)=(8,2)$$. What is the matrix equivalent of $$\phi$$ ? + +53. Solve the following : + - $$\begin{array} 3x-2y=15 \\ x+4y=19 \end{array}$$ + + + - Isn't this the same as $$\begin{bmatrix} + 1 & -2 \\ + 1 & 4 + \end{bmatrix}$$ $$\begin{bmatrix} + x\\y + \end{bmatrix}$$ = $$\begin{bmatrix} + 15\\19 + \end{bmatrix}$$ + + - You are trying to find if there is an element in the domain + which maps to (15,19) . + + - what exactly is happening here ? (Say all that you can) + +
+ +54. Given $$V_{1}$$ , $$V_{2}$$ & $$V_{3}$$ are L.I. , S.T. + + - $$\left \{ V_{2} - V_{3} , V_{1} - V_{3} , V_{1} - V_{2} \right \}$$ + are L.D. + + - $$\left \{ V_{1} + V_{2} , V_{1} + V_{3} , V_{2} + V_{3} \right \}$$ + are L.I. + +55. Given vectors $$\left \{ V_{1} , V_{2} , V_{3} , V_{4} \right \}$$ + their sum is 0 = $$V_{1}$$ + $$V_{2}$$ + $$V_{3}$$ + $$V_{4}$$ . Is this set + L.I or L.D. ? + +56. Show that the following are equivalent: + + - The vectors $$\{v_1,v_2,\dots, v_n\}$$ are linearly independent.
+ + - $$\forall \alpha_1, \alpha_2, \dots, \alpha_n \in \mathbb{R}\ \left( \sum_{i=1}^{n} \alpha_i v_i = 0 \implies \alpha_j = 0\ \forall 1 \leq j \leq n\right)$$.
+ +57. In the following six matrices find out the following: + + 1. Rank of the matrix + + 2. Dimension of the range + + 1. $$\left[ \begin{array}{cc} + 1 & 2\\ 2 & 4 + \end{array}\right]$$ + + 2. $$\left[ \begin{array}{cc} + 1 & 2\\ 3 & 4 + \end{array}\right]$$ + + 3. $$\left[ \begin{array}{cc} + 7 & -7\\ 2 & -2 + \end{array}\right]$$ + + 4. $$\left[ \begin{array}{cc} + 0 & 1\\ 1 & 0 + \end{array}\right]$$ + + 5. $$\left[ \begin{array}{cc} + 1 & 1\\ 3 & 3 + \end{array}\right]$$ + + 6. $$\left[ \begin{array}{ccc} + 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 + \end{array}\right]$$ + + What is happening here? Describe in detail. + +58. The dimension of the range of the matrix $$M$$ and $$M^{T}$$ is always + the same. Why? + +59. Take three linearly independent vectors in $$\mathbb{R}^3$$. Show that + they form a basis of $$\mathbb{R}^3$$. + +60. Consider the matrix $$\left[ \begin{array}{ccc} + 1 & 4 & 7\\ 2 & 5 & 8 \\ 3 & 6 & 9 + \end{array}\right]$$. The dimension of the range is 2. The range of + this linear transformation is obviously a linear combination of + three vectors. Do you see which are those three vectors? + +61. Consider any $$2 \times 2$$ matrix. Do you observe that the : + + Dimension of the Null space & the Dimension of the range are in someway related? + +62. What about a $$3 \times 3$$ matrix? + +63. Can you generalise this to an $$n\times n$$ matrix? + +64. When is a L.T. function one-one and when is it onto? + +65. A $$2\times 2$$ matrix A can be seen as two vectors placed as columns. For + example $$(1,2)$$ and $$(3,4)$$ when placed as columns give rise to the + matrix $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$. + + Note that $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$ $$\begin{bmatrix} + \alpha \\ + \beta + \end{bmatrix}$$ $$\in$$ + $${\{ \alpha(1,2)+\beta(3,4) : \alpha, \beta \in \mathbb{R} \} }$$. + + Note that matrix, $$\begin{bmatrix} + a & b \\ + c & d + \end{bmatrix}$$ $$\begin{bmatrix} + x \\ + y + \end{bmatrix}$$ simply is $$x(a,c)+y(b,d)$$. + + Note that a matrix takes a vector $$(x,y)$$ to a linear combination of + the column vectors. + + It is now clear that the range of the matrix, say$$\begin{bmatrix} + 1 & 1 & 4 \\ + 0 & 2 & 4 \\ + 1 & 3 & 4 + \end{bmatrix}$$ is nothing but the linear combination of the vectors + $$(1,0,1), (1,2,3), (4,4,4)$$. + +66. Consider a $$10\times 10$$ matrix $$A$$, defined as following: + + $$A[i,j] = 0$$ if $$i+j\cong 0(mod2)$$ + + $$A[i,j] = 1$$ if $$i+j\cong 1(mod2)$$ + + What is the dimension of the range? + +67. Consider the sub-space $$S:(y=13x)$$ of $$\mathbb{R}^2$$ + + - Give an example of a $$\phi$$ such that $$S$$ is its null space. + + - Give an example of a $$\phi$$ such that S is the the + range of $$\phi$$. + +68. Let $$A =$$ + $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$ + + - Show that the null space of $$A \subset$$ Null space of $$A^2$$ + + - Is this true for any $$2\times 2$$ matrix. + + - Is this true for any $$3\times3$$ matrix. + + - Is this true for any $$n\times n$$ matrix. + +69. Define column space. S.T. Column space of $$A^2 \subset$$ Column space + of $$A$$. + +70. Solve the following simultaneous equation: +
+ - $$ + \begin{array} _x + 4y + 7z =9\\ + 2x + 5y + 8z = 9\\ + 3x +6y + 9z = 9 + \end{array} + $$ + + - What is the null space of $$\begin{bmatrix} + 1 & 4 & 7 \\ + 2 & 5 & 8 \\ + 3 & 6 & 9 + \end{bmatrix}$$ + - The above two questions are strongly related and + make a theory. What is your obseration? + +71. What does one mean by the linear combination of vectors and what is a + linear span? + +72. Show that, if a matrix $$A$$ has linearly independent column vectors, + then the columns of the matrix $$A^2$$ are also linearly independent. + +73. $$Ax = Ay \iff x=y$$ . Is this true? If False, when is the statement + False and what leads to the falsity of the statement? + +74. Let $$M$$ be a $$3\times 3$$ matrix, such that, the dim(Range) =3. Show + that, $$M^2 = M \iff M$$ is an identity matrix. + +75. Consider a $$10 \times 10$$ matrix with all its entries to be $$1$$. + What is the dimension of its range? + diff --git a/Linalg75.md b/Linalg75.md new file mode 100644 index 0000000..565e1aa --- /dev/null +++ b/Linalg75.md @@ -0,0 +1,454 @@ +--- +layout: page +title: Oceanverse +order: 5 +permalink: /linalg75/ +--- + +* TOC +{:toc} + + +# Linear Algebra + +1. Consider the matrix + $$ + \left[ \begin{array}{cc} + 1 & 2\\ 3 & 4 + \end{array}\right] + $$ + - What does it remind you of? + - What does it denote? + - Where and why do we use a matrix? + - Can you enlist a few applications of matrices? +
+ +2. Define a function. What is a surjective, injective and bijective + function? + +3. Give an example of a function + $$ + f:\mathbb{R}^2\rightarrow\mathbb{R}^2 + $$ + +4. Give an example of a very nice function + $$f:\mathbb{R}^2\rightarrow\mathbb{R}^2$$ + - Make extra efforts to make this function really nice. + - Explain what is so nice about your + function? + - Why should one study such functions? +
+5. Define a function + $$ \phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2 $$, which satisfies the following property: The point $$ \phi(2,3)=(7,4) $$. Note that this function should be defined at all points on $$\mathbb{R}^2$$. + - What are the properties of your function? Observe it + microscopically. +
+ +6. Given a function $$\phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2$$ + which satisfies the following two conditions: + + $$\phi(u+v)=\phi(u) +\phi(v)$$ + + $$\phi(\alpha v)=\alpha\phi(v)$$ + + where $$u=( x_{1} , y_{1} )$$, $$v=( x_{2} , y_{2} )$$ and $$u,v \in \mathbb{R}^2$$ + + * What can one say of such functions? + * Observe this function closely, such functions form the crux of several discplines, mainly of sciences and engineering. Spend at least 20 minutes dissecting them to the best possible extent. +
+8. Consider $$\mathbb{R}^2$$ what are all the properties of this set? + $$\mathbb{R}^2$$ is called a space of all vectors, aka a vector space. + Lookup for the definition of a vector space. + +9. A subset of a vector space which in itself is a vector space is + caled a subspace. Give an example of a subspace of $$\mathbb{R}^2$$. + +10. Given a vector $$(1,7)$$, what does the set + $$\{ \alpha(1,7) | \alpha \in \mathbb{R}\}$$ represent? Is it a + subspace of $$\mathbb{R}^2$$? + +11. Is $$\mathbb{R}^3$$ a vector space? + +12. Conside the two points $$(1,2,3)$$ and $$(4,5,7)\in \mathbb{R}^3$$. What + does the following set denote: + $$\{\alpha(1,2,3)+\beta(4,5,7) | \alpha, \beta \in \mathbb{R}\}$$. + Is this a subspace? + +13. Consider a straight line $$y=2x+1$$ in $$\mathbb{R}^2$$, does it form a + subspace of $$\mathbb{R}^2$$? + +14. Consider a unit circle in $$\mathbb{R}^2$$, centered at origin, is it + a subspace of $$\mathbb{R}^2$$? + +15. What are all the subspaces of $$\mathbb{R}^2$$? + +16. What are all the subspaces of $$\mathbb{R}^3$$? + +17. Given $$\mathbb{R}^3$$, pick any two points $$u,v\in \mathbb{R}^3$$. + Note that $$\{\alpha u+\beta v | \alpha, \beta \in \mathbb{R}\}$$ is a + subspace of $$\mathbb{R}^3$$. Generalize this idea! + +18. The set $$\{\alpha \vec{u} + \beta \vec{v} | \alpha, \beta \in \mathbb{R}\}$$ is + called the linear combination of vectors $$\vec{u}$$ and $$\vec{v}$$. We can + generalize this to $$k$$ vectors. Observe what this set is all about? + +19. We say that a vector $$\vec{w}$$ is manufactured by $$\vec{u}$$ and $$\vec{v}$$ if + $$w\in \{\alpha \vec{u} +\beta \vec{v} | \alpha, \beta \in \mathbb{R} \}$$. + +20. Show that $$(1,2,3)$$ and $$(4,5,6)$$ can manufacture $$(7,8,9)$$. Also + $$(4,5,6)$$ and $$(7,8,9)$$ can manufacture $$(1,2,3)$$. Finally $$(4,5,6)$$ + can be manufactured by the other two vectors. + +21. Can $$(2,1,0)$$ and $$(3,0,8)$$ manufacture $$(1,1,1)$$ ? + +22. Can $$(0,0,1)$$ and $$(0,1,0)$$ manufacture $$(1,0,0)$$? + +23. When can two vectors in $$\mathbb{R}^3$$ manufacture a given third + vector? + +24. When can two vectors in $$\mathbb{R}^3$$ fail to manufacture a given + third vector? + +25. If $$\{\vec{u},\vec{v},\vec{w}\}$$ are such that a vector in this set can be + manufactured by some vectors in the same set, then such a set is + called a linearly dependent set. + +26. Give examples of a linearly dependent set in $$\mathbb{R}^3$$ and get + conversant with the definition. + +27. If $$\{\vec{u},\vec{v},\vec{w}\}$$ are such that no vector in this set can be + manufactured by any combination of vectors in the same set, then such + a set is called a linearly independent set. + +28. Give examples of a linearly dependent set in $$\mathbb{R}^3$$ and + $$\mathbb{R}^2$$ and get conversant with the definition. + +29. Are $$(1,2), (3,4)$$ linearly independent in $$\mathbb{R}^2$$? Prove! + +30. Are $$(1,1),(2,3),(7,17)$$ Linearly Independent or Dependent? + +31. - Construct a set of 3 vectors that are Linearly Independent in + $$\mathbb{R}^2$$. Can you? + + - Construct a set of 3 vectors that are Linearly Independent in + $$\mathbb{R}^3$$. Can you? + + - Construct a set of $$k$$ vectors that are Linearly Independent in + $$\mathbb{R}^k$$. Can you? + + - Construct a set of $$k+1$$ vectors that are Linearly Independent in + $$\mathbb{R}^k$$. Can you? + +32. - Show that in $$\mathbb{R}^2$$ we can at most have 2 Linearly + Independent vectors. + + - Show that in $$\mathbb{R}^3$$ we can at most have 3 Linearly + Independent vectors. + + - Show that in $$\mathbb{R}^n$$ we can at most have $$n$$ Linearly + Independent vectors. + +33. Set of any two linearly independent vectors in $$\mathbb{R}^2$$ is + called a basis. Set of any three linearly independent vectors in + $$\mathbb{R}^3$$ is called a basis. Similarly, for $$n$$. + +34. Show that a basis can manufacture any vector of the vector + space. + +35. Show that any set of linearly independent vectors form a subset of + some basis. In other words, one can include a few more elements to a + linearly independent set and make it a basis. + +36. Show that the number of elements in any basis for a given vector + space is always constant. + +37. Try taking a few vectors in $$\mathbb{R}^3$$ and discuss its linear + independence or linear dependence. Try atleast 10 examples and + familiarize yourself. + +38. Show that any 3 vectors on a plane passing through the origin in + $$\mathbb{R}^3$$ cannot be linearly independent. Prove. + +39. What are all the subspaces of $$R^3$$. + +40. Consider a subspace of $$R^3$$ and write down its basis. Do this for 3 + to 4 different subspaces. + +41. Give an example of a function + $$f:\mathbb{R}^2 \rightarrow \mathbb{R}^2$$ such that the range of the + function is the straight line $$y=10x$$. + +42. As an example consider the following basis set of + $$\mathbb{R}^2 : \left \{(1,2),(2,2)\right \}$$. Construct a function + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ such that: + + $$\phi(\vec{u}+\vec{v})=\phi(\vec{u})+\phi(\vec{v})$$ + + $$\phi(\alpha \vec{u})= \alpha \phi(\vec{u})$$ + + Such a function is called a LT function, + + - Where is (1,2) and (2,2) mapped? + + - Where is (1,0) and (0,1) mapped? + + - What is the range of this function? + +43. Consider a function $$\phi$$ which is LT which maps + + $$\phi(1,2)=(3,4)$$ + + $$\phi(6,6)= (2,0)$$ + + - How many such functions can you construct? + + - What is the range of this function? + +44. Discuss the range of the following functions, given their values at + a few points: + + $$\phi(1,2)=(3,4)$$ $$\&$$ $$\phi(1,1)=(6,8)$$ + + $$\phi(1,1)=(2,2)$$ $$\&$$ $$\phi(3,3)=(4,4)$$ + + $$\phi(1,2)=(3,5)$$ $$\&$$ $$\phi(0,8)=(3,0)$$ + + $$\phi(-2,2)=(0,0)$$ $$\&$$ $$\phi(8,2)=(1,1)$$ + + $$\phi(1,1)=(2,2)$$ $$\&$$ $$\phi(1,2)=(3,3)$$ + +45. Give an example of an LT function which maps a L.I. set of vectors + to a L.I. set of vectors i.e. + $$\phi:\mathbb{R}^2 \rightarrow \mathbb{R}^2$$, where + $$\left \{ \vec{u},\vec{v} \right \}$$ are L.I. $$\&$$ + $$\left \{\phi(\vec{u}), \phi(\vec{v})\right \}$$ are also L.I. + +46. Same as the previous question, but $$\left \{ \vec{u},\vec{v} \right \}$$ is L.I. + and $$\left \{\phi(\vec{u}), \phi(\vec{v})\right \}$$ is L.D.\ + What can one say about the range? + +47. Note that range of a L.I function is always a subspace. + +48. Note that the set N=$$\{\vec{v}: \phi(\vec{v})=0\}$$ is a subspace of $$R^2$$ where + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ is L.I . Take atleast 5 + different examples of L.I functions and see if this is true. The set + $$N\subseteq Domain$$ is called the null space of $$\phi$$. + +49. Construct a Linear Transformation + $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$, + $$\phi(0,1)=(3,4)$$ and $$\phi(1,0)=(1,2)$$. Construct an inverse of + linear transformation and observe it carefully. Is it a L.T function + too? + +50. Do you realize the importance of inverting a matrix? + +51. L.T stands for Linear Transformation .It is aka a matrix. + +52. Define a L.T. $$\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2$$ such that + $$\phi(0,1)=(2,3)$$ and $$\phi(1,0)=(7,4)$$. This function $$\phi$$ is same + as the matrix $$\begin{bmatrix} + 7 & 2 \\ + 4 & 3 + \end{bmatrix}$$. +
$$\phi(x,y)$$ is same as $$\begin{bmatrix} + 7 & 2 \\ + 4 & 3 + \end{bmatrix}$$ $$\begin{bmatrix} + x\\y + \end{bmatrix}$$, Verify and make your share of observations.
+ What is + $$\phi^{-1}$$ ? Is this the traditional matrix inverse? +
Think ! + +53. Consider a L.T. $$\phi$$ such that : $$\phi(1,2)=(3,5)$$ and + $$\phi(3,1)=(8,2)$$. What is the matrix equivalent of $$\phi$$ ? + +54. Solve the following : + - $$\begin{array} 3x-2y=15 \\ x+4y=19 \end{array}$$ + + + - Isn't this the same as $$\begin{bmatrix} + 1 & -2 \\ + 1 & 4 + \end{bmatrix}$$ $$\begin{bmatrix} + x\\y + \end{bmatrix}$$ = $$\begin{bmatrix} + 15\\19 + \end{bmatrix}$$ + + - You are trying to find if there is an element in the domain + which maps to (15,19) . + + - what exactly is happening here ? (Say all that you can) + +
+ +55. Given $$\overrightarrow{V}_{1}$$ , $$\overrightarrow{V}_{2}$$ & $$\overrightarrow{V}_{3}$$ are L.I. , S.T. + + - $$\left \{ \overrightarrow{V}_{2} - \overrightarrow{V}_{3} , \overrightarrow{V}_{1} - \overrightarrow{V}_{3} , \overrightarrow{V}_{1} - \overrightarrow{V}_{2} \right \}$$ + are L.D. + + - $$\left \{ \overrightarrow{V}_{1} + \overrightarrow{V}_{2} , \overrightarrow{V}_{1} + \overrightarrow{V}_{3} , \overrightarrow{V}_{2} + \overrightarrow{V}_{3} \right \}$$ + are L.I. + +56. Given vectors $$\left \{ \overrightarrow{V}_{1} , \overrightarrow{V}_{2} , \overrightarrow{V}_{3} , \overrightarrow{V}_{4} \right \}$$ + their sum is 0 = $$\overrightarrow{V}_{1}$$ + $$\overrightarrow{V}_{2}$$ + $$\overrightarrow{V}_{3}$$ + $$\overrightarrow{V}_{4}$$ . Is this set + L.I or L.D. ? + +57. Show that the following are equivalent: + + - The vectors $$\{\vec{v}_1,\vec{v}_2,\dots, \vec{v}_n\}$$ are linearly independent.
+ + - $$\forall \alpha_1, \alpha_2, \dots, \alpha_n \in \mathbb{R}\ \left( \sum_{i=1}^{n} \alpha_i \vec{v}_i = 0 \implies \alpha_j = 0\ \forall 1 \leq j \leq n\right)$$.
+ +58. In the following six matrices find out the following: + + 1. Rank of the matrix + + 2. Dimension of the range + + 1. $$\left[ \begin{array}{cc} + 1 & 2\\ 2 & 4 + \end{array}\right]$$ + + 2. $$\left[ \begin{array}{cc} + 1 & 2\\ 3 & 4 + \end{array}\right]$$ + + 3. $$\left[ \begin{array}{cc} + 7 & -7\\ 2 & -2 + \end{array}\right]$$ + + 4. $$\left[ \begin{array}{cc} + 0 & 1\\ 1 & 0 + \end{array}\right]$$ + + 5. $$\left[ \begin{array}{cc} + 1 & 1\\ 3 & 3 + \end{array}\right]$$ + + 6. $$\left[ \begin{array}{ccc} + 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 + \end{array}\right]$$ + + What is happening here? Describe in detail. + +59. The dimension of the range of the matrix $$M$$ and $$M^{T}$$ is always + the same. Why? + +60. Take three linearly independent vectors in $$\mathbb{R}^3$$. Show that + they form a basis of $$\mathbb{R}^3$$. + +61. Consider the matrix $$\left[ \begin{array}{ccc} + 1 & 4 & 7\\ 2 & 5 & 8 \\ 3 & 6 & 9 + \end{array}\right]$$. The dimension of the range is 2. The range of + this linear transformation is obviously a linear combination of + three vectors. Do you see which are those three vectors? + +62. Consider any $$2 \times 2$$ matrix. Do you observe that the : + + Dimension of the Null space & the Dimension of the range are in someway related? + +63. What about a $$3 \times 3$$ matrix? + +64. Can you generalise this to an $$n\times n$$ matrix? + +65. When is a L.T. function one-one and when is it onto? + +66. A $$2\times 2$$ matrix A can be seen as two vectors placed as columns. For + example $$(1,2)$$ and $$(3,4)$$ when placed as columns give rise to the + matrix $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$. + + Note that $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$ $$\begin{bmatrix} + \alpha \\ + \beta + \end{bmatrix}$$ $$\in$$ + $${\{ \alpha(1,2)+\beta(3,4) : \alpha, \beta \in \mathbb{R} \} }$$. + + Note that matrix, $$\begin{bmatrix} + a & b \\ + c & d + \end{bmatrix}$$ $$\begin{bmatrix} + x \\ + y + \end{bmatrix}$$ simply is $$x(a,c)+y(b,d)$$. + + Note that a matrix takes a vector $$(x,y)$$ to a linear combination of + the column vectors. + + It is now clear that the range of the matrix, say$$\begin{bmatrix} + 1 & 1 & 4 \\ + 0 & 2 & 4 \\ + 1 & 3 & 4 + \end{bmatrix}$$ is nothing but the linear combination of the vectors + $$(1,0,1), (1,2,3), (4,4,4)$$. + +67. Consider a $$10\times 10$$ matrix $$A$$, defined as following: + + $$A[i,j] = 0$$ if $$i+j\cong 0(mod2)$$ + + $$A[i,j] = 1$$ if $$i+j\cong 1(mod2)$$ + + What is the dimension of the range? + +68. Consider the sub-space $$S:(y=13x)$$ of $$\mathbb{R}^2$$ + + - Give an example of a $$\phi$$ such that $$S$$ is its null space. + + - Give an example of a $$\phi$$ such that $$S$$ is the the + range of $$\phi$$. + +69. Let $$A =$$ + $$\begin{bmatrix} + 1 & 3 \\ + 2 & 4 + \end{bmatrix}$$ + + - Show that the null space of $$A \subset$$ Null space of $$A^2$$ + + - Is this true for any $$2\times 2$$ matrix. + + - Is this true for any $$3\times3$$ matrix. + + - Is this true for any $$n\times n$$ matrix. + +70. Define column space. S.T. Column space of $$A^2 \subset$$ Column space + of $$A$$. + +71. Solve the following simultaneous equation: +
+ - $$ + \begin{array} _x + 4y + 7z =9\\ + 2x + 5y + 8z = 9\\ + 3x +6y + 9z = 9 + \end{array} + $$ + + - What is the null space of $$\begin{bmatrix} + 1 & 4 & 7 \\ + 2 & 5 & 8 \\ + 3 & 6 & 9 + \end{bmatrix}$$ + - The above two questions are strongly related and + make a theory. What is your obseration? + +72. What does one mean by the linear combination of vectors and what is a + linear span? + +73. Show that, if a matrix $$A$$ has linearly independent column vectors, + then the columns of the matrix $$A^2$$ are also linearly independent. + +74. $$A\vec{x} = A\vec{y} \iff \vec{x}=\vec{y}$$ . Is this true? If False, when is the statement + False and what leads to the falsity of the statement? + +75. Let $$M$$ be a $$3\times 3$$ matrix, such that, the dim(Range) =3. Show + that, $$M^2 = M \iff M$$ is an identity matrix. + +76. Consider a $$10 \times 10$$ matrix with all its entries to be $$1$$. + What is the dimension of its range? diff --git a/Links.md b/Links.md new file mode 100644 index 0000000..26d95eb --- /dev/null +++ b/Links.md @@ -0,0 +1,12 @@ +--- +layout: page +title: Links +permalink: /links/ +order: 3 +--- + +1. Watch [these videos](https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab) without fail. This is a good intuitive introduction to linear algebra. + +2. These [Videos](https://www.youtube.com/playlist?list=PLZHQObOWTQDMsr9K-rj53DwVRMYO3t5Yr) make an essential introduction to calculus. + +3. [Here](https://www.youtube.com/watch?v=QVKj3LADCnA&list=PL49CF3715CB9EF31D) is a complete course on linear algebra from MIT OCW. It is the most popular resource for the subject. diff --git a/Oceanverse.md b/Oceanverse.md new file mode 100644 index 0000000..fb34e3b --- /dev/null +++ b/Oceanverse.md @@ -0,0 +1,184 @@ +--- +layout: page +title: Oceanverse +order: 5 +permalink: /oceanverse/ +--- + +* TOC +{:toc} + +# Ocean Part 1 + +1\. Write a program that prints "Namasthey India" to the screen (1 point). + +2\. Take as input a number $$n$$ and print the square, cube and $$2^n$$ of the number (1 point). + +3\. Print the following using four print statements: +``` +* +** +*** +**** +``` +(1 point) . + +4\. Write an interactive python program which does the following: +``` +What's your name? John +How old are you? 25 +What's your favorite color? Blue +What's your favorite hobby? Reading +``` +(1 point). + +5\. Understand how to use a ```if conditional``` in python. Ask the user to enter a number and check if the number is even or odd (1 point). + +6\. Write a program to take as input a number $$n$$ and display the first $$n$$ natural numbers (1 point). + +7\. Print a sequence of numbers starting from the number **a** with common difference **d**. Go on till you reach the number **b**. +``` +Enter a value for a: 10 +Enter a value for d: 3 +Enter a value for b: 20 +Output: 10 13 16 19 +``` +(1 point). + +8\. Write a program that calculates and prints the sum of all numbers from 1 to n, where n is provided by the user (1 point). + +9\. Write a program that takes a number n from the user and prints the multiplication table for that number from 1 to 10. Generalize it from $$i$$ to $$j$$. +``` +2X1=2 +2X2=4 +and so on... +``` +(1 point). + +10\. Write a program to find out if the given number is prime or not (1 point). + +# Ocean Part 2 + +11\. Write a program to take as input $$n$$ and print all prime numbers upto and including $$n$$ (1 point). + +12\. Input two different strings and concatenate it (1 point). + +13\. Take two strings of the same length and intersperse the second one into the first one: +``` +Input: +india +super +Output: +isnudpiear +``` +(1 point). + +14\. Given a string, write a program to reverse it (1 point). + +15\. Given a string, check if it is a palindrome or not (1 point). + +16\. Write a program that counts and prints the number of vowels and the number of consonants in the string (1 point). + +17\. List of Squares: Write a program that prints the square of numbers from 1 to n, where n is provided by the user (1 point). + +18\. Fibonacci Sequence : Write a program that prints the first n numbers in Fibonacci numbers (1 point). + +19\. Print Star Pattern: Write a program that takes a number n from the user and prints a right-angled triangle pattern with stars of n rows (1 point) . + +20\. Write a piece of code which does exactly as specified in [this video](https://www.youtube.com/watch?v=JA_70M-ma-k) (10 points). + +21\. Factorial: Write a program that calculates the factorial of a number provided by the user (1 point). + +22\. Positive or Negative: Write a program that asks the user for a number and prints whether the number is positive, negative, or zero (1 point). + +23\. Simple Interest Calculation: Write a program that calculates the simple interest for given principal, rate, and time provided by the user (1 point). + +24\. Temperature Converter: Write a program that converts Celsius to Fahrenheit or Fahrenheit to Celsius, depending on user input (1 point). + +25\. Leap Year or Not: Write a program that checks if a given year is a leap year or not. Google for the details on how to figure out if the given number is a leap year or not. It is more complicated than simply checking for a multiple of 4 (1 point). + +26\. Divisible by 7 and 5: Write a program that checks if a number provided by the user is divisible by both 7 and 5. Generalize it to a and b (1 point). + +27\. Create a Python program that prompts the user for their age. If the age is less than 18, print "You are a minor." If the age is between 18 and 65, print "You are an adult." Otherwise, print "You are a senior citizen." (1 point). + +28\. Grading System: Write a program that takes the marks of five subjects from the user and calculates the grade according to the average marks: +A if average >= 90 +B if average >= 80 and < 90 +C if average >= 70 and < 80 +D if average >= 60 and < 70 +F otherwise +(1 point). + +29\. Decimal to Binary Conversion: Write a program that converts a decimal number to its binary representation using loops, without using built-in conversion functions (1 point). + +30\. Write a program that finds the gcd of two numbers using Euclid's Algrorithm. Given $$k$$ as an input, display those two numbers, both with $$k$$ digits, such that they take the maximum number of steps to find the GCD, across all the pair of numbers, both of which are of $$k$$ digits (8 points). + +31\. Write a program to populate a list $$L$$ with the first $$n$$ natural numbers (1 point). + +32\. Write a program to populate a list $$L$$ with random numbers in the range 1 to 1000 (1 point). + + + +# Ocean Part 3 +(Watch [these](https://www.youtube.com/watch?v=8ndsDXohLMQ&list=PLDsnL5pk7-N_9oy2RN4A65Z-PEnvtc7rf) videos, as and when required) + +33\. Write a function called `add` that takes two numbers as arguments and returns their sum. (1 point) + +34\. Write a function called `factorial` that takes an integer `n` and returns the factorial of `n`. (1 point) + +35\. Write a function called `fibonacci` that takes an integer `n` and returns the `n`-th number in the Fibonacci sequence. (1 point) + +36\. Write a function which simulates the process of throwing $$n$$ identical balls into $$n$$ bins. What is the maximum across the buckets? Write a short report on the output of your code. (2 points) + +37\. Write a function which simulates the process of throwing identical balls into $$n$$ identical bins until all the bins are non-empty. How many balls are we expected to throw? Investigate and write a short report based on your observation. (2 points) + +38\. Checking for Even or Odd: Write a function called `is_even` that takes an integer and returns `True` if the number is even, and `False` if it is odd. (1 point) + +39\. Calculate Area of a Circle: Write a function called `circle_area` that takes the radius of a circle as an argument and returns its area. (1 point) + +40\. Write a function that displays the spiral: RULLDDRRRUUULLLL... and so on. It should keep displaying until it has displayed 1,000,000 Letters in this pattern. (5 points) + +41\. Concatenating Strings: Write a function called `concatenate` that takes two strings and returns them concatenated together with a space between them. (1 point) + +42\. Finding the Maximum: Write a function called `find_max` that takes a list of numbers and returns the largest number in the list. (1 point) + +43\. Consider the sensex data from [here](https://www.kaggle.com/code/kerneler/starter-bse-sensex-index-30-yrs-111d3b62-d/input). Consider only the end of the day closing values. When should you have bought and when should you have sold in order to gain the maximum return in this 30 year period? You can assume that you can buy the stocks partially and you start with, let us say 1,00,000 Rupees. (10 points) + +44\. Consider the data of Height and Weight of 25,000 people as available [here](https://www.kaggle.com/datasets/burnoutminer/heights-and-weights-dataset). Is the data correlated? What is the correlation? Can you plot the points and fit a line? You are free to use any built in functions, but you should know what the functions are doing. Correlation is a statistical concept which you may know from your high school, we only expect you to understand this concept at an intuitive level. (5 point) + +# Ocean Part 4 + +45\. Reading exercise (first few chapters of Algorithms to live by). (25 points) + +46\. Write a function that takes as inputs list of lists that depicts square matrices A and B and then gives us the sum. (1 point) + +47\. Write a function that takes as inputs list of lists that depicts square matrices A and B and then gives us the product. (2 points) + +48\. Write a function that writes the first n numbers and writes it to a file by name output.txt (1 point) + +49\. Write a function that reads a file which has numbers in each line and outputs it on the screen one by one. (1 point) + + +50\. Solve [this](https://drive.google.com/file/d/1YiWz-QLg95ru2LljxvL8vHNLOErDUurr/view?usp=sharing) question. (10 points) + +51\. Write a program to sort a list of numbers using the bubble sort technique. (1 point) + +52\. Write a program to sort a list of numbers using the merge sort technique. (2 point) + +53\. Write a program to sort a list of numbers using the quick sort technique. (2 point) + +54\. Write a program to search for an element in a list using Binary Search.(2 point) + +55\. Write a program which, given a text file comprising of all words in lower case, one word per line, sorts this file using bubble sort, merge sort and quick sort. Which technique is the fastest and why? Write a detailed report. (5 points) + +56\. Write a program to find the median element in a list of unsorted elements. You are not supposed to sort the list. (2 points) + +57\. Solve the [contiguous sum sub array problem](https://en.wikipedia.org/wiki/Maximum_subarray_problem) (1 point). + +58\. We solved the SFC question a while ago. Can you solve [this](https://en.wikipedia.org/wiki/Peano_curve) on similar lines? (2 points) + +59\. Write a program to encrypt a string using [caesar cipher](https://en.wikipedia.org/wiki/Caesar_cipher). (1 point) + +60\. [Read and Solve this](https://docs.google.com/document/d/1ywkFHqGTvNHREsTz-40V75DefmPYYKoPkd1aAMfPVpA/edit?usp=sharing) (20 points) + + diff --git a/Pagerank.md b/Pagerank.md new file mode 100644 index 0000000..797fa9f --- /dev/null +++ b/Pagerank.md @@ -0,0 +1,26 @@ +--- +layout: page +title: Pagerank +order: 5 +permalink: /pagerank/ +--- + +1. Consider any $$2\times 2$$ matrix A and apply the matrix on a $$2\times1$$ vector $$v$$. Keep applying this matrix and notice that the direction converges, while the magnitude may get larger. Keep normalizing $$v$$ and notice the direction to which it converges. Use Numpy +1. Consider the previous $$2\times 2$$ matrix and find out its eigenvalue and eigenvectors. What do you observe? + +3. 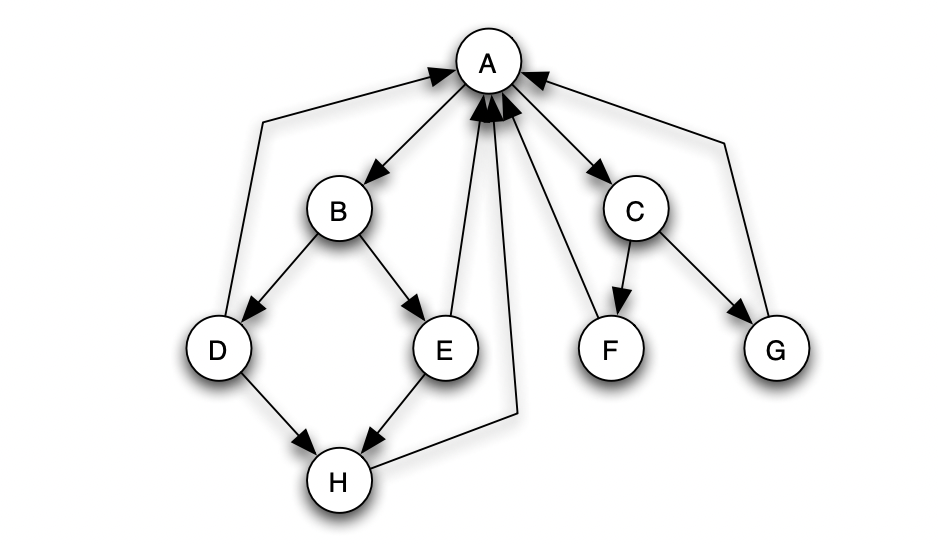Consider the following network: + ![Network](https://sudarshansudarshan.github.io/cs522/files/pagerank_example.png)Assign values to the nodes so that the value of the nodes = sum of the values of the nodes from which there are incoming edges. For example the value of F should be half of the value of C. The value of E should be half the value of B and so on. + +4. Write down the edge list of the above graph and use networkx to run a random walk on it. What is the distribution of visits? + +5. Are the following two questions equivalent?: + + - If I were to give pocket money to two of my daughters: 500 rupees each. + + - I toss a coin and give my elder daughter 1000 rupees if its heads or the younger daughter 1000 rupees if its tails. + + Are these two statements equivalent? In the sense that, by the end of the year, do you think both my daughters would have received, more or less, the same amount of money? + +6. Consider the adjacency matrix of the above graph, tweak it and observe that the _principal eigen vector_ is same as the answer to the previous question. (Principal Eigen Vector is defined as the eigen vector corresponding to the highest eigen value) + +7. Can you consider a network of vertices, in the order of thousands and figure out the answer? You will observe that the best method to use is the random walk (with teleportation). why? diff --git a/Questions.md b/Questions.md new file mode 100644 index 0000000..4a1bd2d --- /dev/null +++ b/Questions.md @@ -0,0 +1,69 @@ +--- +layout: page +title: Questionverse +order: 5 +permalink: /questionverse +--- + +# Chapter 1: Warmup + +1. What is the intuition for this infinite series being equal to 1? $$ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots$$ + +2. Fact: $$ \frac{1}{1-x} = 1+x+x^2+x^3+\dots $$. Is this always true? + +3. Note that $$ e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!}\dots $$. Why is this number important? Can you notice that this number is obviously greater than 1? Can you show that it is actually less than 3? + +4. Note that $$ e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!}\dots $$. What is the significance of this? + +5. Understand Binomial Theorem and show that $$ \left( 1+\frac{1}{n}\right)^n = e) $$ + +6. If you keep compounding your money, when will it get doubled? (Hint: $$ \left( 1+\frac{1}{n}\right)^n = e) $$) + +7. If you keep spending your money by $$\epsilon$$ proportion, when will your money get to less than a rupee? + +8. If you consider a 1000 meter long stick and randomly break it at some point, what do you expect the length to be, of the smaller part and the bigger part? + +9. A bus conductor charges 1000 rupees per seat. The bus can accommodate 100 people. If $$k$$ number of seats are empty, the conductor levies a penalty of $$10k$$ on each passenger. For example, if 5 seats are empty, the conductor will charge 1050 for the 95 passengers who are present. What is the number of passengers for which the conductor earns the maximum money? + +10. Understand the Monty Hall problem. + +11. What is the importance of a matrix? Where do we use them? + +12. What is the intuitive idea of an inverse of a matrix? + +13. In the following code, what is the probability that $$a$$, $$b$$ and $$c$$ form the sides of a triangle? + + ```python + import random + a=random.random() + b=random.random() + c=random.random() + ``` + +14. Show that $$sqrt(2)$$ is irrational. + +15. Show that prime numbers are infinite. + +16. You know the old school way of adding, subtracting, multiplying and dividing 2 big numbers. Can you provide a proof for these methods? + +17. Find the GCD of two big numbers using only a calculator. What method helps you calculate the GCD fast? How do you know that the method works? Can you figure out the number of steps it takes to arrive at a solution? + +18. Describe Birthday Paradox. Write a piece of python code to figure out the probability of you finding same birthdays in a class of $$n$$ people. Plot the probability on the $$Y$$ axis and the number of people in the class $$n$$ in the $$X$$ axis. How does the curve look like? + +19. After programmatically understanding the birthday paradox, can you understand it mathematically? + +20. When you distribute $$n$$ chocolates to $$n$$ people uniformly at random, many of them may end up getting more than one chocolate. How many people, on an average, end up getting no chocolates at all. + + + + + + + + + + + diff --git a/README.md b/README.md index 4581ae8..1f5f137 100644 --- a/README.md +++ b/README.md @@ -1,2 +1,220 @@ -# aicamp -This is a homepage for the AI Vicharana Shala Summer Camp at IIT Ropar 2024 +# minima + +*Minima is a one-size-fits-all Jekyll theme for writers*. It's Jekyll's default (and first) theme. It's what you get when you run `jekyll new`. + +[Theme preview](https://jekyll.github.io/minima/) + +![minima theme preview](/screenshot.png) + +$$a^2$$ + +## Installation + +Add this line to your Jekyll site's Gemfile: + +```ruby +gem "minima" +``` + +And add this line to your Jekyll site: + +```yaml +theme: minima +``` + +And then execute: + + $ bundle + + +## Contents At-A-Glance + +Minima has been scaffolded by the `jekyll new-theme` command and therefore has all the necessary files and directories to have a new Jekyll site up and running with zero-configuration. + +### Layouts + +Refers to files within the `_layouts` directory, that define the markup for your theme. + + - `default.html` — The base layout that lays the foundation for subsequent layouts. The derived layouts inject their contents into this file at the line that says ` {{ content }} ` and are linked to this file via [FrontMatter](https://jekyllrb.com/docs/frontmatter/) declaration `layout: default`. + - `home.html` — The layout for your landing-page / home-page / index-page. [[More Info.](#home-layout)] + - `page.html` — The layout for your documents that contain FrontMatter, but are not posts. + - `post.html` — The layout for your posts. + +### Includes + +Refers to snippets of code within the `_includes` directory that can be inserted in multiple layouts (and another include-file as well) within the same theme-gem. + + - `disqus_comments.html` — Code to markup disqus comment box. + - `footer.html` — Defines the site's footer section. + - `google-analytics.html` — Inserts Google Analytics module (active only in production environment). + - `head.html` — Code-block that defines the `` in *default* layout. + - `header.html` — Defines the site's main header section. By default, pages with a defined `title` attribute will have links displayed here. + +### Sass + +Refers to `.scss` files within the `_sass` directory that define the theme's styles. + + - `minima.scss` — The core file imported by preprocessed `main.scss`, it defines the variable defaults for the theme and also further imports sass partials to supplement itself. + - `minima/_base.scss` — Resets and defines base styles for various HTML elements. + - `minima/_layout.scss` — Defines the visual style for various layouts. + - `minima/_syntax-highlighting.scss` — Defines the styles for syntax-highlighting. + +### Assets + +Refers to various asset files within the `assets` directory. +Contains the `main.scss` that imports sass files from within the `_sass` directory. This `main.scss` is what gets processed into the theme's main stylesheet `main.css` called by `_layouts/default.html` via `_includes/head.html`. + +This directory can include sub-directories to manage assets of similar type, and will be copied over as is, to the final transformed site directory. + +### Plugins + +Minima comes with [`jekyll-seo-tag`](https://github.com/jekyll/jekyll-seo-tag) plugin preinstalled to make sure your website gets the most useful meta tags. See [usage](https://github.com/jekyll/jekyll-seo-tag#usage) to know how to set it up. + +## Usage + +### Home Layout + +`home.html` is a flexible HTML layout for the site's landing-page / home-page / index-page.
+ +#### Main Heading and Content-injection + +From Minima v2.2 onwards, the *home* layout will inject all content from your `index.md` / `index.html` **before** the **`Posts`** heading. This will allow you to include non-posts related content to be published on the landing page under a dedicated heading. *We recommended that you title this section with a Heading2 (`##`)*. + +Usually the `site.title` itself would suffice as the implicit 'main-title' for a landing-page. But, if your landing-page would like a heading to be explicitly displayed, then simply define a `title` variable in the document's front matter and it will be rendered with an `

` tag. + +#### Post Listing + +This section is optional from Minima v2.2 onwards.
+It will be automatically included only when your site contains one or more valid posts or drafts (if the site is configured to `show_drafts`). + +The title for this section is `Posts` by default and rendered with an `

` tag. You can customize this heading by defining a `list_title` variable in the document's front matter. + +-- + +### Customization + +To override the default structure and style of minima, simply create the concerned directory at the root of your site, copy the file you wish to customize to that directory, and then edit the file. +e.g., to override the [`_includes/head.html `](_includes/head.html) file to specify a custom style path, create an `_includes` directory, copy `_includes/head.html` from minima gem folder to `/_includes` and start editing that file. + +The site's default CSS has now moved to a new place within the gem itself, [`assets/main.scss`](assets/main.scss). To **override the default CSS**, the file has to exist at your site source. Do either of the following: +- Create a new instance of `main.scss` at site source. + - Create a new file `main.scss` at `/assets/` + - Add the frontmatter dashes, and + - Add `@import "minima";`, to `/assets/main.scss` + - Add your custom CSS. +- Download the file from this repo + - Create a new file `main.scss` at `/assets/` + - Copy the contents at [assets/main.scss](assets/main.scss) onto the `main.scss` you just created, and edit away! +- Copy directly from Minima 2.0 gem + - Go to your local minima gem installation directory ( run `bundle show minima` to get the path to it ). + - Copy the `assets/` folder from there into the root of `` + - Change whatever values you want, inside `/assets/main.scss` + +-- + +### Customize navigation links + +This allows you to set which pages you want to appear in the navigation area and configure order of the links. + +For instance, to only link to the `about` and the `portfolio` page, add the following to you `_config.yml`: + +```yaml +header_pages: + - about.md + - portfolio.md +``` + +-- + +### Change default date format + +You can change the default date format by specifying `site.minima.date_format` +in `_config.yml`. + +``` +# Minima date format +# refer to http://shopify.github.io/liquid/filters/date/ if you want to customize this +minima: + date_format: "%b %-d, %Y" +``` + +-- + +### Enabling comments (via Disqus) + +Optionally, if you have a Disqus account, you can tell Jekyll to use it to show a comments section below each post. + +To enable it, add the following lines to your Jekyll site: + +```yaml + disqus: + shortname: my_disqus_shortname +``` + +You can find out more about Disqus' shortnames [here](https://help.disqus.com/customer/portal/articles/466208). + +Comments are enabled by default and will only appear in production, i.e., `JEKYLL_ENV=production` + +If you don't want to display comments for a particular post you can disable them by adding `comments: false` to that post's YAML Front Matter. + +-- + +### Social networks + +You can add links to the accounts you have on other sites, with respective icon, by adding one or more of the following options in your config: + +```yaml +twitter_username: jekyllrb +github_username: jekyll +dribbble_username: jekyll +facebook_username: jekyll +flickr_username: jekyll +instagram_username: jekyll +linkedin_username: jekyll +pinterest_username: jekyll +youtube_username: jekyll +googleplus_username: +jekyll +rss: rss + +mastodon: + - username: jekyll + instance: example.com + - username: jekyll2 + instance: example.com +``` + +-- + +### Enabling Google Analytics + +To enable Google Analytics, add the following lines to your Jekyll site: + +```yaml + google_analytics: UA-NNNNNNNN-N +``` + +Google Analytics will only appear in production, i.e., `JEKYLL_ENV=production` + +-- + +### Enabling Excerpts on the Home Page + +To display post-excerpts on the Home Page, simply add the following to your `_config.yml`: + +```yaml +show_excerpts: true +``` + +## Contributing + +Bug reports and pull requests are welcome on GitHub at https://github.com/jekyll/minima. This project is intended to be a safe, welcoming space for collaboration, and contributors are expected to adhere to the [Contributor Covenant](http://contributor-covenant.org) code of conduct. + +## Development + +To set up your environment to develop this theme, run `script/bootstrap`. + +To test your theme, run `script/server` (or `bundle exec jekyll serve`) and open your browser at `http://localhost:4000`. This starts a Jekyll server using your theme and the contents. As you make modifications, your site will regenerate and you should see the changes in the browser after a refresh. + +## License + +The theme is available as open source under the terms of the [MIT License](http://opensource.org/licenses/MIT). diff --git a/Syllabus.md b/Syllabus.md new file mode 100644 index 0000000..249ec83 --- /dev/null +++ b/Syllabus.md @@ -0,0 +1,29 @@ +--- +layout: page +title: Syllabus +permalink: /syllabus/ +order: 7 +--- +The following syllabus is only indicative of the topics we will be covering. We may not follow this sequence. The teaching style will be _illustrative_ and not _enumerative_. + +| Sl. No. | Topic | +| ------- | ------------------------------------------------------------ | +| 1 | Introduction to Mathematical Thinking | +| 2 | A Gentle Introduction to Probability | +| 3 | Random Variables and Expectations | +| 4 | Distributions: Binomial, Bernoulli, Gaussian & Poisson | +| 5 | Markov Chains | +| 6 | Introduction to Matrices | +| 7 | Linearly Independent and Dependent Vectors | +| 8 | Linear Transformations | +| 9 | Matrix Factorization | +| 10 | Applications: Dimensionality Reduction, Recommender Systems, Pagerank, Support Vector Machines | + + + + + + + + + diff --git a/Todo.md b/Todo.md new file mode 100644 index 0000000..aa5cdcf --- /dev/null +++ b/Todo.md @@ -0,0 +1,30 @@ +--- +layout: page +title: Todo +permalink: /todo/ +--- + +@TAs + +Note: Leave it to me if you cannot cover some of the topics. + +# ToDo for TAs + +1. Session on basic probability (absolute minimals). +2. Session on functions. How to find minima/maxima of a function. +3. Session on Geogebra. +4. Teach them: + - Matrix multiplication. + - Determinants. + - Geometrical meaning of dot product. + - Matrix Inverse. + - Finding Eigen Values and Eigen Vectors. + (All of these should be for 2x2 matrices only). + Refer to 3blue1brown's youtube channel. Refer to his linear algebra vidoes. They are short and sweet. + +# Project Component +There is a project for 10 marks. Feel free to give them some reading or programming assignment based on the math concepts taught. + +Regards, +Sudarshan + diff --git a/_config.yml b/_config.yml new file mode 100644 index 0000000..680f2f4 --- /dev/null +++ b/_config.yml @@ -0,0 +1,74 @@ +# Welcome to Jekyll! +# +# This config file is meant for settings that affect your whole blog, values +# which you are expected to set up once and rarely edit after that. If you find +# yourself editing this file very often, consider using Jekyll's data files +# feature for the data you need to update frequently. +# +# For technical reasons, this file is *NOT* reloaded automatically when you use +# 'bundle exec jekyll serve'. If you change this file, please restart the server process. +# +# If you need help with YAML syntax, here are some quick references for you: +# https://learn-the-web.algonquindesign.ca/topics/markdown-yaml-cheat-sheet/#yaml +# https://learnxinyminutes.com/docs/yaml/ +# +# Site settings +# These are used to personalize your new site. If you look in the HTML files, +# you will see them accessed via {{ site.title }}, {{ site.email }}, and so on. +# You can create any custom variable you would like, and they will be accessible +# in the templates via {{ site.myvariable }}. +# +# +# +# +# +# +# + + + +header_pages: + - Introduction.md + - Oceanverse.md + - Faq.md + + + + +markdown: kramdown +title: Coder's High +email: sudarshansudarshan@gmail.com +description: >- # this means to ignore newlines until "baseurl:" + Write an awesome description for your new site here. You can edit this + line in _config.yml. It will appear in your document head meta (for + Google search results) and in your feed.xml site description. +baseurl: /codershigh # the subpath of your site, e.g. /blog +url: https://sudarshansudarshan.github.io # the base hostname & protocol for your site, e.g. http://example.com +twitter_username: jekyllrb +github_username: jekyll + +# Build settings +theme: minima +plugins: + - jekyll-feed + + +# Exclude from processing. +# The following items will not be processed, by default. +# Any item listed under the `exclude:` key here will be automatically added to +# the internal "default list". +# +# Excluded items can be processed by explicitly listing the directories or +# their entries' file path in the `include:` list. +# +# exclude: +# - .sass-cache/ +# - .jekyll-cache/ +# - gemfiles/ +# - Gemfile +# - Gemfile.lock +# - node_modules/ +# - vendor/bundle/ +# - vendor/cache/ +# - vendor/gems/ +# - vendor/ruby/ diff --git a/_includes/disqus_comments.html b/_includes/disqus_comments.html new file mode 100644 index 0000000..d9400f2 --- /dev/null +++ b/_includes/disqus_comments.html @@ -0,0 +1,20 @@ +{%- if page.comments != false and jekyll.environment == "production" -%} + +
+ + +{%- endif -%} diff --git a/_includes/footer.html b/_includes/footer.html new file mode 100644 index 0000000..db72885 --- /dev/null +++ b/_includes/footer.html @@ -0,0 +1,35 @@ +
+ + +
+ +

{{ site.title | escape }}

+ +
+
+
    +
  • + {%- if site.author -%} + {{ site.author | escape }} + {%- else -%} + {{ site.title | escape }} + {%- endif -%} +
    • + {%- if site.email -%} +
  • {{ site.email }}
    • + {%- endif -%} +
+
+ +
+ {%- include social.html -%} +
+ +
+

{{- site.description | escape -}}

+
+
+ +
+ +
diff --git a/_includes/google-analytics.html b/_includes/google-analytics.html new file mode 100644 index 0000000..e9afb20 --- /dev/null +++ b/_includes/google-analytics.html @@ -0,0 +1,12 @@ + + diff --git a/_includes/head.html b/_includes/head.html new file mode 100644 index 0000000..899e96e --- /dev/null +++ b/_includes/head.html @@ -0,0 +1,11 @@ + + + + + {%- seo -%} + + {%- feed_meta -%} + {%- if jekyll.environment == 'production' and site.google_analytics -%} + {%- include google-analytics.html -%} + {%- endif -%} + diff --git a/_includes/header.html b/_includes/header.html new file mode 100644 index 0000000..658531d --- /dev/null +++ b/_includes/header.html @@ -0,0 +1,30 @@ + diff --git a/_includes/icon-github.html b/_includes/icon-github.html new file mode 100644 index 0000000..e501a16 --- /dev/null +++ b/_includes/icon-github.html @@ -0,0 +1 @@ +{% include icon-github.svg %}{{ include.username }} diff --git a/_includes/icon-github.svg b/_includes/icon-github.svg new file mode 100644 index 0000000..e6c5f6d --- /dev/null +++ b/_includes/icon-github.svg @@ -0,0 +1 @@ + diff --git a/_includes/icon-twitter.html b/_includes/icon-twitter.html new file mode 100644 index 0000000..e623dbd --- /dev/null +++ b/_includes/icon-twitter.html @@ -0,0 +1 @@ +{{ include.username }} diff --git a/_includes/icon-twitter.svg b/_includes/icon-twitter.svg new file mode 100644 index 0000000..efc0ecf --- /dev/null +++ b/_includes/icon-twitter.svg @@ -0,0 +1 @@ + diff --git a/_includes/social.html b/_includes/social.html new file mode 100644 index 0000000..44046b8 --- /dev/null +++ b/_includes/social.html @@ -0,0 +1,14 @@ + diff --git a/_layouts/3 b/_layouts/3 new file mode 100644 index 0000000..01c61ed --- /dev/null +++ b/_layouts/3 @@ -0,0 +1,21 @@ + + + {%- include head.html -%} + + + {%- include header.html -%} +
+
+ {{ content }} +
+
+ + + + + + + + + + diff --git a/_layouts/default.html b/_layouts/default.html new file mode 100644 index 0000000..9a5d6aa --- /dev/null +++ b/_layouts/default.html @@ -0,0 +1,21 @@ + + + {%- include head.html -%} + + + {%- include header.html -%} +
+
+ {{ content }} +
+
+ + + + + + + + + + diff --git a/_layouts/home.html b/_layouts/home.html new file mode 100644 index 0000000..7354d99 --- /dev/null +++ b/_layouts/home.html @@ -0,0 +1,39 @@ +--- +layout: default +--- +
+ {%- if page.title -%} +

{{ page.title }}

+ {%- endif -%} + + {{ content }} + +{% comment %} + + {%- if site.posts.size > 0 -%} +

{{ page.list_title | default: "Posts" }}

+
    + {%- for post in site.posts -%} +
  • + {%- assign date_format = site.minima.date_format | default: "%b %-d, %Y" -%} + {{ post.date | date: date_format }} +

    + + {{ post.title | escape }} + +

    + {%- if site.show_excerpts -%} + {{ post.excerpt }} + {%- endif -%} +
    • + {%- endfor -%} +
+ + + + {%- endif -%} + +{% endcomment %} + + +
diff --git a/_layouts/page.html b/_layouts/page.html new file mode 100644 index 0000000..01e4b2a --- /dev/null +++ b/_layouts/page.html @@ -0,0 +1,14 @@ +--- +layout: default +--- +
+ +
+

{{ page.title | escape }}

+
+ +
+ {{ content }} +
+ +
diff --git a/_layouts/post.html b/_layouts/post.html new file mode 100644 index 0000000..abf9696 --- /dev/null +++ b/_layouts/post.html @@ -0,0 +1,27 @@ +--- +layout: default +--- +
+ +
+

{{ page.title | escape }}

+

+ + {%- if page.author -%} + • + {%- endif -%}

+
+ +
+ {{ content }} +
+ + {%- if site.disqus.shortname -%} + {%- include disqus_comments.html -%} + {%- endif -%} + + +
diff --git a/_posts/2022-08-28-test.md b/_posts/2022-08-28-test.md new file mode 100644 index 0000000..9101bc0 --- /dev/null +++ b/_posts/2022-08-28-test.md @@ -0,0 +1,32 @@ +--- +layout: post +title: "Welcome to Jekyll!" +date: 2022-08-28 04:35:00 +0530 +categories: jekyll update +permalink: /two_post +--- +You’ll find this post in your `_posts` directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run `jekyll serve`, which launches a web server and auto-regenerates your site when a file is updated. + +Jekyll requires blog post files to be named according to the following format: + +`YEAR-MONTH-DAY-title.MARKUP` + +Where `YEAR` is a four-digit number, `MONTH` and `DAY` are both two-digit numbers, and `MARKUP` is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works. + +Jekyll also offers powerful support for code snippets: + +{% highlight ruby %} +def print_hi(name) + puts "Hi, #{name}" +end +print_hi('Tom') +#=> prints 'Hi, Tom' to STDOUT. +{% endhighlight %} + +Check out the [Jekyll docs][jekyll-docs] for more info on how to get the most out of Jekyll. File all bugs/feature requests at [Jekyll’s GitHub repo][jekyll-gh]. If you have questions, you can ask them on [Jekyll Talk][jekyll-talk]. + +[jekyll-docs]: https://jekyllrb.com/docs/home +[jekyll-gh]: https://github.com/jekyll/jekyll +[jekyll-talk]: https://talk.jekyllrb.com/ + +All is well diff --git a/_posts/2022-08-28-welcome-to-jekyll.markdown b/_posts/2022-08-28-welcome-to-jekyll.markdown new file mode 100644 index 0000000..38ea30d --- /dev/null +++ b/_posts/2022-08-28-welcome-to-jekyll.markdown @@ -0,0 +1,32 @@ +--- +layout: post +title: "Welcome to Jekyll!" +date: 2022-08-28 04:35:00 +0530 +categories: jekyll update +permalink: /one_post +--- +You’ll find this post in your `_posts` directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run `jekyll serve`, which launches a web server and auto-regenerates your site when a file is updated. + +Jekyll requires blog post files to be named according to the following format: + +`YEAR-MONTH-DAY-title.MARKUP` + +Where `YEAR` is a four-digit number, `MONTH` and `DAY` are both two-digit numbers, and `MARKUP` is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works. + +Jekyll also offers powerful support for code snippets: + +{% highlight ruby %} +def print_hi(name) + puts "Hi, #{name}" +end +print_hi('Tom') +#=> prints 'Hi, Tom' to STDOUT. +{% endhighlight %} + +Check out the [Jekyll docs][jekyll-docs] for more info on how to get the most out of Jekyll. File all bugs/feature requests at [Jekyll’s GitHub repo][jekyll-gh]. If you have questions, you can ask them on [Jekyll Talk][jekyll-talk]. + +[jekyll-docs]: https://jekyllrb.com/docs/home +[jekyll-gh]: https://github.com/jekyll/jekyll +[jekyll-talk]: https://talk.jekyllrb.com/ + +All is well diff --git a/_posts/2022-08-31-My-first-post.md b/_posts/2022-08-31-My-first-post.md new file mode 100644 index 0000000..a4970f5 --- /dev/null +++ b/_posts/2022-08-31-My-first-post.md @@ -0,0 +1,11 @@ +--- +layout: post +title: "Welcome to Jekyll!" +date: 2022-08-28 04:35:00 +0530 +categories: jekyll update +permalink: /new_post/ +--- +This is my first post and I am clueless what to write. It is so nice to preach and not practice what you preach. +Isn't this something that I should contemplate upon? + +Either don't preach, or practice what you preach :-) diff --git a/_sass/minima.scss b/_sass/minima.scss new file mode 100644 index 0000000..cb0865b --- /dev/null +++ b/_sass/minima.scss @@ -0,0 +1,51 @@ +@charset "utf-8"; + +// Define defaults for each variable. + +$base-font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Helvetica, Arial, sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol" !default; +$base-font-size: 16px !default; +$base-font-weight: 400 !default; +$small-font-size: $base-font-size * 0.875 !default; +$base-line-height: 1.5 !default; + +$spacing-unit: 30px !default; + +$text-color: #111 !default; +$background-color: #fdfdfd !default; +$brand-color: #2a7ae2 !default; + +$grey-color: #828282 !default; +$grey-color-light: lighten($grey-color, 40%) !default; +$grey-color-dark: darken($grey-color, 25%) !default; + +$table-text-align: left !default; + +// Width of the content area +$content-width: 800px !default; + +$on-palm: 600px !default; +$on-laptop: 800px !default; + +// Use media queries like this: +// @include media-query($on-palm) { +// .wrapper { +// padding-right: $spacing-unit / 2; +// padding-left: $spacing-unit / 2; +// } +// } +@mixin media-query($device) { + @media screen and (max-width: $device) { + @content; + } +} + +@mixin relative-font-size($ratio) { + font-size: $base-font-size * $ratio; +} + +// Import partials. +@import + "minima/base", + "minima/layout", + "minima/syntax-highlighting" +; diff --git a/_sass/minima/_base.scss b/_sass/minima/_base.scss new file mode 100644 index 0000000..e61b0be --- /dev/null +++ b/_sass/minima/_base.scss @@ -0,0 +1,254 @@ +/** + * Reset some basic elements + */ +body, h1, h2, h3, h4, h5, h6, +p, blockquote, pre, hr, +dl, dd, ol, ul, figure { + margin: 0; + padding: 0; +} + + + +/** + * Basic styling + */ +body { + font: $base-font-weight #{$base-font-size}/#{$base-line-height} $base-font-family; + color: $text-color; + background-color: $background-color; + -webkit-text-size-adjust: 100%; + -webkit-font-feature-settings: "kern" 1; + -moz-font-feature-settings: "kern" 1; + -o-font-feature-settings: "kern" 1; + font-feature-settings: "kern" 1; + font-kerning: normal; + display: flex; + min-height: 100vh; + flex-direction: column; +} + + + +/** + * Set `margin-bottom` to maintain vertical rhythm + */ +h1, h2, h3, h4, h5, h6, +p, blockquote, pre, +ul, ol, dl, figure, +%vertical-rhythm { + margin-bottom: $spacing-unit / 2; +} + + + +/** + * `main` element + */ +main { + display: block; /* Default value of `display` of `main` element is 'inline' in IE 11. */ +} + + + +/** + * Images + */ +img { + max-width: 100%; + vertical-align: middle; +} + + + +/** + * Figures + */ +figure > img { + display: block; +} + +figcaption { + font-size: $small-font-size; +} + + + +/** + * Lists + */ +ul, ol { + margin-left: $spacing-unit; +} + +li { + > ul, + > ol { + margin-bottom: 0; + } +} + + + +/** + * Headings + */ +h1, h2, h3, h4, h5, h6 { + font-weight: $base-font-weight; +} + + + +/** + * Links + */ +a { + color: $brand-color; + text-decoration: none; + + &:visited { + color: darken($brand-color, 15%); + } + + &:hover { + color: $text-color; + text-decoration: underline; + } + + .social-media-list &:hover { + text-decoration: none; + + .username { + text-decoration: underline; + } + } +} + + +/** + * Blockquotes + */ +blockquote { + color: $grey-color; + border-left: 4px solid $grey-color-light; + padding-left: $spacing-unit / 2; + @include relative-font-size(1.125); + letter-spacing: -1px; + font-style: italic; + + > :last-child { + margin-bottom: 0; + } +} + + + +/** + * Code formatting + */ +pre, +code { + @include relative-font-size(0.9375); + border: 1px solid $grey-color-light; + border-radius: 3px; + background-color: #eef; +} + +code { + padding: 1px 5px; +} + +pre { + padding: 8px 12px; + overflow-x: auto; + + > code { + border: 0; + padding-right: 0; + padding-left: 0; + } +} + + + +/** + * Wrapper + */ +.wrapper { + max-width: -webkit-calc(#{$content-width} - (#{$spacing-unit} * 2)); + max-width: calc(#{$content-width} - (#{$spacing-unit} * 2)); + margin-right: auto; + margin-left: auto; + padding-right: $spacing-unit; + padding-left: $spacing-unit; + @extend %clearfix; + + @include media-query($on-laptop) { + max-width: -webkit-calc(#{$content-width} - (#{$spacing-unit})); + max-width: calc(#{$content-width} - (#{$spacing-unit})); + padding-right: $spacing-unit / 2; + padding-left: $spacing-unit / 2; + } +} + + + +/** + * Clearfix + */ +%clearfix:after { + content: ""; + display: table; + clear: both; +} + + + +/** + * Icons + */ + +.svg-icon { + width: 16px; + height: 16px; + display: inline-block; + fill: #{$grey-color}; + padding-right: 5px; + vertical-align: text-top; +} + +.social-media-list { + li + li { + padding-top: 5px; + } +} + + + +/** + * Tables + */ +table { + margin-bottom: $spacing-unit; + width: 100%; + text-align: $table-text-align; + color: lighten($text-color, 18%); + border-collapse: collapse; + border: 1px solid $grey-color-light; + tr { + &:nth-child(even) { + background-color: lighten($grey-color-light, 6%); + } + } + th, td { + padding: ($spacing-unit / 3) ($spacing-unit / 2); + } + th { + background-color: lighten($grey-color-light, 3%); + border: 1px solid darken($grey-color-light, 4%); + border-bottom-color: darken($grey-color-light, 12%); + } + td { + border: 1px solid $grey-color-light; + } +} diff --git a/_sass/minima/_layout.scss b/_sass/minima/_layout.scss new file mode 100644 index 0000000..c69af11 --- /dev/null +++ b/_sass/minima/_layout.scss @@ -0,0 +1,255 @@ +/** + * Site header + */ +.site-header { + border-top: 5px solid $grey-color-dark; + border-bottom: 1px solid $grey-color-light; + min-height: $spacing-unit * 1.865; + + // Positioning context for the mobile navigation icon + position: relative; +} + +.site-title { + @include relative-font-size(1.625); + font-weight: 300; + line-height: $base-line-height * $base-font-size * 2.25; + letter-spacing: -1px; + margin-bottom: 0; + float: left; + + &, + &:visited { + color: $grey-color-dark; + } +} + +.site-nav { + float: right; + line-height: $base-line-height * $base-font-size * 2.25; + + .nav-trigger { + display: none; + } + + .menu-icon { + display: none; + } + + .page-link { + color: $text-color; + line-height: $base-line-height; + + // Gaps between nav items, but not on the last one + &:not(:last-child) { + margin-right: 20px; + } + } + + @include media-query($on-palm) { + position: absolute; + top: 9px; + right: $spacing-unit / 2; + background-color: $background-color; + border: 1px solid $grey-color-light; + border-radius: 5px; + text-align: right; + + label[for="nav-trigger"] { + display: block; + float: right; + width: 36px; + height: 36px; + z-index: 2; + cursor: pointer; + } + + .menu-icon { + display: block; + float: right; + width: 36px; + height: 26px; + line-height: 0; + padding-top: 10px; + text-align: center; + + > svg { + fill: $grey-color-dark; + } + } + + input ~ .trigger { + clear: both; + display: none; + } + + input:checked ~ .trigger { + display: block; + padding-bottom: 5px; + } + + .page-link { + display: block; + padding: 5px 10px; + + &:not(:last-child) { + margin-right: 0; + } + margin-left: 20px; + } + } +} + + + +/** + * Site footer + */ +.site-footer { + border-top: 1px solid $grey-color-light; + padding: $spacing-unit 0; +} + +.footer-heading { + @include relative-font-size(1.125); + margin-bottom: $spacing-unit / 2; +} + +.contact-list, +.social-media-list { + list-style: none; + margin-left: 0; +} + +.footer-col-wrapper { + @include relative-font-size(0.9375); + color: $grey-color; + margin-left: -$spacing-unit / 2; + @extend %clearfix; +} + +.footer-col { + float: left; + margin-bottom: $spacing-unit / 2; + padding-left: $spacing-unit / 2; +} + +.footer-col-1 { + width: -webkit-calc(35% - (#{$spacing-unit} / 2)); + width: calc(35% - (#{$spacing-unit} / 2)); +} + +.footer-col-2 { + width: -webkit-calc(20% - (#{$spacing-unit} / 2)); + width: calc(20% - (#{$spacing-unit} / 2)); +} + +.footer-col-3 { + width: -webkit-calc(45% - (#{$spacing-unit} / 2)); + width: calc(45% - (#{$spacing-unit} / 2)); +} + +@include media-query($on-laptop) { + .footer-col-1, + .footer-col-2 { + width: -webkit-calc(50% - (#{$spacing-unit} / 2)); + width: calc(50% - (#{$spacing-unit} / 2)); + } + + .footer-col-3 { + width: -webkit-calc(100% - (#{$spacing-unit} / 2)); + width: calc(100% - (#{$spacing-unit} / 2)); + } +} + +@include media-query($on-palm) { + .footer-col { + float: none; + width: -webkit-calc(100% - (#{$spacing-unit} / 2)); + width: calc(100% - (#{$spacing-unit} / 2)); + } +} + + + +/** + * Page content + */ +.page-content { + padding: $spacing-unit 0; + flex: 1; +} + +.page-heading { + @include relative-font-size(2); +} + +.post-list-heading { + @include relative-font-size(1.75); +} + +.post-list { + margin-left: 0; + list-style: none; + + > li { + margin-bottom: $spacing-unit; + } +} + +.post-meta { + font-size: $small-font-size; + color: $grey-color; +} + +.post-link { + display: block; + @include relative-font-size(1.5); +} + + + +/** + * Posts + */ +.post-header { + margin-bottom: $spacing-unit; +} + +.post-title { + @include relative-font-size(2.625); + letter-spacing: -1px; + line-height: 1; + + @include media-query($on-laptop) { + @include relative-font-size(2.25); + } +} + +.post-content { + margin-bottom: $spacing-unit; + + h2 { + @include relative-font-size(2); + + @include media-query($on-laptop) { + @include relative-font-size(1.75); + } + } + + h3 { + @include relative-font-size(1.625); + + @include media-query($on-laptop) { + @include relative-font-size(1.375); + } + } + + h4 { + @include relative-font-size(1.25); + + @include media-query($on-laptop) { + @include relative-font-size(1.125); + } + } +} diff --git a/_sass/minima/_syntax-highlighting.scss b/_sass/minima/_syntax-highlighting.scss new file mode 100644 index 0000000..bccdb89 --- /dev/null +++ b/_sass/minima/_syntax-highlighting.scss @@ -0,0 +1,71 @@ +/** + * Syntax highlighting styles + */ +.highlight { + background: #fff; + @extend %vertical-rhythm; + + .highlighter-rouge & { + background: #eef; + } + + .c { color: #998; font-style: italic } // Comment + .err { color: #a61717; background-color: #e3d2d2 } // Error + .k { font-weight: bold } // Keyword + .o { font-weight: bold } // Operator + .cm { color: #998; font-style: italic } // Comment.Multiline + .cp { color: #999; font-weight: bold } // Comment.Preproc + .c1 { color: #998; font-style: italic } // Comment.Single + .cs { color: #999; font-weight: bold; font-style: italic } // Comment.Special + .gd { color: #000; background-color: #fdd } // Generic.Deleted + .gd .x { color: #000; background-color: #faa } // Generic.Deleted.Specific + .ge { font-style: italic } // Generic.Emph + .gr { color: #a00 } // Generic.Error + .gh { color: #999 } // Generic.Heading + .gi { color: #000; background-color: #dfd } // Generic.Inserted + .gi .x { color: #000; background-color: #afa } // Generic.Inserted.Specific + .go { color: #888 } // Generic.Output + .gp { color: #555 } // Generic.Prompt + .gs { font-weight: bold } // Generic.Strong + .gu { color: #aaa } // Generic.Subheading + .gt { color: #a00 } // Generic.Traceback + .kc { font-weight: bold } // Keyword.Constant + .kd { font-weight: bold } // Keyword.Declaration + .kp { font-weight: bold } // Keyword.Pseudo + .kr { font-weight: bold } // Keyword.Reserved + .kt { color: #458; font-weight: bold } // Keyword.Type + .m { color: #099 } // Literal.Number + .s { color: #d14 } // Literal.String + .na { color: #008080 } // Name.Attribute + .nb { color: #0086B3 } // Name.Builtin + .nc { color: #458; font-weight: bold } // Name.Class + .no { color: #008080 } // Name.Constant + .ni { color: #800080 } // Name.Entity + .ne { color: #900; font-weight: bold } // Name.Exception + .nf { color: #900; font-weight: bold } // Name.Function + .nn { color: #555 } // Name.Namespace + .nt { color: #000080 } // Name.Tag + .nv { color: #008080 } // Name.Variable + .ow { font-weight: bold } // Operator.Word + .w { color: #bbb } // Text.Whitespace + .mf { color: #099 } // Literal.Number.Float + .mh { color: #099 } // Literal.Number.Hex + .mi { color: #099 } // Literal.Number.Integer + .mo { color: #099 } // Literal.Number.Oct + .sb { color: #d14 } // Literal.String.Backtick + .sc { color: #d14 } // Literal.String.Char + .sd { color: #d14 } // Literal.String.Doc + .s2 { color: #d14 } // Literal.String.Double + .se { color: #d14 } // Literal.String.Escape + .sh { color: #d14 } // Literal.String.Heredoc + .si { color: #d14 } // Literal.String.Interpol + .sx { color: #d14 } // Literal.String.Other + .sr { color: #009926 } // Literal.String.Regex + .s1 { color: #d14 } // Literal.String.Single + .ss { color: #990073 } // Literal.String.Symbol + .bp { color: #999 } // Name.Builtin.Pseudo + .vc { color: #008080 } // Name.Variable.Class + .vg { color: #008080 } // Name.Variable.Global + .vi { color: #008080 } // Name.Variable.Instance + .il { color: #099 } // Literal.Number.Integer.Long +} diff --git a/_site/404.html b/_site/404.html new file mode 100644 index 0000000..c90a3ca --- /dev/null +++ b/_site/404.html @@ -0,0 +1,95 @@ + + + + + +Coder’s High | Write an awesome description for your new site here. You can edit this line in _config.yml. It will appear in your document head meta (for Google search results) and in your feed.xml site description. + + + + + + + + + + + + + + + +
+
+ + +
+

404

+ +

Page not found :(

+

The requested page could not be found.

+
+ +
+
+ + + + + + + + + + diff --git a/_site/LICENSE.txt b/_site/LICENSE.txt new file mode 100644 index 0000000..0e7ecd8 --- /dev/null +++ b/_site/LICENSE.txt @@ -0,0 +1,21 @@ +The MIT License (MIT) + +Copyright (c) 2016-present Parker Moore and the minima contributors + +Permission is hereby granted, free of charge, to any person obtaining a copy +of this software and associated documentation files (the "Software"), to deal +in the Software without restriction, including without limitation the rights +to use, copy, modify, merge, publish, distribute, sublicense, and/or sell +copies of the Software, and to permit persons to whom the Software is +furnished to do so, subject to the following conditions: + +The above copyright notice and this permission notice shall be included in +all copies or substantial portions of the Software. + +THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR +IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, +FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE +AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER +LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, +OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN +THE SOFTWARE. diff --git a/_site/README.md b/_site/README.md new file mode 100644 index 0000000..1f5f137 --- /dev/null +++ b/_site/README.md @@ -0,0 +1,220 @@ +# minima + +*Minima is a one-size-fits-all Jekyll theme for writers*. It's Jekyll's default (and first) theme. It's what you get when you run `jekyll new`. + +[Theme preview](https://jekyll.github.io/minima/) + +![minima theme preview](/screenshot.png) + +$$a^2$$ + +## Installation + +Add this line to your Jekyll site's Gemfile: + +```ruby +gem "minima" +``` + +And add this line to your Jekyll site: + +```yaml +theme: minima +``` + +And then execute: + + $ bundle + + +## Contents At-A-Glance + +Minima has been scaffolded by the `jekyll new-theme` command and therefore has all the necessary files and directories to have a new Jekyll site up and running with zero-configuration. + +### Layouts + +Refers to files within the `_layouts` directory, that define the markup for your theme. + + - `default.html` — The base layout that lays the foundation for subsequent layouts. The derived layouts inject their contents into this file at the line that says ` {{ content }} ` and are linked to this file via [FrontMatter](https://jekyllrb.com/docs/frontmatter/) declaration `layout: default`. + - `home.html` — The layout for your landing-page / home-page / index-page. [[More Info.](#home-layout)] + - `page.html` — The layout for your documents that contain FrontMatter, but are not posts. + - `post.html` — The layout for your posts. + +### Includes + +Refers to snippets of code within the `_includes` directory that can be inserted in multiple layouts (and another include-file as well) within the same theme-gem. + + - `disqus_comments.html` — Code to markup disqus comment box. + - `footer.html` — Defines the site's footer section. + - `google-analytics.html` — Inserts Google Analytics module (active only in production environment). + - `head.html` — Code-block that defines the `` in *default* layout. + - `header.html` — Defines the site's main header section. By default, pages with a defined `title` attribute will have links displayed here. + +### Sass + +Refers to `.scss` files within the `_sass` directory that define the theme's styles. + + - `minima.scss` — The core file imported by preprocessed `main.scss`, it defines the variable defaults for the theme and also further imports sass partials to supplement itself. + - `minima/_base.scss` — Resets and defines base styles for various HTML elements. + - `minima/_layout.scss` — Defines the visual style for various layouts. + - `minima/_syntax-highlighting.scss` — Defines the styles for syntax-highlighting. + +### Assets + +Refers to various asset files within the `assets` directory. +Contains the `main.scss` that imports sass files from within the `_sass` directory. This `main.scss` is what gets processed into the theme's main stylesheet `main.css` called by `_layouts/default.html` via `_includes/head.html`. + +This directory can include sub-directories to manage assets of similar type, and will be copied over as is, to the final transformed site directory. + +### Plugins + +Minima comes with [`jekyll-seo-tag`](https://github.com/jekyll/jekyll-seo-tag) plugin preinstalled to make sure your website gets the most useful meta tags. See [usage](https://github.com/jekyll/jekyll-seo-tag#usage) to know how to set it up. + +## Usage + +### Home Layout + +`home.html` is a flexible HTML layout for the site's landing-page / home-page / index-page.
+ +#### Main Heading and Content-injection + +From Minima v2.2 onwards, the *home* layout will inject all content from your `index.md` / `index.html` **before** the **`Posts`** heading. This will allow you to include non-posts related content to be published on the landing page under a dedicated heading. *We recommended that you title this section with a Heading2 (`##`)*. + +Usually the `site.title` itself would suffice as the implicit 'main-title' for a landing-page. But, if your landing-page would like a heading to be explicitly displayed, then simply define a `title` variable in the document's front matter and it will be rendered with an `

` tag. + +#### Post Listing + +This section is optional from Minima v2.2 onwards.
+It will be automatically included only when your site contains one or more valid posts or drafts (if the site is configured to `show_drafts`). + +The title for this section is `Posts` by default and rendered with an `

` tag. You can customize this heading by defining a `list_title` variable in the document's front matter. + +-- + +### Customization + +To override the default structure and style of minima, simply create the concerned directory at the root of your site, copy the file you wish to customize to that directory, and then edit the file. +e.g., to override the [`_includes/head.html `](_includes/head.html) file to specify a custom style path, create an `_includes` directory, copy `_includes/head.html` from minima gem folder to `/_includes` and start editing that file. + +The site's default CSS has now moved to a new place within the gem itself, [`assets/main.scss`](assets/main.scss). To **override the default CSS**, the file has to exist at your site source. Do either of the following: +- Create a new instance of `main.scss` at site source. + - Create a new file `main.scss` at `/assets/` + - Add the frontmatter dashes, and + - Add `@import "minima";`, to `/assets/main.scss` + - Add your custom CSS. +- Download the file from this repo + - Create a new file `main.scss` at `/assets/` + - Copy the contents at [assets/main.scss](assets/main.scss) onto the `main.scss` you just created, and edit away! +- Copy directly from Minima 2.0 gem + - Go to your local minima gem installation directory ( run `bundle show minima` to get the path to it ). + - Copy the `assets/` folder from there into the root of `` + - Change whatever values you want, inside `/assets/main.scss` + +-- + +### Customize navigation links + +This allows you to set which pages you want to appear in the navigation area and configure order of the links. + +For instance, to only link to the `about` and the `portfolio` page, add the following to you `_config.yml`: + +```yaml +header_pages: + - about.md + - portfolio.md +``` + +-- + +### Change default date format + +You can change the default date format by specifying `site.minima.date_format` +in `_config.yml`. + +``` +# Minima date format +# refer to http://shopify.github.io/liquid/filters/date/ if you want to customize this +minima: + date_format: "%b %-d, %Y" +``` + +-- + +### Enabling comments (via Disqus) + +Optionally, if you have a Disqus account, you can tell Jekyll to use it to show a comments section below each post. + +To enable it, add the following lines to your Jekyll site: + +```yaml + disqus: + shortname: my_disqus_shortname +``` + +You can find out more about Disqus' shortnames [here](https://help.disqus.com/customer/portal/articles/466208). + +Comments are enabled by default and will only appear in production, i.e., `JEKYLL_ENV=production` + +If you don't want to display comments for a particular post you can disable them by adding `comments: false` to that post's YAML Front Matter. + +-- + +### Social networks + +You can add links to the accounts you have on other sites, with respective icon, by adding one or more of the following options in your config: + +```yaml +twitter_username: jekyllrb +github_username: jekyll +dribbble_username: jekyll +facebook_username: jekyll +flickr_username: jekyll +instagram_username: jekyll +linkedin_username: jekyll +pinterest_username: jekyll +youtube_username: jekyll +googleplus_username: +jekyll +rss: rss + +mastodon: + - username: jekyll + instance: example.com + - username: jekyll2 + instance: example.com +``` + +-- + +### Enabling Google Analytics + +To enable Google Analytics, add the following lines to your Jekyll site: + +```yaml + google_analytics: UA-NNNNNNNN-N +``` + +Google Analytics will only appear in production, i.e., `JEKYLL_ENV=production` + +-- + +### Enabling Excerpts on the Home Page + +To display post-excerpts on the Home Page, simply add the following to your `_config.yml`: + +```yaml +show_excerpts: true +``` + +## Contributing + +Bug reports and pull requests are welcome on GitHub at https://github.com/jekyll/minima. This project is intended to be a safe, welcoming space for collaboration, and contributors are expected to adhere to the [Contributor Covenant](http://contributor-covenant.org) code of conduct. + +## Development + +To set up your environment to develop this theme, run `script/bootstrap`. + +To test your theme, run `script/server` (or `bundle exec jekyll serve`) and open your browser at `http://localhost:4000`. This starts a Jekyll server using your theme and the contents. As you make modifications, your site will regenerate and you should see the changes in the browser after a refresh. + +## License + +The theme is available as open source under the terms of the [MIT License](http://opensource.org/licenses/MIT). diff --git a/_site/assets/christ.jpg b/_site/assets/christ.jpg new file mode 100644 index 0000000..bb61a7a Binary files /dev/null and b/_site/assets/christ.jpg differ diff --git a/_site/assets/main.css b/_site/assets/main.css new file mode 100644 index 0000000..5ae9716 --- /dev/null +++ b/_site/assets/main.css @@ -0,0 +1,649 @@ +/** + * Reset some basic elements + */ +body, h1, h2, h3, h4, h5, h6, +p, blockquote, pre, hr, +dl, dd, ol, ul, figure { + margin: 0; + padding: 0; +} + +/** + * Basic styling + */ +body { + font: 400 16px/1.5 -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Helvetica, Arial, sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol"; + color: #111; + background-color: #fdfdfd; + -webkit-text-size-adjust: 100%; + -webkit-font-feature-settings: "kern" 1; + -moz-font-feature-settings: "kern" 1; + -o-font-feature-settings: "kern" 1; + font-feature-settings: "kern" 1; + font-kerning: normal; + display: flex; + min-height: 100vh; + flex-direction: column; +} + +/** + * Set `margin-bottom` to maintain vertical rhythm + */ +h1, h2, h3, h4, h5, h6, +p, blockquote, pre, +ul, ol, dl, figure, +.highlight { + margin-bottom: 15px; +} + +/** + * `main` element + */ +main { + display: block; /* Default value of `display` of `main` element is 'inline' in IE 11. */ +} + +/** + * Images + */ +img { + max-width: 100%; + vertical-align: middle; +} + +/** + * Figures + */ +figure > img { + display: block; +} + +figcaption { + font-size: 14px; +} + +/** + * Lists + */ +ul, ol { + margin-left: 30px; +} + +li > ul, +li > ol { + margin-bottom: 0; +} + +/** + * Headings + */ +h1, h2, h3, h4, h5, h6 { + font-weight: 400; +} + +/** + * Links + */ +a { + color: #2a7ae2; + text-decoration: none; +} +a:visited { + color: #1756a9; +} +a:hover { + color: #111; + text-decoration: underline; +} +.social-media-list a:hover { + text-decoration: none; +} +.social-media-list a:hover .username { + text-decoration: underline; +} + +/** + * Blockquotes + */ +blockquote { + color: #828282; + border-left: 4px solid #e8e8e8; + padding-left: 15px; + font-size: 18px; + letter-spacing: -1px; + font-style: italic; +} +blockquote > :last-child { + margin-bottom: 0; +} + +/** + * Code formatting + */ +pre, +code { + font-size: 15px; + border: 1px solid #e8e8e8; + border-radius: 3px; + background-color: #eef; +} + +code { + padding: 1px 5px; +} + +pre { + padding: 8px 12px; + overflow-x: auto; +} +pre > code { + border: 0; + padding-right: 0; + padding-left: 0; +} + +/** + * Wrapper + */ +.wrapper { + max-width: -webkit-calc(800px - (30px * 2)); + max-width: calc(800px - 30px * 2); + margin-right: auto; + margin-left: auto; + padding-right: 30px; + padding-left: 30px; +} +@media screen and (max-width: 800px) { + .wrapper { + max-width: -webkit-calc(800px - (30px)); + max-width: calc(800px - (30px)); + padding-right: 15px; + padding-left: 15px; + } +} + +/** + * Clearfix + */ +.footer-col-wrapper:after, .wrapper:after { + content: ""; + display: table; + clear: both; +} + +/** + * Icons + */ +.svg-icon { + width: 16px; + height: 16px; + display: inline-block; + fill: #828282; + padding-right: 5px; + vertical-align: text-top; +} + +.social-media-list li + li { + padding-top: 5px; +} + +/** + * Tables + */ +table { + margin-bottom: 30px; + width: 100%; + text-align: left; + color: #3f3f3f; + border-collapse: collapse; + border: 1px solid #e8e8e8; +} +table tr:nth-child(even) { + background-color: #f7f7f7; +} +table th, table td { + padding: 10px 15px; +} +table th { + background-color: #f0f0f0; + border: 1px solid #dedede; + border-bottom-color: #c9c9c9; +} +table td { + border: 1px solid #e8e8e8; +} + +/** + * Site header + */ +.site-header { + border-top: 5px solid #424242; + border-bottom: 1px solid #e8e8e8; + min-height: 55.95px; + position: relative; +} + +.site-title { + font-size: 26px; + font-weight: 300; + line-height: 54px; + letter-spacing: -1px; + margin-bottom: 0; + float: left; +} +.site-title, .site-title:visited { + color: #424242; +} + +.site-nav { + float: right; + line-height: 54px; +} +.site-nav .nav-trigger { + display: none; +} +.site-nav .menu-icon { + display: none; +} +.site-nav .page-link { + color: #111; + line-height: 1.5; +} +.site-nav .page-link:not(:last-child) { + margin-right: 20px; +} +@media screen and (max-width: 600px) { + .site-nav { + position: absolute; + top: 9px; + right: 15px; + background-color: #fdfdfd; + border: 1px solid #e8e8e8; + border-radius: 5px; + text-align: right; + } + .site-nav label[for=nav-trigger] { + display: block; + float: right; + width: 36px; + height: 36px; + z-index: 2; + cursor: pointer; + } + .site-nav .menu-icon { + display: block; + float: right; + width: 36px; + height: 26px; + line-height: 0; + padding-top: 10px; + text-align: center; + } + .site-nav .menu-icon > svg { + fill: #424242; + } + .site-nav input ~ .trigger { + clear: both; + display: none; + } + .site-nav input:checked ~ .trigger { + display: block; + padding-bottom: 5px; + } + .site-nav .page-link { + display: block; + padding: 5px 10px; + margin-left: 20px; + } + .site-nav .page-link:not(:last-child) { + margin-right: 0; + } +} + +/** + * Site footer + */ +.site-footer { + border-top: 1px solid #e8e8e8; + padding: 30px 0; +} + +.footer-heading { + font-size: 18px; + margin-bottom: 15px; +} + +.contact-list, +.social-media-list { + list-style: none; + margin-left: 0; +} + +.footer-col-wrapper { + font-size: 15px; + color: #828282; + margin-left: -15px; +} + +.footer-col { + float: left; + margin-bottom: 15px; + padding-left: 15px; +} + +.footer-col-1 { + width: -webkit-calc(35% - (30px / 2)); + width: calc(35% - 30px / 2); +} + +.footer-col-2 { + width: -webkit-calc(20% - (30px / 2)); + width: calc(20% - 30px / 2); +} + +.footer-col-3 { + width: -webkit-calc(45% - (30px / 2)); + width: calc(45% - 30px / 2); +} + +@media screen and (max-width: 800px) { + .footer-col-1, + .footer-col-2 { + width: -webkit-calc(50% - (30px / 2)); + width: calc(50% - 30px / 2); + } + .footer-col-3 { + width: -webkit-calc(100% - (30px / 2)); + width: calc(100% - 30px / 2); + } +} +@media screen and (max-width: 600px) { + .footer-col { + float: none; + width: -webkit-calc(100% - (30px / 2)); + width: calc(100% - 30px / 2); + } +} +/** + * Page content + */ +.page-content { + padding: 30px 0; + flex: 1; +} + +.page-heading { + font-size: 32px; +} + +.post-list-heading { + font-size: 28px; +} + +.post-list { + margin-left: 0; + list-style: none; +} +.post-list > li { + margin-bottom: 30px; +} + +.post-meta { + font-size: 14px; + color: #828282; +} + +.post-link { + display: block; + font-size: 24px; +} + +/** + * Posts + */ +.post-header { + margin-bottom: 30px; +} + +.post-title { + font-size: 42px; + letter-spacing: -1px; + line-height: 1; +} +@media screen and (max-width: 800px) { + .post-title { + font-size: 36px; + } +} + +.post-content { + margin-bottom: 30px; +} +.post-content h2 { + font-size: 32px; +} +@media screen and (max-width: 800px) { + .post-content h2 { + font-size: 28px; + } +} +.post-content h3 { + font-size: 26px; +} +@media screen and (max-width: 800px) { + .post-content h3 { + font-size: 22px; + } +} +.post-content h4 { + font-size: 20px; +} +@media screen and (max-width: 800px) { + .post-content h4 { + font-size: 18px; + } +} + +/** + * Syntax highlighting styles + */ +.highlight { + background: #fff; +} +.highlighter-rouge .highlight { + background: #eef; +} +.highlight .c { + color: #998; + font-style: italic; +} +.highlight .err { + color: #a61717; + background-color: #e3d2d2; +} +.highlight .k { + font-weight: bold; +} +.highlight .o { + font-weight: bold; +} +.highlight .cm { + color: #998; + font-style: italic; +} +.highlight .cp { + color: #999; + font-weight: bold; +} +.highlight .c1 { + color: #998; + font-style: italic; +} +.highlight .cs { + color: #999; + font-weight: bold; + font-style: italic; +} +.highlight .gd { + color: #000; + background-color: #fdd; +} +.highlight .gd .x { + color: #000; + background-color: #faa; +} +.highlight .ge { + font-style: italic; +} +.highlight .gr { + color: #a00; +} +.highlight .gh { + color: #999; +} +.highlight .gi { + color: #000; + background-color: #dfd; +} +.highlight .gi .x { + color: #000; + background-color: #afa; +} +.highlight .go { + color: #888; +} +.highlight .gp { + color: #555; +} +.highlight .gs { + font-weight: bold; +} +.highlight .gu { + color: #aaa; +} +.highlight .gt { + color: #a00; +} +.highlight .kc { + font-weight: bold; +} +.highlight .kd { + font-weight: bold; +} +.highlight .kp { + font-weight: bold; +} +.highlight .kr { + font-weight: bold; +} +.highlight .kt { + color: #458; + font-weight: bold; +} +.highlight .m { + color: #099; +} +.highlight .s { + color: #d14; +} +.highlight .na { + color: #008080; +} +.highlight .nb { + color: #0086B3; +} +.highlight .nc { + color: #458; + font-weight: bold; +} +.highlight .no { + color: #008080; +} +.highlight .ni { + color: #800080; +} +.highlight .ne { + color: #900; + font-weight: bold; +} +.highlight .nf { + color: #900; + font-weight: bold; +} +.highlight .nn { + color: #555; +} +.highlight .nt { + color: #000080; +} +.highlight .nv { + color: #008080; +} +.highlight .ow { + font-weight: bold; +} +.highlight .w { + color: #bbb; +} +.highlight .mf { + color: #099; +} +.highlight .mh { + color: #099; +} +.highlight .mi { + color: #099; +} +.highlight .mo { + color: #099; +} +.highlight .sb { + color: #d14; +} +.highlight .sc { + color: #d14; +} +.highlight .sd { + color: #d14; +} +.highlight .s2 { + color: #d14; +} +.highlight .se { + color: #d14; +} +.highlight .sh { + color: #d14; +} +.highlight .si { + color: #d14; +} +.highlight .sx { + color: #d14; +} +.highlight .sr { + color: #009926; +} +.highlight .s1 { + color: #d14; +} +.highlight .ss { + color: #990073; +} +.highlight .bp { + color: #999; +} +.highlight .vc { + color: #008080; +} +.highlight .vg { + color: #008080; +} +.highlight .vi { + color: #008080; +} +.highlight .il { + color: #099; +} + +/*# sourceMappingURL=main.css.map */ \ No newline at end of file diff --git a/_site/assets/main.css.map b/_site/assets/main.css.map new file mode 100644 index 0000000..f6745ec --- /dev/null +++ b/_site/assets/main.css.map @@ -0,0 +1 @@ +{"version":3,"sourceRoot":"","sources":["../_sass/minima/_base.scss","../_sass/minima.scss","../_sass/minima/_layout.scss","../_sass/minima/_syntax-highlighting.scss"],"names":[],"mappings":"AAAA;AAAA;AAAA;AAGA;AAAA;AAAA;EAGE;EACA;;;AAKF;AAAA;AAAA;AAGA;EACE;EACA,OCLiB;EDMjB,kBCLiB;EDMjB;EACA;EACG;EACE;EACG;EACR;EACA;EACA;EACA;;;AAKF;AAAA;AAAA;AAGA;AAAA;AAAA;AAAA;EAIE;;;AAKF;AAAA;AAAA;AAGA;EACE;;;AAKF;AAAA;AAAA;AAGA;EACE;EACA;;;AAKF;AAAA;AAAA;AAGA;EACE;;;AAGF;EACE,WChEiB;;;ADqEnB;AAAA;AAAA;AAGA;EACE,aCtEiB;;;AD0EjB;AAAA;EAEE;;;AAMJ;AAAA;AAAA;AAGA;EACE,aC1FiB;;;AD+FnB;AAAA;AAAA;AAGA;EACE,OC3FiB;ED4FjB;;AAEA;EACE;;AAGF;EACE,OCrGe;EDsGf;;AAGF;EACE;;AAEA;EACE;;;AAMN;AAAA;AAAA;AAGA;EACE,OCnHiB;EDoHjB;EACA;EC3FA;ED6FA;EACA;;AAEA;EACE;;;AAMJ;AAAA;AAAA;AAGA;AAAA;EC1GE;ED6GA;EACA;EACA;;;AAGF;EACE;;;AAGF;EACE;EACA;;AAEA;EACE;EACA;EACA;;;AAMJ;AAAA;AAAA;AAGA;EACE;EACA;EACA;EACA;EACA,eC3KiB;ED4KjB,cC5KiB;;AA0BjB;ED4IF;IAUI;IACA;IACA;IACA;;;;AAMJ;AAAA;AAAA;AAGA;EACE;EACA;EACA;;;AAKF;AAAA;AAAA;AAIA;EACI;EACA;EACA;EACA;EACA;EACA;;;AAIF;EACE;;;AAMJ;AAAA;AAAA;AAGA;EACE,eC7NiB;ED8NjB;EACA,YCrNiB;EDsNjB;EACA;EACA;;AAEE;EACE;;AAGJ;EACE;;AAEF;EACE;EACA;EACA;;AAEF;EACE;;;AE3PJ;AAAA;AAAA;AAGA;EACE;EACA;EACA;EAGA;;;AAGF;ED8BE;EC5BA;EACA;EACA;EACA;EACA;;AAEA;EAEE,ODJe;;;ACQnB;EACE;EACA;;AAEA;EACI;;AAGJ;EACE;;AAGF;EACE,OD3Be;EC4Bf,aDhCe;;ACmCf;EACE;;ADRJ;ECVF;IAuBI;IACA;IACA;IACA,kBDvCe;ICwCf;IACA;IACA;;EAEA;IACE;IACA;IACA;IACA;IACA;IACA;;EAGF;IACE;IACA;IACA;IACA;IACA;IACA;IACA;;EAEA;IACE,MD1DW;;EC8Df;IACE;IACA;;EAGF;IACE;IACA;;EAGF;IACE;IACA;IAKA;;EAHA;IACE;;;;AASR;AAAA;AAAA;AAGA;EACE;EACA;;;AAGF;EDtEE;ECwEA;;;AAGF;AAAA;EAEE;EACA;;;AAGF;EDjFE;ECmFA,OD7GiB;EC8GjB;;;AAIF;EACE;EACA;EACA;;;AAGF;EACE;EACA;;;AAGF;EACE;EACA;;;AAGF;EACE;EACA;;;ADhHA;ECoHA;AAAA;IAEE;IACA;;EAGF;IACE;IACA;;;AD5HF;ECiIA;IACE;IACA;IACA;;;AAMJ;AAAA;AAAA;AAGA;EACE;EACA;;;AAGF;ED5IE;;;ACgJF;EDhJE;;;ACoJF;EACE;EACA;;AAEA;EACE,eDzLe;;;AC6LnB;EACE,WDjMiB;ECkMjB,ODzLiB;;;AC4LnB;EACE;EDnKA;;;ACyKF;AAAA;AAAA;AAGA;EACE,eD7MiB;;;ACgNnB;EDhLE;ECkLA;EACA;;ADzLA;ECsLF;IDhLE;;;;AC0LF;EACE,eD3NiB;;AC6NjB;ED7LA;;AANA;ECmMA;ID7LA;;;ACqMA;EDrMA;;AANA;EC2MA;IDrMA;;;AC6MA;ED7MA;;AANA;ECmNA;ID7MA;;;;AE1CF;AAAA;AAAA;AAGA;EACE;;AAGA;EACE;;AAGF;EAAS;EAAa;;AACtB;EAAS;EAAgB;;AACzB;EAAS;;AACT;EAAS;;AACT;EAAS;EAAa;;AACtB;EAAS;EAAa;;AACtB;EAAS;EAAa;;AACtB;EAAS;EAAa;EAAmB;;AACzC;EAAS;EAAa;;AACtB;EAAS;EAAa;;AACtB;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;EAAa;;AACtB;EAAS;EAAa;;AACtB;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;EAAa;;AACtB;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;EAAa;;AACtB;EAAS;;AACT;EAAS;;AACT;EAAS;EAAa;;AACtB;EAAS;EAAa;;AACtB;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS;;AACT;EAAS","sourcesContent":["/**\n * Reset some basic elements\n */\nbody, h1, h2, h3, h4, h5, h6,\np, blockquote, pre, hr,\ndl, dd, ol, ul, figure {\n margin: 0;\n padding: 0;\n}\n\n\n\n/**\n * Basic styling\n */\nbody {\n font: $base-font-weight #{$base-font-size}/#{$base-line-height} $base-font-family;\n color: $text-color;\n background-color: $background-color;\n -webkit-text-size-adjust: 100%;\n -webkit-font-feature-settings: \"kern\" 1;\n -moz-font-feature-settings: \"kern\" 1;\n -o-font-feature-settings: \"kern\" 1;\n font-feature-settings: \"kern\" 1;\n font-kerning: normal;\n display: flex;\n min-height: 100vh;\n flex-direction: column;\n}\n\n\n\n/**\n * Set `margin-bottom` to maintain vertical rhythm\n */\nh1, h2, h3, h4, h5, h6,\np, blockquote, pre,\nul, ol, dl, figure,\n%vertical-rhythm {\n margin-bottom: $spacing-unit / 2;\n}\n\n\n\n/**\n * `main` element\n */\nmain {\n display: block; /* Default value of `display` of `main` element is 'inline' in IE 11. */\n}\n\n\n\n/**\n * Images\n */\nimg {\n max-width: 100%;\n vertical-align: middle;\n}\n\n\n\n/**\n * Figures\n */\nfigure > img {\n display: block;\n}\n\nfigcaption {\n font-size: $small-font-size;\n}\n\n\n\n/**\n * Lists\n */\nul, ol {\n margin-left: $spacing-unit;\n}\n\nli {\n > ul,\n > ol {\n margin-bottom: 0;\n }\n}\n\n\n\n/**\n * Headings\n */\nh1, h2, h3, h4, h5, h6 {\n font-weight: $base-font-weight;\n}\n\n\n\n/**\n * Links\n */\na {\n color: $brand-color;\n text-decoration: none;\n\n &:visited {\n color: darken($brand-color, 15%);\n }\n\n &:hover {\n color: $text-color;\n text-decoration: underline;\n }\n\n .social-media-list &:hover {\n text-decoration: none;\n\n .username {\n text-decoration: underline;\n }\n }\n}\n\n\n/**\n * Blockquotes\n */\nblockquote {\n color: $grey-color;\n border-left: 4px solid $grey-color-light;\n padding-left: $spacing-unit / 2;\n @include relative-font-size(1.125);\n letter-spacing: -1px;\n font-style: italic;\n\n > :last-child {\n margin-bottom: 0;\n }\n}\n\n\n\n/**\n * Code formatting\n */\npre,\ncode {\n @include relative-font-size(0.9375);\n border: 1px solid $grey-color-light;\n border-radius: 3px;\n background-color: #eef;\n}\n\ncode {\n padding: 1px 5px;\n}\n\npre {\n padding: 8px 12px;\n overflow-x: auto;\n\n > code {\n border: 0;\n padding-right: 0;\n padding-left: 0;\n }\n}\n\n\n\n/**\n * Wrapper\n */\n.wrapper {\n max-width: -webkit-calc(#{$content-width} - (#{$spacing-unit} * 2));\n max-width: calc(#{$content-width} - (#{$spacing-unit} * 2));\n margin-right: auto;\n margin-left: auto;\n padding-right: $spacing-unit;\n padding-left: $spacing-unit;\n @extend %clearfix;\n\n @include media-query($on-laptop) {\n max-width: -webkit-calc(#{$content-width} - (#{$spacing-unit}));\n max-width: calc(#{$content-width} - (#{$spacing-unit}));\n padding-right: $spacing-unit / 2;\n padding-left: $spacing-unit / 2;\n }\n}\n\n\n\n/**\n * Clearfix\n */\n%clearfix:after {\n content: \"\";\n display: table;\n clear: both;\n}\n\n\n\n/**\n * Icons\n */\n\n.svg-icon {\n width: 16px;\n height: 16px;\n display: inline-block;\n fill: #{$grey-color};\n padding-right: 5px;\n vertical-align: text-top;\n}\n\n.social-media-list {\n li + li {\n padding-top: 5px;\n }\n}\n\n\n\n/**\n * Tables\n */\ntable {\n margin-bottom: $spacing-unit;\n width: 100%;\n text-align: $table-text-align;\n color: lighten($text-color, 18%);\n border-collapse: collapse;\n border: 1px solid $grey-color-light;\n tr {\n &:nth-child(even) {\n background-color: lighten($grey-color-light, 6%);\n }\n }\n th, td {\n padding: ($spacing-unit / 3) ($spacing-unit / 2);\n }\n th {\n background-color: lighten($grey-color-light, 3%);\n border: 1px solid darken($grey-color-light, 4%);\n border-bottom-color: darken($grey-color-light, 12%);\n }\n td {\n border: 1px solid $grey-color-light;\n }\n}\n","@charset \"utf-8\";\n\n// Define defaults for each variable.\n\n$base-font-family: -apple-system, BlinkMacSystemFont, \"Segoe UI\", Roboto, Helvetica, Arial, sans-serif, \"Apple Color Emoji\", \"Segoe UI Emoji\", \"Segoe UI Symbol\" !default;\n$base-font-size: 16px !default;\n$base-font-weight: 400 !default;\n$small-font-size: $base-font-size * 0.875 !default;\n$base-line-height: 1.5 !default;\n\n$spacing-unit: 30px !default;\n\n$text-color: #111 !default;\n$background-color: #fdfdfd !default;\n$brand-color: #2a7ae2 !default;\n\n$grey-color: #828282 !default;\n$grey-color-light: lighten($grey-color, 40%) !default;\n$grey-color-dark: darken($grey-color, 25%) !default;\n\n$table-text-align: left !default;\n\n// Width of the content area\n$content-width: 800px !default;\n\n$on-palm: 600px !default;\n$on-laptop: 800px !default;\n\n// Use media queries like this:\n// @include media-query($on-palm) {\n// .wrapper {\n// padding-right: $spacing-unit / 2;\n// padding-left: $spacing-unit / 2;\n// }\n// }\n@mixin media-query($device) {\n @media screen and (max-width: $device) {\n @content;\n }\n}\n\n@mixin relative-font-size($ratio) {\n font-size: $base-font-size * $ratio;\n}\n\n// Import partials.\n@import\n \"minima/base\",\n \"minima/layout\",\n \"minima/syntax-highlighting\"\n;\n","/**\n * Site header\n */\n.site-header {\n border-top: 5px solid $grey-color-dark;\n border-bottom: 1px solid $grey-color-light;\n min-height: $spacing-unit * 1.865;\n\n // Positioning context for the mobile navigation icon\n position: relative;\n}\n\n.site-title {\n @include relative-font-size(1.625);\n font-weight: 300;\n line-height: $base-line-height * $base-font-size * 2.25;\n letter-spacing: -1px;\n margin-bottom: 0;\n float: left;\n\n &,\n &:visited {\n color: $grey-color-dark;\n }\n}\n\n.site-nav {\n float: right;\n line-height: $base-line-height * $base-font-size * 2.25;\n\n .nav-trigger {\n display: none;\n }\n\n .menu-icon {\n display: none;\n }\n\n .page-link {\n color: $text-color;\n line-height: $base-line-height;\n\n // Gaps between nav items, but not on the last one\n &:not(:last-child) {\n margin-right: 20px;\n }\n }\n\n @include media-query($on-palm) {\n position: absolute;\n top: 9px;\n right: $spacing-unit / 2;\n background-color: $background-color;\n border: 1px solid $grey-color-light;\n border-radius: 5px;\n text-align: right;\n\n label[for=\"nav-trigger\"] {\n display: block;\n float: right;\n width: 36px;\n height: 36px;\n z-index: 2;\n cursor: pointer;\n }\n\n .menu-icon {\n display: block;\n float: right;\n width: 36px;\n height: 26px;\n line-height: 0;\n padding-top: 10px;\n text-align: center;\n\n > svg {\n fill: $grey-color-dark;\n }\n }\n\n input ~ .trigger {\n clear: both;\n display: none;\n }\n\n input:checked ~ .trigger {\n display: block;\n padding-bottom: 5px;\n }\n\n .page-link {\n display: block;\n padding: 5px 10px;\n\n &:not(:last-child) {\n margin-right: 0;\n }\n margin-left: 20px;\n }\n }\n}\n\n\n\n/**\n * Site footer\n */\n.site-footer {\n border-top: 1px solid $grey-color-light;\n padding: $spacing-unit 0;\n}\n\n.footer-heading {\n @include relative-font-size(1.125);\n margin-bottom: $spacing-unit / 2;\n}\n\n.contact-list,\n.social-media-list {\n list-style: none;\n margin-left: 0;\n}\n\n.footer-col-wrapper {\n @include relative-font-size(0.9375);\n color: $grey-color;\n margin-left: -$spacing-unit / 2;\n @extend %clearfix;\n}\n\n.footer-col {\n float: left;\n margin-bottom: $spacing-unit / 2;\n padding-left: $spacing-unit / 2;\n}\n\n.footer-col-1 {\n width: -webkit-calc(35% - (#{$spacing-unit} / 2));\n width: calc(35% - (#{$spacing-unit} / 2));\n}\n\n.footer-col-2 {\n width: -webkit-calc(20% - (#{$spacing-unit} / 2));\n width: calc(20% - (#{$spacing-unit} / 2));\n}\n\n.footer-col-3 {\n width: -webkit-calc(45% - (#{$spacing-unit} / 2));\n width: calc(45% - (#{$spacing-unit} / 2));\n}\n\n@include media-query($on-laptop) {\n .footer-col-1,\n .footer-col-2 {\n width: -webkit-calc(50% - (#{$spacing-unit} / 2));\n width: calc(50% - (#{$spacing-unit} / 2));\n }\n\n .footer-col-3 {\n width: -webkit-calc(100% - (#{$spacing-unit} / 2));\n width: calc(100% - (#{$spacing-unit} / 2));\n }\n}\n\n@include media-query($on-palm) {\n .footer-col {\n float: none;\n width: -webkit-calc(100% - (#{$spacing-unit} / 2));\n width: calc(100% - (#{$spacing-unit} / 2));\n }\n}\n\n\n\n/**\n * Page content\n */\n.page-content {\n padding: $spacing-unit 0;\n flex: 1;\n}\n\n.page-heading {\n @include relative-font-size(2);\n}\n\n.post-list-heading {\n @include relative-font-size(1.75);\n}\n\n.post-list {\n margin-left: 0;\n list-style: none;\n\n > li {\n margin-bottom: $spacing-unit;\n }\n}\n\n.post-meta {\n font-size: $small-font-size;\n color: $grey-color;\n}\n\n.post-link {\n display: block;\n @include relative-font-size(1.5);\n}\n\n\n\n/**\n * Posts\n */\n.post-header {\n margin-bottom: $spacing-unit;\n}\n\n.post-title {\n @include relative-font-size(2.625);\n letter-spacing: -1px;\n line-height: 1;\n\n @include media-query($on-laptop) {\n @include relative-font-size(2.25);\n }\n}\n\n.post-content {\n margin-bottom: $spacing-unit;\n\n h2 {\n @include relative-font-size(2);\n\n @include media-query($on-laptop) {\n @include relative-font-size(1.75);\n }\n }\n\n h3 {\n @include relative-font-size(1.625);\n\n @include media-query($on-laptop) {\n @include relative-font-size(1.375);\n }\n }\n\n h4 {\n @include relative-font-size(1.25);\n\n @include media-query($on-laptop) {\n @include relative-font-size(1.125);\n }\n }\n}\n","/**\n * Syntax highlighting styles\n */\n.highlight {\n background: #fff;\n @extend %vertical-rhythm;\n\n .highlighter-rouge & {\n background: #eef;\n }\n\n .c { color: #998; font-style: italic } // Comment\n .err { color: #a61717; background-color: #e3d2d2 } // Error\n .k { font-weight: bold } // Keyword\n .o { font-weight: bold } // Operator\n .cm { color: #998; font-style: italic } // Comment.Multiline\n .cp { color: #999; font-weight: bold } // Comment.Preproc\n .c1 { color: #998; font-style: italic } // Comment.Single\n .cs { color: #999; font-weight: bold; font-style: italic } // Comment.Special\n .gd { color: #000; background-color: #fdd } // Generic.Deleted\n .gd .x { color: #000; background-color: #faa } // Generic.Deleted.Specific\n .ge { font-style: italic } // Generic.Emph\n .gr { color: #a00 } // Generic.Error\n .gh { color: #999 } // Generic.Heading\n .gi { color: #000; background-color: #dfd } // Generic.Inserted\n .gi .x { color: #000; background-color: #afa } // Generic.Inserted.Specific\n .go { color: #888 } // Generic.Output\n .gp { color: #555 } // Generic.Prompt\n .gs { font-weight: bold } // Generic.Strong\n .gu { color: #aaa } // Generic.Subheading\n .gt { color: #a00 } // Generic.Traceback\n .kc { font-weight: bold } // Keyword.Constant\n .kd { font-weight: bold } // Keyword.Declaration\n .kp { font-weight: bold } // Keyword.Pseudo\n .kr { font-weight: bold } // Keyword.Reserved\n .kt { color: #458; font-weight: bold } // Keyword.Type\n .m { color: #099 } // Literal.Number\n .s { color: #d14 } // Literal.String\n .na { color: #008080 } // Name.Attribute\n .nb { color: #0086B3 } // Name.Builtin\n .nc { color: #458; font-weight: bold } // Name.Class\n .no { color: #008080 } // Name.Constant\n .ni { color: #800080 } // Name.Entity\n .ne { color: #900; font-weight: bold } // Name.Exception\n .nf { color: #900; font-weight: bold } // Name.Function\n .nn { color: #555 } // Name.Namespace\n .nt { color: #000080 } // Name.Tag\n .nv { color: #008080 } // Name.Variable\n .ow { font-weight: bold } // Operator.Word\n .w { color: #bbb } // Text.Whitespace\n .mf { color: #099 } // Literal.Number.Float\n .mh { color: #099 } // Literal.Number.Hex\n .mi { color: #099 } // Literal.Number.Integer\n .mo { color: #099 } // Literal.Number.Oct\n .sb { color: #d14 } // Literal.String.Backtick\n .sc { color: #d14 } // Literal.String.Char\n .sd { color: #d14 } // Literal.String.Doc\n .s2 { color: #d14 } // Literal.String.Double\n .se { color: #d14 } // Literal.String.Escape\n .sh { color: #d14 } // Literal.String.Heredoc\n .si { color: #d14 } // Literal.String.Interpol\n .sx { color: #d14 } // Literal.String.Other\n .sr { color: #009926 } // Literal.String.Regex\n .s1 { color: #d14 } // Literal.String.Single\n .ss { color: #990073 } // Literal.String.Symbol\n .bp { color: #999 } // Name.Builtin.Pseudo\n .vc { color: #008080 } // Name.Variable.Class\n .vg { color: #008080 } // Name.Variable.Global\n .vi { color: #008080 } // Name.Variable.Instance\n .il { color: #099 } // Literal.Number.Integer.Long\n}\n"],"file":"main.css"} \ No newline at end of file diff --git a/_site/assets/markov2.png b/_site/assets/markov2.png new file mode 100644 index 0000000..0f39e8c Binary files /dev/null and b/_site/assets/markov2.png differ diff --git a/_site/assets/markov3.png b/_site/assets/markov3.png new file mode 100644 index 0000000..e341392 Binary files /dev/null and b/_site/assets/markov3.png differ diff --git a/_site/assets/minima-social-icons.svg b/_site/assets/minima-social-icons.svg new file mode 100644 index 0000000..fa7399f --- /dev/null +++ b/_site/assets/minima-social-icons.svg @@ -0,0 +1,33 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/_site/autocommit.sh b/_site/autocommit.sh new file mode 100755 index 0000000..1bb2ba3 --- /dev/null +++ b/_site/autocommit.sh @@ -0,0 +1,14 @@ +#!/bin/bash +# sleep is in seconds, to use minutes, hours, or days append m h or d like so: 10m, 3h, 4d +function commit() { + TIMESTAMP=$(date +%c) + git pull + git add . + git commit -m "Auto update $TIMESTAMP" + git push +} +while true +do +commit +sleep 60 +done diff --git a/_site/bhavya.txt b/_site/bhavya.txt new file mode 100644 index 0000000..70145c5 --- /dev/null +++ b/_site/bhavya.txt @@ -0,0 +1 @@ +My name is bhavya .I am from india and i am a boy. diff --git a/_site/bundle.sh b/_site/bundle.sh new file mode 100755 index 0000000..6ea5da5 --- /dev/null +++ b/_site/bundle.sh @@ -0,0 +1,3 @@ +bundle install +bundle add webrick +bundle exec jekyll serve --livereload diff --git a/_site/codershigh/introduction/index.html b/_site/codershigh/introduction/index.html new file mode 100644 index 0000000..6e3caf1 --- /dev/null +++ b/_site/codershigh/introduction/index.html @@ -0,0 +1,87 @@ + + + + + +Introduction | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Introduction

+
+ +
+

We will soon be composing an introduction for this initiaitve. \(a^2\) $b^45$

+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/faq/index.html b/_site/faq/index.html new file mode 100644 index 0000000..7e423b4 --- /dev/null +++ b/_site/faq/index.html @@ -0,0 +1,89 @@ + + + + + +FAQ | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

FAQ

+
+ +
+

**Where do I start from? **

+ +

This page will soon be updated.

+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/feed.xml b/_site/feed.xml new file mode 100644 index 0000000..2e8b5aa --- /dev/null +++ b/_site/feed.xml @@ -0,0 +1,40 @@ +Jekyll2023-10-15T00:06:53+05:30http://localhost:4000/codershigh/feed.xmlCoder’s HighWrite an awesome description for your new site here. You can edit this line in _config.yml. It will appear in your document head meta (for Google search results) and in your feed.xml site description.Welcome to Jekyll!2022-08-28T04:35:00+05:302022-08-28T04:35:00+05:30http://localhost:4000/codershigh/testYou’ll find this post in your _posts directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run jekyll serve, which launches a web server and auto-regenerates your site when a file is updated.

+ +

Jekyll requires blog post files to be named according to the following format:

+ +

YEAR-MONTH-DAY-title.MARKUP

+ +

Where YEAR is a four-digit number, MONTH and DAY are both two-digit numbers, and MARKUP is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works.

+ +

Jekyll also offers powerful support for code snippets:

+ +
def print_hi(name)
+  puts "Hi, #{name}"
+end
+print_hi('Tom')
+#=> prints 'Hi, Tom' to STDOUT.
+ +

Check out the Jekyll docs for more info on how to get the most out of Jekyll. File all bugs/feature requests at Jekyll’s GitHub repo. If you have questions, you can ask them on Jekyll Talk.

+ +

All is well

]]>Welcome to Jekyll!2022-08-28T04:35:00+05:302022-08-28T04:35:00+05:30http://localhost:4000/codershigh/welcome-to-jekyllYou’ll find this post in your _posts directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run jekyll serve, which launches a web server and auto-regenerates your site when a file is updated.

+ +

Jekyll requires blog post files to be named according to the following format:

+ +

YEAR-MONTH-DAY-title.MARKUP

+ +

Where YEAR is a four-digit number, MONTH and DAY are both two-digit numbers, and MARKUP is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works.

+ +

Jekyll also offers powerful support for code snippets:

+ +
def print_hi(name)
+  puts "Hi, #{name}"
+end
+print_hi('Tom')
+#=> prints 'Hi, Tom' to STDOUT.
+ +

Check out the Jekyll docs for more info on how to get the most out of Jekyll. File all bugs/feature requests at Jekyll’s GitHub repo. If you have questions, you can ask them on Jekyll Talk.

+ +

All is well

]]>Welcome to Jekyll!2022-08-28T04:35:00+05:302022-08-28T04:35:00+05:30http://localhost:4000/codershigh/My-first-postThis is my first post and I am clueless what to write. It is so nice to preach and not practice what you preach. +Isn’t this something that I should contemplate upon?

+ +

Either don’t preach, or practice what you preach :-)

]]> \ No newline at end of file diff --git a/_site/galaxy/index.html b/_site/galaxy/index.html new file mode 100644 index 0000000..9cd7f57 --- /dev/null +++ b/_site/galaxy/index.html @@ -0,0 +1,89 @@ + + + + + +Galaxy | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Galaxy

+
+ +
+ +

Coming soon.

+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/gitcommit.sh b/_site/gitcommit.sh new file mode 100755 index 0000000..712a8d7 --- /dev/null +++ b/_site/gitcommit.sh @@ -0,0 +1,5 @@ +TIMESTAMP=$(date +%c) +git pull +git add . +git commit -m "Auto update $TIMESTAMP" +git push diff --git a/_site/handbook/index.html b/_site/handbook/index.html new file mode 100644 index 0000000..11290dc --- /dev/null +++ b/_site/handbook/index.html @@ -0,0 +1,201 @@ + + + + + +Handbook | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Handbook

+
+ +
+ + +

Introduction

+ +

This is a first course in mathematics with emphasis on helping a learner with a bunch of tools and techniques required for studying several aspects of data sciences. We will illustrate the ideas through questions and puzzles. We would like to replace theorems with intuition and give pointers to inspired students to look up material for further study. By the end of the course, the student will be confident on the basics of linear algebra and probability. The course will end with a couple of exemplary ideas in data sciences and the importance of the math thus studied.

+ +

Expectations from the course

+

An important aspect of any course that is heavy on math, is to develop confidence to read up abstract material. The symbolc manipulation and logical reasoning are toolkits to infer unambiguously. It helps to stay confident and continuously interact with peers/TAs/Professor. Expect the material to be hard on your minds to begin with, but one will surely feel comfortable with time. An important tip is to take a relook at a mathematical concept multiple times, asking what is the question for which the concept is an answer. It helps to solve questions that challenge your conceptual understanding than solve multiple problems of similar type.

+ +

Grading

+

Performance Points

+ +

There will be performance points assigned to every student using the following rule:

+ + + + + + + + + + + + + + + + + + + + + + + + + + +
  
Attendance in classes/labs2 per hour
Late for the class/lab (irrespective of the urgency)-10 per class/lab
Plagiarism/Cheating/MisconductPP will drop to 0
Challenge AssignmentX
+ +
    +
  • If a student misses a lab or class, his/her \(PP\) will be uniformly distributed to the rest of the class who were present. For example in a class of 30, if 10 people are absent for a lab session, 40 \(PP\) will be distributed to the remaining 20 students. Each student will get \(\frac{40}{20}=2\).
    • +
  • A student coming late for the class, loses 10 $PP$ and this will be uniformly distributed to all those present in the class.
    • +
  • X denotes that it is discretionary. The instructor can provide challenge assignments from time to time which will add in extra PP s to your credit.
    • +
  • Plagiarism/Cheating/Misconduct will result in the reset of the performance points. It will roll back to 0. The only way we will figure out plagiarism is through viva voce.
    • +
  • The deficit \(PP\)s will be assigned by the instructor based on his discretion, evaluated based on sincerity and overall conduct.
    • +
  • This will be in practice starting from September 1st 2022.
    • +
+ +

Evaluation and Grades

+ +

Final grades will be calculated based on the following rule: +\(\left(\frac{PP}{100}.Total\right)+\left( \frac{PP}{8}\right)\)

+ +

Where PP stands for Performance Points and Total is the marks secured from theory, lab and project components.

+ +

Evaluation

+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
Type Marks
Theory InternalsInvolves theory related grading: quiz and written assignments10
Theory ExternalsFinal Theory Exam35
Lab InternalsGrading based on lab performance and viva voce10
Lab ExternalsFinal Lab Exam35
Final Project 10
+ +

Theory Assignments

+

Theory assignments will involve writeups that are mostly straight forward and will be indicative of the difficulty in the mid term and final exams. Questions for the final exam will be consequential concepts from the assignments. It would help if assignments are taken seriously for the student to secure good marks in the exams.

+ +

Lab Assignments

+

Lab assignments will involve you to work on programming based questions. These can be take home tests or in lab tests. The difficulty level is indicative of the final lab exam questions. The evaluation of lab assignments will involve a strong viva voce component.

+ +

Project

+

The student will be asked to pick a project from a list of topics. The projects will mostly be explorative in nature. Every project will be executed by a team of at most 2 people. Evaluation of the project will be based on the report and presentation.

+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/images/markov2.png b/_site/images/markov2.png new file mode 100644 index 0000000..0f39e8c Binary files /dev/null and b/_site/images/markov2.png differ diff --git a/_site/images/markov3.png b/_site/images/markov3.png new file mode 100644 index 0000000..e341392 Binary files /dev/null and b/_site/images/markov3.png differ diff --git a/_site/index.html b/_site/index.html new file mode 100644 index 0000000..04dd9c3 --- /dev/null +++ b/_site/index.html @@ -0,0 +1,84 @@ + + + + + +Coder’s High | Write an awesome description for your new site here. You can edit this line in _config.yml. It will appear in your document head meta (for Google search results) and in your feed.xml site description. + + + + + + + + + + + + + + + +
+
+

This is a homepage for the members of Coder’s High group. Check the FAQ if you are here for the first time. Check the Oceanverse and get started with your learning.

+ +

We are currently discussing Matrices

+ + + + + +
+ +
+
+ + + + + + + + + + diff --git a/_site/leastsquares/index.html b/_site/leastsquares/index.html new file mode 100644 index 0000000..879931e --- /dev/null +++ b/_site/leastsquares/index.html @@ -0,0 +1,135 @@ + + + + + +Let us Understand the Least Understood, Fair and Square! | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Let us Understand the Least Understood, Fair and Square!

+
+ +
+
    +
  1. +

    We encounter equations very often in our lives. Consider for example, the following situation at Baker’s Cafe. The manager has a very important estimate to make. Mostly, visitors at his cafe happen to be families and they are often comprised of Children and/or Adults. He observes that there are 3 adults and 1 child at a table and their bill turns out to be Rs.1200/-. There is yet another table with 2 children and 1 adult and their bill comes out to be Rs.1000/-. Can the manager estimate the consumption of a Child/Adult? This is popularly called the Simultaneous Equations and we all remember from our school days, multiple ways in which these can be solved.
    +\(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)

    +
    2. +
  2. +

    While we were taught the so called two variables and two unknowns, what if there were more equations than unknowns?
    +\(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)
    +\(1A + 1C = 900\)

    +
    3. +
  3. +

    Note that the previous question can be modelled as a matrix:

    + +

    \(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)
    +\(1A + 1C = 900\)

    + +

    Observe this is same as :

    + +

    \(\left( \begin{matrix} 3 & 1 \\1 & 2 \\1 & 1 \\\end{matrix}\right)\) +\(\left( +\begin{matrix} +B\\ +C\\ +\end{matrix} +\right)\) += +\(\left( + \begin{matrix} + 1200\\ + 1000\\ + 900\\ + \end{matrix} +\right)\)

    +
    4. +
  4. +

    The best way to solve is, is to guess the values :-). Can you write a python code to guess the values?

    +
    5. +
  5. +

    How do you solve this mathematically? There are two nice ways of solving this:

    +
      +
    • Model this as a question of inverting a rectangular matrix and find the solution. (Whoa! my teacher never taught me that!)
      • +
    • Model this as a funtion of two variables and solve it using partial differentiation (Eeks!)
      • +
    +
    6. +
+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/linalg75/index.html b/_site/linalg75/index.html new file mode 100644 index 0000000..160ca0c --- /dev/null +++ b/_site/linalg75/index.html @@ -0,0 +1,674 @@ + + + + + +Oceanverse | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Oceanverse

+
+ +
+ + +

Linear Algebra

+ +
    +
  1. Consider the matrix +\(\left[ \begin{array}{cc} +1 & 2\\ 3 & 4 +\end{array}\right]\) +
      +
    • What does it remind you of?
      • +
    • What does it denote?
      • +
    • Where and why do we use a matrix?
      • +
    • Can you enlist a few applications of matrices?
      +
      • +
    +
    2. +
  2. +

    Define a function. What is a surjective, injective and bijective +function?

    +
    3. +
  3. +

    Given an example of a function +\(f:\mathbb{R}^2\rightarrow\mathbb{R}^2\)

    +
    4. +
  4. Given an example of a very nice function +\(f:\mathbb{R}^2\rightarrow\mathbb{R}^2\) +
      +
    • Make extra efforts to make this function really nice.
      • +
    • Explain what is so nice about your +function?
      • +
    • Why should one study such functions?
      +
      • +
    +
    5. +
  5. Define a function +\(\phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2\), which satisfies the following property: The point \(\phi(2,3)=(7,4)\). Note that this function should be defined at all points on \(\mathbb{R}^2\). +
      +
    • What are the properties of your function? Observe it +microscopically.
      +
      • +
    +
    6. +
  6. +

    Given a function \(\phi : \mathbb{R}^2 \rightarrow \mathbb{R}^2\) +which satisfies the following two conditions:

    + +\[\phi(u+v)=\phi(u) +\phi(v)\] + +\[\phi(\alpha v)=\alpha\phi(v)\] + +
      +
    • What can one say of such functions?
      • +
    • Observe this function closely, such functions form the crux of several discplines, mainly of sciences and engineering. Spend at least 20 minutes dissecting them to the best possible extent.
      +
      • +
    +
    7. +
  7. +

    Consider \(\mathbb{R}^2\) what are all the properties of this set? +\(\mathbb{R}^2\) is called a space of all vectors, aka a vector space. +Lookup for the definition of a vector space.

    +
    8. +
  8. +

    A subset of a vector space which in itself is a vector space is +caled a subspace. Given an example of a subspace of \(\mathbb{R}^2\).

    +
    9. +
  9. +

    Given a vector \((1,7)\) what does the set +\(\{ \alpha(1,7) | \alpha \in \mathbb{R}\}\) represent? Is it a +subspace of \(\mathbb{R}^2\)?

    +
    10. +
  10. +

    Is \(\mathbb{R}^3\) a vector space?

    +
    11. +
  11. +

    Conside the two points \((1,2,3)\) and \((4,5,7)\in \mathbb{R}^3\). What +does the following set denote: +\(\{\alpha(1,2,3)+\beta(4,5,7) | \alpha, \beta \in \mathbb{R}\}\). +Is this a subspace?

    +
    12. +
  12. +

    Consider a straight line \(y=2x+1\) in \(\mathbb{R}^2\), does it form a +subspace of \(\mathbb{R}^2\)?

    +
    13. +
  13. +

    Consider a unit circle in \(\mathbb{R}^2\), centered at origin, is it +a subspace of \(\mathbb{R}^2\)?

    +
    14. +
  14. +

    What are all the subspaces of \(\mathbb{R}^2\)?

    +
    15. +
  15. +

    What are all the subspaces of \(\mathbb{R}^3\)?

    +
    16. +
  16. +

    Given \(\mathbb{R}^3\), pick any two points \(u,v\in \mathbb{R}^3\). +Note that \(\{\alpha u+\beta v | \alpha, \beta \in \mathbb{R}\}\) is a +subspace of \(\mathbb{R}^3\). Generalize this idea!

    +
    17. +
  17. +

    The set \(\{\alpha u + \beta v | \alpha, \beta \in \mathbb{R}\}\) is +called the linear combination of vectors \(u\) and \(v\). We can +generalize this to \(k\) vectors. Observe what this set is all about?

    +
    18. +
  18. +

    We say that a vector \(w\) is manufactured by \(u\) and \(v\) if +\(w\in \{\alpha u +\beta v | \alpha, \beta \in \mathbb{R} \}\).

    +
    19. +
  19. +

    Show that \((1,2,3)\) and \((4,5,6)\) can manufacture \((7,8,9)\). Also +\((4,5,6)\) and \((7,8,9)\) can manufacture \((1,2,3)\). Finally \((4,5,6)\) +can be manufactured by the other two vectors.

    +
    20. +
  20. +

    Can \((2,1,0)\) and \((3,0,8)\) manufacture \((1,1,1)\) ?

    +
    21. +
  21. +

    Can \((0,0,1)\) and \((0,1,0)\) manufacture \((1,0,0)\)?

    +
    22. +
  22. +

    When can two vectors in \(\mathbb{R}^3\) manufacture a given third +vector?

    +
    23. +
  23. +

    When can two vectors in \(\mathbb{R}^3\) fail to manufacture a given +third vector?

    +
    24. +
  24. +

    If \(\{u,v,w\}\) are such that a vector in this set can be +manufactured by some vectors in the same set, then such a set is +called a linearly dependent set.

    +
    25. +
  25. +

    Give examples of a linearly dependent set in \(\mathbb{R}^3\) and get +conversant with the definition.

    +
    26. +
  26. +

    If \(\{u,v,w\}\) are such that no vector in this set can be +manufactured by any combination of vectors in the same set, then such +a set is called a linearly independent set.

    +
    27. +
  27. +

    Give examples of a linearly dependent set in \(\mathbb{R}^3\) and +\(\mathbb{R}^2\) and get conversant with the definition.

    +
    28. +
  28. +

    Are \((1,2), (3,4)\) linearly independent in \(\mathbb{R}^2\)? Prove!

    +
    29. +
  29. +

    Are \((1,1),(2,3),(7,17)\) Linearly Independent or Dependent?

    +
    30. +
  30. +
      +
    • +

      Construct a set of 3 vectors that are Linearly Independent in +\(\mathbb{R}^2\). Can you?

      +
      • +
    • +

      Construct a set of 3 vectors that are Linearly Independent in +\(\mathbb{R}^3\). Can you?

      +
      • +
    • +

      Construct a set of \(k\) vectors that are Linearly Independent in +\(\mathbb{R}^k\). Can you?

      +
      • +
    • +

      Construct a set of \(k+1\) vectors that are Linearly Independent in +\(\mathbb{R}^k\). Can you?

      +
      • +
    +
    31. +
  31. +
      +
    • +

      Show that in \(\mathbb{R}^2\) we can at most have 2 Linearly +Independent vectors.

      +
      • +
    • +

      Show that in \(\mathbb{R}^3\) we can at most have 3 Linearly +Independent vectors.

      +
      • +
    • +

      Show that in \(\mathbb{R}^n\) we can at most have \(n\) Linearly +Independent vectors.

      +
      • +
    +
    32. +
  32. +

    Set of any two linearly independent vectors in \(\mathbb{R}^2\) is +called a basis. Set of any three linearly independent vectors in +\(\mathbb{R}^3\) is called a basis. Similarly, for \(n\).

    +
    33. +
  33. +

    Show that a basis can manufacture any vector of the vector +space.

    +
    34. +
  34. +

    Show that any set of linearly independent vectors form a subset of +some basis. In other words, one can include a few more elements to a +linearly independent set and make it a basis.

    +
    35. +
  35. +

    Show that the number of elements in any basis for a given vector +space is always constant.

    +
    36. +
  36. +

    Try taking a few vectors in \(\mathbb{R}^3\) and discuss its linear +independence or linear dependence. Try atleast 10 examples and +familiarize yourself.

    +
    37. +
  37. +

    Show that any 3 vectors on a plane passing through the origin in +\(\mathbb{R}^3\) cannot be linearly independent. Prove.

    +
    38. +
  38. +

    What are all the subspaces of \(R^3\).

    +
    39. +
  39. +

    Consider a subspace of \(R^3\) and write down its basis. Do this for 3 +to 4 different subspaces.

    +
    40. +
  40. +

    Give an example of a function +\(f:\mathbb{R}^2 \rightarrow \mathbb{R}^2\) such that the range of the +function is the straight line \(y=10x\).

    +
    41. +
  41. +

    As an example consider the following basis set of +\(\mathbb{R}^2 : \left \{(1,2),(2,2)\right \}\). Construct a function +\(\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2\) such that:

    + +\[\phi(u+v)=\phi(u)+\phi(v)\] + +\[\phi(\alpha u)= \alpha \phi(u)\] + +

    Such a function is called a LT function,

    + +
      +
    • +

      Where is (1,2) and (2,2) mapped?

      +
      • +
    • +

      Where is (1,0) and (0,1) mapped?

      +
      • +
    • +

      What is the range of this function?

      +
      • +
    +
    42. +
  42. +

    Consider a function \(\phi\) which is LT which maps

    + +\[\phi(1,2)=(3,4)\] + +\[\phi(6,6)= (2,0)\] + +
      +
    • +

      How many such functions can you construct?

      +
      • +
    • +

      What is the range of this function?

      +
      • +
    +
    43. +
  43. +

    Discuss the range of the following functions, given their values at +a few points:

    + +

    \(\phi(1,2)=(3,4)\) \(\&\) \(\phi(1,1)=(6,8)\)

    + +

    \(\phi(1,1)=(2,2)\) \(\&\) \(\phi(3,3)=(4,4)\)

    + +

    \(\phi(1,2)=(3,5)\) \(\&\) \(\phi(0,8)=(3,0)\)

    + +

    \(\phi(-2,2)=(0,0)\) \(\&\) \(\phi(8,2)=(1,1)\)

    + +

    \(\phi(1,1)=(2,2)\) \(\&\) \(\phi(1,2)=(3,3)\)

    +
    44. +
  44. +

    Give an example of an LT function which maps a L.I. set of vectors +to a L.I. set of vectors i.e. +\(\phi:\mathbb{R}^2 \rightarrow \mathbb{R}^2\), where +\(\left \{ u,v \right \}\) are L.I. \(\&\) +\(\left \{\phi(u), \phi(v)\right \}\) are also L.I.

    +
    45. +
  45. +

    Same as the previous question, but \(\left \{ u,v \right \}\) is L.I. +and \(\left \{\phi(u), \phi(v)\right \}\) is L.D.
    +What can one say about the range?

    +
    46. +
  46. +

    Note that range of a L.I function is always a subspace.

    +
    47. +
  47. +

    Note that the set N=\(\{v: \phi(v)=0\}\) is a subspace of \(R^2\) where +\(\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2\) is L.I . Take atleast 5 +different examples of L.I functions and see if this is true. The set +\(N\subseteq Domain\) is called the null space of \(\phi\).

    +
    48. +
  48. +

    Construct a Linear Transformation +\(\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2\), +\(\phi(0,1)=(3,4)\) and \(\phi(1,0)=(1,2)\). Construct an inverse of +linear transformation and observe it carefully. Is it a L.T function +too?

    +
    49. +
  49. +

    Do you realize the importance of inverting a matrix?

    +
    50. +
  50. +

    L.T stands for Linear Transformation .It is aka a matrix.

    +
    51. +
  51. +

    Define a L.T. \(\phi:\mathbb{R}^2\rightarrow \mathbb{R}^2\) such that +\(\phi(0,1)=(2,3)\) and \(\phi(1,0)=(7,4)\). This function \(\phi\) is same +as the matrix \(\begin{bmatrix} +7 & 2 \\ +4 & 3 +\end{bmatrix}\). +
    \(\phi(x,y)\) is same as \(\begin{bmatrix} +7 & 2 \\ +4 & 3 +\end{bmatrix}\) \(\begin{bmatrix} +x\\y +\end{bmatrix}\), Verify and make your share of observations.
    +What is +\(\phi^{-1}\) ? Is this the traditional matrix inverse? +
    Think !

    +
    52. +
  52. +

    Consider a L.T. \(\phi\) such that : \(\phi(1,2)=(3,5)\) and +\(\phi(3,1)=(8,2)\). What is the matrix equivalent of \(\phi\) ?

    +
    53. +
  53. Solve the following : +
      +
    • +\[\begin{array} 3x-2y=15 \\ x+4y=19 \end{array}\] +
      • +
    • +

      Isn’t this the same as \(\begin{bmatrix} +1 & -2 \\ +1 & 4 +\end{bmatrix}\) \(\begin{bmatrix} +x\\y +\end{bmatrix}\) = \(\begin{bmatrix} +15\\19 +\end{bmatrix}\)

      +
      • +
    • +

      You are trying to find if there is an element in the domain +which maps to (15,19) .

      +
      • +
    • what exactly is happening here ? (Say all that you can)
      • +
    + +


    +
    54. +
  54. +

    Given \(V_{1}\) , \(V_{2}\) & \(V_{3}\) are L.I. , S.T.

    + +
      +
    • +

      \(\left \{ V_{2} - V_{3} , V_{1} - V_{3} , V_{1} - V_{2} \right \}\) +are L.D.

      +
      • +
    • +

      \(\left \{ V_{1} + V_{2} , V_{1} + V_{3} , V_{2} + V_{3} \right \}\) +are L.I.

      +
      • +
    +
    55. +
  55. +

    Given vectors \(\left \{ V_{1} , V_{2} , V_{3} , V_{4} \right \}\) +their sum is 0 = \(V_{1}\) + \(V_{2}\) + \(V_{3}\) + \(V_{4}\) . Is this set +L.I or L.D. ?

    +
    56. +
  56. +

    Show that the following are equivalent:

    + +
      +
    • +

      The vectors \(\{v_1,v_2,\dots, v_n\}\) are linearly independent.

      +
      • +
    • +

      \(\forall \alpha_1, \alpha_2, \dots, \alpha_n \in \mathbb{R}\ \left( \sum_{i=1}^{n} \alpha_i v_i = 0 \implies \alpha_j = 0\ \forall 1 \leq j \leq n\right)\).

      +
      • +
    +
    57. +
  57. +

    In the following six matrices find out the following:

    + +
      +
    1. +

      Rank of the matrix

      +
      2. +
    2. +

      Dimension of the range

      + +
        +
      1. +\[\left[ \begin{array}{cc} +1 & 2\\ 2 & 4 +\end{array}\right]\] +
        2. +
      2. +\[\left[ \begin{array}{cc} +1 & 2\\ 3 & 4 +\end{array}\right]\] +
        3. +
      3. +\[\left[ \begin{array}{cc} +7 & -7\\ 2 & -2 +\end{array}\right]\] +
        4. +
      4. +\[\left[ \begin{array}{cc} +0 & 1\\ 1 & 0 +\end{array}\right]\] +
        5. +
      5. +\[\left[ \begin{array}{cc} +1 & 1\\ 3 & 3 +\end{array}\right]\] +
        6. +
      6. +\[\left[ \begin{array}{ccc} +1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 +\end{array}\right]\] +
        7. +
      +
      3. +
    + +

    What is happening here? Describe in detail.

    +
    58. +
  58. +

    The dimension of the range of the matrix \(M\) and \(M^{T}\) is always +the same. Why?

    +
    59. +
  59. +

    Take three linearly independent vectors in \(\mathbb{R}^3\). Show that +they form a basis of \(\mathbb{R}^3\).

    +
    60. +
  60. +

    Consider the matrix \(\left[ \begin{array}{ccc} +1 & 4 & 7\\ 2 & 5 & 8 \\ 3 & 6 & 9 +\end{array}\right]\). The dimension of the range is 2. The range of +this linear transformation is obviously a linear combination of +three vectors. Do you see which are those three vectors?

    +
    61. +
  61. +

    Consider any \(2 \times 2\) matrix. Do you observe that the :

    + +

    Dimension of the Null space & the Dimension of the range are in someway related?

    +
    62. +
  62. +

    What about a \(3 \times 3\) matrix?

    +
    63. +
  63. +

    Can you generalise this to an \(n\times n\) matrix?

    +
    64. +
  64. +

    When is a L.T. function one-one and when is it onto?

    +
    65. +
  65. +

    A \(2\times 2\) matrix A can be seen as two vectors placed as columns. For +example \((1,2)\) and \((3,4)\) when placed as columns give rise to the +matrix \(\begin{bmatrix} +1 & 3 \\ +2 & 4 +\end{bmatrix}\).

    + +

    Note that \(\begin{bmatrix} +1 & 3 \\ +2 & 4 +\end{bmatrix}\) \(\begin{bmatrix} +\alpha \\ +\beta +\end{bmatrix}\) \(\in\) +\({\{ \alpha(1,2)+\beta(3,4) : \alpha, \beta \in \mathbb{R} \} }\).

    + +

    Note that matrix, \(\begin{bmatrix} +a & b \\ +c & d +\end{bmatrix}\) \(\begin{bmatrix} +x \\ +y +\end{bmatrix}\) simply is \(x(a,c)+y(b,d)\).

    + +

    Note that a matrix takes a vector \((x,y)\) to a linear combination of +the column vectors.

    + +

    It is now clear that the range of the matrix, say\(\begin{bmatrix} +1 & 1 & 4 \\ +0 & 2 & 4 \\ +1 & 3 & 4 +\end{bmatrix}\) is nothing but the linear combination of the vectors +\((1,0,1), (1,2,3), (4,4,4)\).

    +
    66. +
  66. +

    Consider a \(10\times 10\) matrix \(A\), defined as following:

    + +

    \(A[i,j] = 0\) if \(i+j\cong 0(mod2)\)

    + +

    \(A[i,j] = 1\) if \(i+j\cong 1(mod2)\)

    + +

    What is the dimension of the range?

    +
    67. +
  67. +

    Consider the sub-space \(S:(y=13x)\) of \(\mathbb{R}^2\)

    + +
      +
    • +

      Give an example of a \(\phi\) such that \(S\) is its null space.

      +
      • +
    • +

      Give an example of a \(\phi\) such that S is the the + range of \(\phi\).

      +
      • +
    +
    68. +
  68. +

    Let \(A =\) +\(\begin{bmatrix} +1 & 3 \\ +2 & 4 +\end{bmatrix}\)

    + +
      +
    • +

      Show that the null space of \(A \subset\) Null space of \(A^2\)

      +
      • +
    • +

      Is this true for any \(2\times 2\) matrix.

      +
      • +
    • +

      Is this true for any \(3\times3\) matrix.

      +
      • +
    • +

      Is this true for any \(n\times n\) matrix.

      +
      • +
    +
    69. +
  69. +

    Define column space. S.T. Column space of \(A^2 \subset\) Column space +of \(A\).

    +
    70. +
  70. Solve the following simultaneous equation: +
    +
      +
    • +\[\begin{array} _x + 4y + 7z =9\\ +2x + 5y + 8z = 9\\ +3x +6y + 9z = 9 +\end{array}\] +
      • +
    • What is the null space of \(\begin{bmatrix} + 1 & 4 & 7 \\ + 2 & 5 & 8 \\ + 3 & 6 & 9 + \end{bmatrix}\)
      • +
    • The above two questions are strongly related and + make a theory. What is your obseration?
      • +
    +
    71. +
  71. +

    What does one mean by the linear combination of vectors and what is a +linear span?

    +
    72. +
  72. +

    Show that, if a matrix \(A\) has linearly independent column vectors, +then the columns of the matrix \(A^2\) are also linearly independent.

    +
    73. +
  73. +

    \(Ax = Ay \iff x=y\) . Is this true? If False, when is the statement +False and what leads to the falsity of the statement?

    +
    74. +
  74. +

    Let \(M\) be a \(3\times 3\) matrix, such that, the dim(Range) =3. Show +that, \(M^2 = M \iff M\) is an identity matrix.

    +
    75. +
  75. Consider a \(10 \times 10\) matrix with all its entries to be \(1\). +What is the dimension of its range?
    76. +
+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/links/index.html b/_site/links/index.html new file mode 100644 index 0000000..b321625 --- /dev/null +++ b/_site/links/index.html @@ -0,0 +1,97 @@ + + + + + +Links | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Links

+
+ +
+
    +
  1. +

    Watch these videos without fail. This is a good intuitive introduction to linear algebra.

    +
    2. +
  2. +

    These Videos make an essential introduction to calculus.

    +
    3. +
  3. +

    Here is a complete course on linear algebra from MIT OCW. It is the most popular resource for the subject.

    +
    4. +
+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/matrixmystics/index.html b/_site/matrixmystics/index.html new file mode 100644 index 0000000..3c65cbe --- /dev/null +++ b/_site/matrixmystics/index.html @@ -0,0 +1,357 @@ + + + + + +Matrix Mystics | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Matrix Mystics

+
+ +
+ +

Module 1

+ +
+ +
    +
  1. +

    Ram and Lakshman were two brothers, Ram’s pocket money was twice as much as Lakshman. The good boy that Ram and Lakshman were, they did not spend their pocket money on anything. They instead saved the same in their piggy bank. Every week, they would check their savings so far. Assume the first week’s savings was \((R_1,L_1)\) and second week’s \((R_2,L_2)\) and so on. They try plotting their weekly savings on a graph sheet. How will the points look like?

    +
    2. +
  2. +

    Atul’s house is centered at origin \((0,0)\) he walks straight (along the x-axis) for 2 units and then takes a left and walks 1 unit to reach Bala’s house, after that he takes a right turn and walks for one unit and then a left turn and walks for one unit and reaches Chetan’s house. He continues in a similar style, takes a right turn 1 unit and then left turn one unit and reaches Divya’s house. Are the houses of Bala, Chetan and Divya on a straight line? What is the equation of this line? Plot this on Geogebra

    +
    3. +
  3. +

    Plot the lines \(y=x\), \(y=2x\), \(y=10x\).

    +
    4. +
  4. +

    Observe that they all pass through the origin. Why?

    +
    5. +
  5. +

    Plot \(y=2x+1\). Why doesn’t it pass through the origin?

    +
    6. +
  6. +

    Plot \(y=ax+b\), with \(a\) and \(b\) as parameters which you should be able to varry. What do youaa observe?

    +
    7. +
  7. +

    Consider the following simultaneous equation:

    + +

    \(2x+3y=7\)
    +\(3x+4y=10\)

    + +

    Do you see a 2x2 matrix here? What is the importance of seeing a matrix in this problem? Why study matrices in general?
    Do you observe that this problem can be retold as:
    \(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right)\) +\(\left( +\begin{matrix} +x\\ +y\\ +\end{matrix} +\right)\) +=\(\left( +\begin{matrix} +7\\ +10\\ +\end{matrix} +\right)\)

    +
    8. +
  8. +

    Consider a simple function \(f(x) = 3x+2\). This function is invertible right? Can you tell us what is \(\alpha\) such that \(f(\alpha)=17\)? Is such an \(\alpha\) unique? How did you find such an \(\alpha?\). Is this always possible?

    +
    9. +
  9. +

    Consider the function \(f(x)=x^2-10\), what is f(5)?

    +
    10. +
  10. +

    Consider the function \(f(x)=x^2-10\), if \(f(\alpha)=54\), what is \(\alpha\)?

    +
    11. +
  11. +

    Consider the function \(g(x)=x^3-x^2-10x+2\), if \(g(x)=-22\) what is \(x\)?

    +
    12. +
  12. +

    Do you know what is \(\mathbb{R}, \mathbb{R}^2 and \mathbb{R}^3\) ?

    +
    13. +
  13. +

    Consider the function \(\phi : \mathbb{R}^2\rightarrow \mathbb{R}^2\) defined by \(\phi (x,y)=(2x+3y,3x+4y)\). What has this to do with the previous question?

    +
    14. +
  14. +

    Is the function \(\phi\) invertible? In the question above on matrices, we see that it is of the form \(Ax=b\). Note that we can invert the matrix, using the method that was taught to us in our high school to find out the value for the variables x and y. This is one of the many applications of matrices.

    +
    15. +
  15. +

    We will now see matrices as functions. Instead of \(\phi\) we will write the matrix itself:
    \(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2\).

    +
    16. +
  16. +

    Consider the function \(\left( \begin{matrix} 1 & 2 \\2 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2\). This matrix takes a few elements to the origin. What are those elements? Plot this using Geogebra.

    +
    17. +
+ +

Module 2

+ +
+ +
    +
  1. A is assigned 0, B:1, C:2, and so on up to Z:25
    +Assume you denoted every letter with a number, as given in the table above.
    You need to encrypt the word “SUDARSHANA” which stands for the numbers: \(18, 20, 3, 0, 17, 18, 7, 0, 13,0\).
    +You encrypt this using a matrix given by : \(\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right)\).
    +So “SUDARSHANA” will end up becoming: \(96, 134, 6, 9, 88, 123, 14, 21, 26, 39\).
    +Given these numbers, how will you decrypt the message and get back “SUDARSHANA”?
    . This is a well known cryptographic protocol called the Hill Cipher. You can read more online.
    2. +
  2. +

    We encounter equations very often in our lives. Consider for example, the following situation at Baker’s Cafe. The manager has a very important estimate to make. Mostly, visitors at his cafe happen to be families and they are often comprised of Children and/or Adults. He observes that there are 3 adults and 1 child at a table and their bill turns out to be Rs.1200/-. There is yet another table with 2 children and 1 adult and their bill comes out to be Rs.1000/-. Can the manager estimate the consumption of a Child/Adult? This is popularly called the Simultaneous Equations and we all remember from our school days, multiple ways in which these can be solved.
    +\(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)

    +
    3. +
  3. +

    While we were taught the so called two variables and two unknowns, what if there were more equations than unknowns?
    +\(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)
    +\(1A + 1C = 900\)

    +
    4. +
  4. +

    Note that the previous question can be modelled as a matrix:

    + +

    \(3A + 1C = 1200\)
    +\(1A + 2C = 1000\)
    +\(1A + 1C = 900\)

    + +

    Observe this is same as :

    + +

    \(\left( \begin{matrix} 3 & 1 \\1 & 2 \\1 & 1 \\\end{matrix}\right)\) +\(\left( +\begin{matrix} +A\\ +C\\ +\end{matrix} +\right)\) += +\(\left( + \begin{matrix} + 1200\\ + 1000\\ + 900\\ + \end{matrix} +\right)\)

    +
    5. +
  5. +

    One obvious way to solve this, is to guess the values :-). Can you get closer to the solution by guessing? Note that there is no solution to this question. You can just reduce the error. Do you see why?

    +
    6. +
  6. +

    In the figure below: +fig1 +If 1000 people were to start in one state, what will be the distribution of people eventually?

    +
    7. +
  7. In the figure below: +fig2 +If 1000 people were to start in one state, what will be the distribution of people eventually?
    8. +
+ +

Module 3

+ +
+ +
    +
  1. +

    Use Geogebra: +Draw the vector \(\begin{bmatrix}1 \\ +1 \\ +\end{bmatrix}\). Find out all those vectors which are perpendicular to this vector.

    +
    2. +
  2. +

    Do you observe that we are asking for vectors \(\begin{bmatrix}x \\ +y \\ +\end{bmatrix}\) such that, +\(\begin{bmatrix}x & y \\ +\end{bmatrix} \begin{bmatrix} 1\\ 1 \\ \end{bmatrix}=0\)

    +
    3. +
  3. +

    Use Geogebra and solve the above question with \(\begin{bmatrix} 1 \\ +1 \\ +\end{bmatrix}\) replaced by \(\begin{bmatrix}a \\ +b \\ +\end{bmatrix}\).Use \((a,b)\) as parameters and check what happens to \((x,y)\).

    +
    4. +
  4. +

    What is \((x,y,z)\) satisfying the following equation? (Use Geogebra) +\(\begin{bmatrix}x & y & z\\ +\end{bmatrix} \begin{bmatrix} 1\\ 2 \\ 3\\ \end{bmatrix}=0\)

    +
    5. +
  5. +

    Use Geogebra and plot all the points in the set below. +\(T= \{ \beta(1,2,1) | \beta \in \mathbb{R}\}\)

    +
    6. +
  6. +

    Use Geogebra and plot all the points in the set below. +\(S= \{ \beta(2,7.3) | \beta \in \mathbb{R}\}\)

    +
    7. +
  7. +

    Use Geogebra and plot all the points in the set below. +\(W= \{\alpha(1,2,1) + \beta(2,7.3) | \alpha,\beta \in \mathbb{R}\}\)

    +
    8. +
  8. +

    In the above set W find out all the points satisfying \((x,y,z)\) satisfying the following: (Use Geogebra) +\(\begin{bmatrix}w1 & w2 & w3\\ +\end{bmatrix} \begin{bmatrix} x\\ y \\ z\\ \end{bmatrix}=0\) + where \((w1,w2,w3) \in \mathbb W\)

    +
    9. +
  9. +

    Given the matrix \(A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}\), find out all the possible \((x,y,z)\) such that: +\(\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix}=0\) + Observe carefully, what has this question got to do with previous five questions in this module

    +
    10. +
  10. +

    Given the matrix \(A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}\) what does the following three sets represent?
    +(i) \(\mathscr{R}=\{\alpha(1,2,3) + \beta(4,5,6) + \gamma(7,8,9) |\alpha, \beta, \gamma\in \mathbb{R}\}\)
    +(ii) \(C=\{\alpha(1,4,7) + \beta(2,5,8) + \gamma(3,6,9) | \alpha, \beta, \gamma \in \mathbb{R}\}\)
    +(iii) \(N=\{(x,y,z)|x(1,4,7) + y(2,5,8) + z(3,6,9) = 0 \}\)
    + Use only Geogebra :)

    +
    11. +
  11. +

    Did you observe that every vector of \(\mathscr{R}\) is perpendicular to every vector of \(N\)?

    +
    12. +
  12. +

    Consider the matrix \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}\). Draw the line \(2y+x=4\). Seeing the matrix \(B\) as a function \(B:\mathbb{R^2}\mapsto \mathbb{R^2}\),
    where does \(B\) takes the line \(2y+x=4\)?
    +Where does it take:
    +i)\(2y+x=10\)
    +ii)\(2y+x=62\)
    +iii)\(2y+x=1800\)

    +
    13. +
  13. +

    In general \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\), where does this function take \(2y+x=k\)?(where \(k\) is a constant)

    +
    14. +
  14. +

    Given \(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\). What is the range of this function?

    +
    15. +
  15. +

    You have achieved the required wisdom if you have realized that:
    +\(B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}\).

    +
    16. +
+ +

Module 4

+ +
    +
  1. +

    Given the matrix \(M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}\). Use Geogebra to plot \(\mathscr{R}\), \(\mathscr{C}\) & \(\mathscr{N}\). what do you observe?
    +(i) \(\mathscr{R}=\{\alpha(1,3) + \beta(2,6) | \alpha, \beta\in \mathbb{R}\}\)
    +(ii) \(\mathscr{C}=\{\alpha(1,2) + \beta(3,6) | \alpha, \beta\in \mathbb{R}\}\)
    +(iii) \(\mathscr{N}=\{(x,y)| x(1,3) + y(2,6) = 0, \forall x,y\in \mathbb{R} \}\)

    +
    2. +
  2. +

    Note that \(\mathscr{R}\) and \(\mathscr{N}\) are orthogonal.

    +
    3. +
  3. +

    What is the null-space of \(M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}\) & the null-space of \(M^T\)?

    +
    4. +
  4. +

    Do you observe that \(C(M)\) ⊥ \(N(M^T)\)   \(R(M)\) ⊥ \(N(M^T)\) ?

    +
    5. +
  5. +

    Consider \(A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}\). What is \(N(A)\), \(C(A)\), \(R(A)\), \(N(A^T)\).

    +
    6. +
  6. +

    Consider a 4x4 matrix \(M\): \(\mathbb{R^4}\mapsto \mathbb{R^4}\) whose range is
    +a) \(4-Dimension\)
    +b) \(3-Dimension\)
    +c) \(2-Dimension\)
    +d) \(1-Dimension\)
    +e) \(0-Dimension\)
    +Give an example each for all the above 5 cases.

    +
    7. +
  7. +

    Consider \(A : \mathbb{R^{3}} \to \mathbb{R^{3}}\)
    +a) S.T. if the range contains a point \((a,b,c)\), then it should contain the entire set $S$, defined by: +\(S= \{\alpha(a, b,c)/ \alpha \in \mathbb{R}\}\).
    +b) S.T. if the range contains the points \((a,b,c)\) and \((d,e,f)\), then the range contains the entire set \(T\) defined by: +\(T=\{\alpha(a,b,c) + \beta(d,e,f) \thinspace/\thinspace \alpha,\beta\in \mathbb{R}\}\).
    +c) Note: \(S\) is of the dimension \(1\), but \(T\) need’nt be of dimension \(2\). Think!

    +
    8. +
+ +

Module 5

+ +

1) Give an example of two $2-dim$ subspaces in $\mathbb{R^{3}}$. Let us call it $S_1, S_2$

+ +

2) Let $S_3$ be all those vectors perpendicular to $S_1$. $S_4$ be that of $S_2$

+ +

3)Find a matrix M whose Null-Space is $S_3$. column space is $S_2$

+ +

4)What does $S_1$ $S_4$ represent

+ +

5) Do you observe there is a bijection from $S_1 \to S_4$

+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/new_post/index.html b/_site/new_post/index.html new file mode 100644 index 0000000..027389e --- /dev/null +++ b/_site/new_post/index.html @@ -0,0 +1,93 @@ + + + + + +Welcome to Jekyll! | Coder’s High + + + + + + + + + + + + + + + + +
+
+
+ +
+

Welcome to Jekyll!

+

+

+
+ +
+

This is my first post and I am clueless what to write. It is so nice to preach and not practice what you preach. +Isn’t this something that I should contemplate upon?

+ +

Either don’t preach, or practice what you preach :-)

+ +
+
+ +
+
+ + + + + + + + + + diff --git a/_site/oceanverse/index.html b/_site/oceanverse/index.html new file mode 100644 index 0000000..c534c51 --- /dev/null +++ b/_site/oceanverse/index.html @@ -0,0 +1,258 @@ + + + + + +Oceanverse | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Oceanverse

+
+ +
+ + +

Ocean Part 1

+ +

1. Write a program that prints “Namasthey India” to the screen (1 point).

+ +

2. Take as input a number \(n\) and print the square, cube and \(2^n\) of the number (1 point).

+ +

3. Print the following using four print statements:

+
*
+**
+***
+****
+
+

(1 point) .

+ +

4. Write an interactive python program which does the following:

+
What's your name? John
+How old are you? 25
+What's your favorite color? Blue
+What's your favorite hobby? Reading
+
+

(1 point).

+ +

5. Understand how to use a if conditional in python. Ask the user to enter a number and check if the number is even or odd (1 point).

+ +

6. Write a program to take as input a number \(n\) and display the first \(n\) natural numbers (1 point).

+ +

7. Print a sequence of numbers starting from the number a with common difference d. Go on till you reach the number b.

+
Enter a value for a: 10
+Enter a value for d: 3
+Enter a value for b: 20
+Output: 10 13 16 19
+
+

(1 point).

+ +

8. Write a program that calculates and prints the sum of all numbers from 1 to n, where n is provided by the user (1 point).

+ +

9. Write a program that takes a number n from the user and prints the multiplication table for that number from 1 to 10. Generalize it from \(i\) to \(j\).

+
2X1=2
+2X2=4
+and so on...
+
+

(1 point).

+ +

10. Write a program to find out if the given number is prime or not (1 point).

+ +

Ocean Part 2

+ +

11. Write a program to take as input \(n\) and print all prime numbers upto and including \(n\) (1 point).

+ +

12. Input two different strings and concatenate it (1 point).

+ +

13. Take two strings of the same length and intersperse the second one into the first one:

+
Input:
+india
+super
+Output:
+isnudpiear
+
+

(1 point).

+ +

14. Given a string, write a program to reverse it (1 point).

+ +

15. Given a string, check if it is a palindrome or not (1 point).

+ +

16. Write a program that counts and prints the number of vowels and the number of consonants in the string (1 point).

+ +

17. List of Squares: Write a program that prints the square of numbers from 1 to n, where n is provided by the user (1 point).

+ +

18. Fibonacci Sequence : Write a program that prints the first n numbers in Fibonacci numbers (1 point).

+ +

19. Print Star Pattern: Write a program that takes a number n from the user and prints a right-angled triangle pattern with stars of n rows (1 point) .

+ +

20. Write a piece of code which does exactly as specified in this video (10 points).

+ +

21. Factorial: Write a program that calculates the factorial of a number provided by the user (1 point).

+ +

22. Positive or Negative: Write a program that asks the user for a number and prints whether the number is positive, negative, or zero (1 point).

+ +

23. Simple Interest Calculation: Write a program that calculates the simple interest for given principal, rate, and time provided by the user (1 point).

+ +

24. Temperature Converter: Write a program that converts Celsius to Fahrenheit or Fahrenheit to Celsius, depending on user input (1 point).

+ +

25. Leap Year or Not: Write a program that checks if a given year is a leap year or not. Google for the details on how to figure out if the given number is a leap year or not. It is more complicated than simply checking for a multiple of 4 (1 point).

+ +

26. Divisible by 7 and 5: Write a program that checks if a number provided by the user is divisible by both 7 and 5. Generalize it to a and b (1 point).

+ +

27. Create a Python program that prompts the user for their age. If the age is less than 18, print “You are a minor.” If the age is between 18 and 65, print “You are an adult.” Otherwise, print “You are a senior citizen.” (1 point).

+ +

28. Grading System: Write a program that takes the marks of five subjects from the user and calculates the grade according to the average marks: +A if average >= 90 +B if average >= 80 and < 90 +C if average >= 70 and < 80 +D if average >= 60 and < 70 +F otherwise +(1 point).

+ +

29. Decimal to Binary Conversion: Write a program that converts a decimal number to its binary representation using loops, without using built-in conversion functions (1 point).

+ +

30. Write a program that finds the gcd of two numbers using Euclid’s Algrorithm. Given \(k\) as an input, display those two numbers, both with \(k\) digits, such that they take the maximum number of steps to find the GCD, across all the pair of numbers, both of which are of \(k\) digits (8 points).

+ +

31. Write a program to populate a list \(L\) with the first \(n\) natural numbers (1 point).

+ +

32. Write a program to populate a list \(L\) with random numbers in the range 1 to 1000 (1 point).

+ +

Ocean Part 3

+

(Watch these videos, as and when required)

+ +

33. Write a function called add that takes two numbers as arguments and returns their sum. (1 point)

+ +

34. Write a function called factorial that takes an integer n and returns the factorial of n. (1 point)

+ +

35. Write a function called fibonacci that takes an integer n and returns the n-th number in the Fibonacci sequence. (1 point)

+ +

36. Write a function which simulates the process of throwing \(n\) identical balls into \(n\) bins. What is the maximum across the buckets? Write a short report on the output of your code. (2 points)

+ +

37. Write a function which simulates the process of throwing identical balls into \(n\) identical bins until all the bins are non-empty. How many balls are we expected to throw? Investigate and write a short report based on your observation. (2 points)

+ +

38. Checking for Even or Odd: Write a function called is_even that takes an integer and returns True if the number is even, and False if it is odd. (1 point)

+ +

39. Calculate Area of a Circle: Write a function called circle_area that takes the radius of a circle as an argument and returns its area. (1 point)

+ +

40. Write a function that displays the spiral: RULLDDRRRUUULLLL… and so on. It should keep displaying until it has displayed 1,000,000 Letters in this pattern. (5 points)

+ +

41. Concatenating Strings: Write a function called concatenate that takes two strings and returns them concatenated together with a space between them. (1 point)

+ +

42. Finding the Maximum: Write a function called find_max that takes a list of numbers and returns the largest number in the list. (1 point)

+ +

43. Consider the sensex data from here. Consider only the end of the day closing values. When should you have bought and when should you have sold in order to gain the maximum return in this 30 year period? You can assume that you can buy the stocks partially and you start with, let us say 1,00,000 Rupees. (10 points)

+ +

44. Consider the data of Height and Weight of 25,000 people as available here. Is the data correlated? What is the correlation? Can you plot the points and fit a line? You are free to use any built in functions, but you should know what the functions are doing. Correlation is a statistical concept which you may know from your high school, we only expect you to understand this concept at an intuitive level. (5 point)

+ +

Ocean Part 4

+ +

45. Reading exercise (first few chapters of Algorithms to live by). (25 points)

+ +

46. Write a function that takes as inputs list of lists that depicts square matrices A and B and then gives us the sum. (1 point)

+ +

47. Write a function that takes as inputs list of lists that depicts square matrices A and B and then gives us the product. (2 points)

+ +

48. Write a function that writes the first n numbers and writes it to a file by name output.txt (1 point)

+ +

49. Write a function that reads a file which has numbers in each line and outputs it on the screen one by one. (1 point)

+ +

50. Solve this question. (10 points)

+ +

51. Write a program to sort a list of numbers using the bubble sort technique. (1 point)

+ +

52. Write a program to sort a list of numbers using the merge sort technique. (2 point)

+ +

53. Write a program to sort a list of numbers using the quick sort technique. (2 point)

+ +

54. Write a program to search for an element in a list using Binary Search.(2 point)

+ +

55. Write a program which, given a text file comprising of all words in lower case, one word per line, sorts this file using bubble sort, merge sort and quick sort. Which technique is the fastest and why? Write a detailed report. (5 points)

+ +

56. Write a program to find the median element in a list of unsorted elements. You are not supposed to sort the list. (2 points)

+ +

57. Solve the contiguous sum sub array problem (1 point).

+ +

58. We solved the SFC question a while ago. Can you solve this on similar lines? (2 points)

+ +

59. Write a program to encrypt a string using caesar cipher. (1 point)

+ +

60. Read and Solve this (20 points)

+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/one_post.html b/_site/one_post.html new file mode 100644 index 0000000..20ceb31 --- /dev/null +++ b/_site/one_post.html @@ -0,0 +1,108 @@ + + + + + +Welcome to Jekyll! | Coder’s High + + + + + + + + + + + + + + + + +
+
+
+ +
+

Welcome to Jekyll!

+

+

+
+ +
+

You’ll find this post in your _posts directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run jekyll serve, which launches a web server and auto-regenerates your site when a file is updated.

+ +

Jekyll requires blog post files to be named according to the following format:

+ +

YEAR-MONTH-DAY-title.MARKUP

+ +

Where YEAR is a four-digit number, MONTH and DAY are both two-digit numbers, and MARKUP is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works.

+ +

Jekyll also offers powerful support for code snippets:

+ +
def print_hi(name)
+  puts "Hi, #{name}"
+end
+print_hi('Tom')
+#=> prints 'Hi, Tom' to STDOUT.
+ +

Check out the Jekyll docs for more info on how to get the most out of Jekyll. File all bugs/feature requests at Jekyll’s GitHub repo. If you have questions, you can ask them on Jekyll Talk.

+ +

All is well

+ +
+
+ +
+
+ + + + + + + + + + diff --git a/_site/pagerank/index.html b/_site/pagerank/index.html new file mode 100644 index 0000000..f7995b8 --- /dev/null +++ b/_site/pagerank/index.html @@ -0,0 +1,117 @@ + + + + + +Pagerank | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Pagerank

+
+ +
+
    +
  1. Consider any \(2\times 2\) matrix A and apply the matrix on a \(2\times1\) vector \(v\). Keep applying this matrix and notice that the direction converges, while the magnitude may get larger. Keep normalizing \(v\) and notice the direction to which it converges. Use Numpy
    2. +
  2. +

    Consider the previous \(2\times 2\) matrix and find out its eigenvalue and eigenvectors. What do you observe?

    +
    3. +
  3. +

    Consider the following network: +NetworkAssign values to the nodes so that the value of the nodes = sum of the values of the nodes from which there are incoming edges. For example the value of F should be half of the value of C. The value of E should be half the value of B and so on.

    +
    4. +
  4. +

    Write down the edge list of the above graph and use networkx to run a random walk on it. What is the distribution of visits?

    +
    5. +
  5. +

    Are the following two questions equivalent?:

    + +
      +
    • +

      If I were to give pocket money to two of my daughters: 500 rupees each.

      +
      • +
    • +

      I toss a coin and give my elder daughter 1000 rupees if its heads or the younger daughter 1000 rupees if its tails.

      + +

      Are these two statements equivalent? In the sense that, by the end of the year, do you think both my daughters would have received, more or less, the same amount of money?

      +
      • +
    +
    6. +
  6. +

    Consider the adjacency matrix of the above graph, tweak it and observe that the principal eigen vector is same as the answer to the previous question. (Principal Eigen Vector is defined as the eigen vector corresponding to the highest eigen value)

    +
    7. +
  7. Can you consider a network of vertices, in the order of thousands and figure out the answer? You will observe that the best method to use is the random walk (with teleportation). why?
    8. +
+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/questionverse.html b/_site/questionverse.html new file mode 100644 index 0000000..c1c54a2 --- /dev/null +++ b/_site/questionverse.html @@ -0,0 +1,162 @@ + + + + + +Questionverse | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Questionverse

+
+ +
+

Chapter 1: Warmup

+ +
    +
  1. +

    What is the intuition for this infinite series being equal to 1? \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots\)

    +
    2. +
  2. +

    Fact: \(\frac{1}{1-x} = 1+x+x^2+x^3+\dots\). Is this always true?

    +
    3. +
  3. +

    Note that \(e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!}\dots\). Why is this number important? Can you notice that this number is obviously greater than 1? Can you show that it is actually less than 3?

    +
    4. +
  4. +

    Note that \(e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!}\dots\). What is the significance of this?

    +
    5. +
  5. +

    Understand Binomial Theorem and show that \(\left( 1+\frac{1}{n}\right)^n = e)\)

    +
    6. +
  6. +

    If you keep compounding your money, when will it get doubled? (Hint: \(\left( 1+\frac{1}{n}\right)^n = e)\))

    +
    7. +
  7. +

    If you keep spending your money by \(\epsilon\) proportion, when will your money get to less than a rupee?

    +
    8. +
  8. +

    If you consider a 1000 meter long stick and randomly break it at some point, what do you expect the length to be, of the smaller part and the bigger part?

    +
    9. +
  9. +

    A bus conductor charges 1000 rupees per seat. The bus can accommodate 100 people. If \(k\) number of seats are empty, the conductor levies a penalty of \(10k\) on each passenger. For example, if 5 seats are empty, the conductor will charge 1050 for the 95 passengers who are present. What is the number of passengers for which the conductor earns the maximum money?

    +
    10. +
  10. +

    Understand the Monty Hall problem.

    +
    11. +
  11. +

    What is the importance of a matrix? Where do we use them?

    +
    12. +
  12. +

    What is the intuitive idea of an inverse of a matrix?

    +
    13. +
  13. +

    In the following code, what is the probability that \(a\), \(b\) and \(c\) form the sides of a triangle?

    + + 
    import random
+a=random.random()
+b=random.random()
+c=random.random()
+
    +
    14. +
  14. +

    Show that \(sqrt(2)\) is irrational.

    +
    15. +
  15. +

    Show that prime numbers are infinite.

    +
    16. +
  16. +

    You know the old school way of adding, subtracting, multiplying and dividing 2 big numbers. Can you provide a proof for these methods?

    +
    17. +
  17. +

    Find the GCD of two big numbers using only a calculator. What method helps you calculate the GCD fast? How do you know that the method works? Can you figure out the number of steps it takes to arrive at a solution?

    +
    18. +
  18. +

    Describe Birthday Paradox. Write a piece of python code to figure out the probability of you finding same birthdays in a class of \(n\) people. Plot the probability on the \(Y\) axis and the number of people in the class \(n\) in the \(X\) axis. How does the curve look like?

    +
    19. +
  19. +

    After programmatically understanding the birthday paradox, can you understand it mathematically?

    +
    20. +
  20. +

    When you distribute \(n\) chocolates to \(n\) people uniformly at random, many of them may end up getting more than one chocolate. How many people, on an average, end up getting no chocolates at all.

    +
    21. +
+ + + + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/sem975/index.html b/_site/sem975/index.html new file mode 100644 index 0000000..9c5ef84 --- /dev/null +++ b/_site/sem975/index.html @@ -0,0 +1,101 @@ + + + + + +Semester 9.75 | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Semester 9.75

+
+ +
+
    +
  1. This is an initiative comprising of 6 students.
    2. +
  2. We call this Semester 9 three quarters.
    3. +
  3. We all know that \((a+b)^2=a^2+b^2+2ab\)
    4. +
  4. We all know that The binomial theorem states that for any real numbers ( a ) and ( b ), and any non-negative integer ( n ):
    5. +
+ +

\((a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k\)

+
    +
  1. My name is bhavya Rao
    2. +
  2. I am at iitropar
    3. +
  3. I am sitting next to adithya and yatri
    4. +
  4. Atharva is infront of me.
    5. +
  5. Atharva is infront of me.
    6. +
+ +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/syllabus/index.html b/_site/syllabus/index.html new file mode 100644 index 0000000..f20d5a8 --- /dev/null +++ b/_site/syllabus/index.html @@ -0,0 +1,139 @@ + + + + + +Syllabus | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Syllabus

+
+ +
+

The following syllabus is only indicative of the topics we will be covering. We may not follow this sequence. The teaching style will be illustrative and not enumerative.

+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
Sl. No.Topic
1Introduction to Mathematical Thinking
2A Gentle Introduction to Probability
3Random Variables and Expectations
4Distributions: Binomial, Bernoulli, Gaussian & Poisson
5Markov Chains
6Introduction to Matrices
7Linearly Independent and Dependent Vectors
8Linear Transformations
9Matrix Factorization
10Applications: Dimensionality Reduction, Recommender Systems, Pagerank, Support Vector Machines
+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/test.txt b/_site/test.txt new file mode 100644 index 0000000..038d718 --- /dev/null +++ b/_site/test.txt @@ -0,0 +1 @@ +testing diff --git a/_site/todo/index.html b/_site/todo/index.html new file mode 100644 index 0000000..93631f9 --- /dev/null +++ b/_site/todo/index.html @@ -0,0 +1,115 @@ + + + + + +Todo | Coder’s High + + + + + + + + + + + + + + + +
+
+
+ +
+

Todo

+
+ +
+

@TAs

+ +

Note: Leave it to me if you cannot cover some of the topics.

+ +

ToDo for TAs

+ +
    +
  1. Session on basic probability (absolute minimals).
    2. +
  2. Session on functions. How to find minima/maxima of a function.
    3. +
  3. Session on Geogebra.
    4. +
  4. Teach them: +
      +
    • Matrix multiplication.
      • +
    • Determinants.
      • +
    • Geometrical meaning of dot product.
      • +
    • Matrix Inverse.
      • +
    • Finding Eigen Values and Eigen Vectors. + (All of these should be for 2x2 matrices only). + Refer to 3blue1brown’s youtube channel. Refer to his linear algebra vidoes. They are short and sweet.
      • +
    +
    5. +
+ +

Project Component

+

There is a project for 10 marks. Feel free to give them some reading or programming assignment based on the math concepts taught.

+ +

Regards,
+Sudarshan

+ + +
+ +
+ +
+
+ + + + + + + + + + diff --git a/_site/two_post.html b/_site/two_post.html new file mode 100644 index 0000000..e7d218b --- /dev/null +++ b/_site/two_post.html @@ -0,0 +1,108 @@ + + + + + +Welcome to Jekyll! | Coder’s High + + + + + + + + + + + + + + + + +
+
+
+ +
+

Welcome to Jekyll!

+

+

+
+ +
+

You’ll find this post in your _posts directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run jekyll serve, which launches a web server and auto-regenerates your site when a file is updated.

+ +

Jekyll requires blog post files to be named according to the following format:

+ +

YEAR-MONTH-DAY-title.MARKUP

+ +

Where YEAR is a four-digit number, MONTH and DAY are both two-digit numbers, and MARKUP is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works.

+ +

Jekyll also offers powerful support for code snippets:

+ +
def print_hi(name)
+  puts "Hi, #{name}"
+end
+print_hi('Tom')
+#=> prints 'Hi, Tom' to STDOUT.
+ +

Check out the Jekyll docs for more info on how to get the most out of Jekyll. File all bugs/feature requests at Jekyll’s GitHub repo. If you have questions, you can ask them on Jekyll Talk.

+ +

All is well

+ +
+
+ +
+
+ + + + + + + + + + diff --git a/assets/christ.jpg b/assets/christ.jpg new file mode 100644 index 0000000..bb61a7a Binary files /dev/null and b/assets/christ.jpg differ diff --git a/assets/main.scss b/assets/main.scss new file mode 100644 index 0000000..c60ebe4 --- /dev/null +++ b/assets/main.scss @@ -0,0 +1,5 @@ +--- +# Only the main Sass file needs front matter (the dashes are enough) +--- + +@import "minima"; diff --git a/assets/markov2.png b/assets/markov2.png new file mode 100644 index 0000000..0f39e8c Binary files /dev/null and b/assets/markov2.png differ diff --git a/assets/markov3.png b/assets/markov3.png new file mode 100644 index 0000000..e341392 Binary files /dev/null and b/assets/markov3.png differ diff --git a/assets/minima-social-icons.svg b/assets/minima-social-icons.svg new file mode 100644 index 0000000..fa7399f --- /dev/null +++ b/assets/minima-social-icons.svg @@ -0,0 +1,33 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/autocommit.sh b/autocommit.sh new file mode 100755 index 0000000..1bb2ba3 --- /dev/null +++ b/autocommit.sh @@ -0,0 +1,14 @@ +#!/bin/bash +# sleep is in seconds, to use minutes, hours, or days append m h or d like so: 10m, 3h, 4d +function commit() { + TIMESTAMP=$(date +%c) + git pull + git add . + git commit -m "Auto update $TIMESTAMP" + git push +} +while true +do +commit +sleep 60 +done diff --git a/bhavya.txt b/bhavya.txt new file mode 100644 index 0000000..70145c5 --- /dev/null +++ b/bhavya.txt @@ -0,0 +1 @@ +My name is bhavya .I am from india and i am a boy. diff --git a/bundle.sh b/bundle.sh new file mode 100755 index 0000000..6ea5da5 --- /dev/null +++ b/bundle.sh @@ -0,0 +1,3 @@ +bundle install +bundle add webrick +bundle exec jekyll serve --livereload diff --git a/gitcommit.sh b/gitcommit.sh new file mode 100755 index 0000000..712a8d7 --- /dev/null +++ b/gitcommit.sh @@ -0,0 +1,5 @@ +TIMESTAMP=$(date +%c) +git pull +git add . +git commit -m "Auto update $TIMESTAMP" +git push diff --git a/images/markov2.png b/images/markov2.png new file mode 100644 index 0000000..0f39e8c Binary files /dev/null and b/images/markov2.png differ diff --git a/images/markov3.png b/images/markov3.png new file mode 100644 index 0000000..e341392 Binary files /dev/null and b/images/markov3.png differ diff --git a/index.markdown b/index.markdown new file mode 100644 index 0000000..aa7ded1 --- /dev/null +++ b/index.markdown @@ -0,0 +1,10 @@ +--- +# Feel free to add content and custom Front Matter to this file. +# To modify the layout, see https://jekyllrb.com/docs/themes/#overriding-theme-defaults + +layout: home +--- + +This is a homepage for the members of Coder's High group. Check the [FAQ](/codershigh/faq/) if you are here for the first time. Check the [Oceanverse](/codershigh/oceanverse/) and get started with your learning. + +We are currently discussing [Matrices](/codershigh/matrixmystics/) diff --git a/matrixmystics.md b/matrixmystics.md new file mode 100644 index 0000000..591214b --- /dev/null +++ b/matrixmystics.md @@ -0,0 +1,233 @@ +--- +layout: page +title: Matrix Mystics +order: 5 +permalink: /matrixmystics/ +--- + +* TOC +{:toc} +# Module 1 + + +___ + +1. Ram and Lakshman were two brothers, Ram's pocket money was twice as much as Lakshman. The good boy that Ram and Lakshman were, they did not spend their pocket money on anything. They instead saved the same in their piggy bank. Every week, they would check their savings so far. Assume the first week's savings was $$(R_1,L_1)$$ and second week's $$(R_2,L_2)$$ and so on. They try plotting their weekly savings on a graph sheet. How will the points look like? + +2. Atul's house is centered at origin $$(0,0)$$ he walks straight (along the x-axis) for 2 units and then takes a left and walks 1 unit to reach Bala's house, after that he takes a right turn and walks for one unit and then a left turn and walks for one unit and reaches Chetan's house. He continues in a similar style, takes a right turn 1 unit and then left turn one unit and reaches Divya's house. Are the houses of Bala, Chetan and Divya on a straight line? What is the equation of this line? Plot this on Geogebra + + + +3. Plot the lines $$y=x$$, $$y=2x$$, $$y=10x$$. + +4. Observe that they all pass through the origin. Why? + +5. Plot $$y=2x+1$$. Observe, Why doesn't it pass through the origin? + +6. Plot $$y=ax+b$$, with $$a$$ and $$b$$ as parameters which you should be able to vary. What do you observe? + +7. Consider the following simultaneous equation: + + $$2x+3y=7$$
+ $$3x+4y=10$$
+ + Do you see a 2x2 matrix here? What is the importance of seeing a matrix in this problem? Why study matrices in general?
Do you observe that this problem can be retold as:
$$ \left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right) $$ + $$\left( + \begin{matrix} + x\\ + y\\ + \end{matrix} + \right)$$ + =$$\left( + \begin{matrix} + 7\\ + 10\\ + \end{matrix} + \right)$$ +8. Consider a simple function $$f(x) = 3x+2$$. This function is invertible right? Can you tell us what is $$\alpha$$ such that $$f(\alpha)=17$$? Is such an $$\alpha$$ unique? How did you find such an $$\alpha?$$. Is this always possible? + +9. Consider the function $$f(x)=x^2-10$$, what is $$f(5)$$? + +10. Consider the function $$f(x)=x^2-10$$, if $$f(\alpha)=54$$, what is $$\alpha$$? + +11. Consider the function $$g(x)=x^3-x^2-10x+2$$, if $$g(x)=-22$$ what is $$x$$? + + +12. Do you know what is $$\mathbb{R}, \mathbb{R}^2 and\ \mathbb{R}^3$$ ? + + +13. Consider the function $$\phi : \mathbb{R}^2\rightarrow \mathbb{R}^2$$ defined by $$\phi (x,y)=(2x+3y,3x+4y)$$. What has this to do with the previous question? + +14. Is the function $$\phi$$ invertible? In the question above on matrices, we see that it is of the form $$A\vec{x}=b$$. Note that we can invert the matrix, using the method that was taught to us in our high school to find out the value for the variables $$x$$ and $$y$$. This is one of the many applications of matrices. + +15. We will now see matrices as functions. Instead of $$\phi$$ we will write the matrix itself:
$$\left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2$$. + +16. Consider the function $$\left( \begin{matrix} 1 & 2 \\2 & 4 \\\end{matrix}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}^2$$. This matrix takes a few elements to the origin. What are those elements? Plot this using Geogebra. + + + +# Module 2 + +--- + +1. $$A$$ is assigned $$0$$, $$B:1$$, $$C:2$$, and so on up to $$Z:25$$
+Assume you denoted every letter with a number, as given in the table above.
You need to encrypt the word $$SUDARSHANA$$ which stands for the numbers: $$18, 20, 3, 0, 17, 18, 7, 0, 13,0$$.
+You encrypt this using a matrix given by : $$ \left( \begin{matrix} 2 & 3 \\3 & 4 \\\end{matrix}\right) $$.
+So $$SUDARSHANA$$ will end up becoming: $$96, 134, 6, 9, 88, 123, 14, 21, 26, 39$$.
+Given these numbers, how will you decrypt the message and get back $$SUDARSHANA$$?
. This is a well known cryptographic protocol called the Hill Cipher. You can read more online. +1. We encounter equations very often in our lives. Consider for example, the following situation at ___Baker's Cafe___. The manager has a very important estimate to make. Mostly, visitors at his cafe happen to be families and they are often comprised of Children and/or Adults. He observes that there are 3 adults and 1 child at a table and their bill turns out to be Rs.1200/-. There is yet another table with 2 children and 1 adult and their bill comes out to be Rs.1000/-. Can the manager estimate the consumption of a Child/Adult? This is popularly called the _Simultaneous Equations_ and we all remember from our school days, multiple ways in which these can be solved.
+ $$ 3A + 1C = 1200 $$ + $$ 1A + 2C = 1000 $$ + +2. While we were taught the so called two variables and two unknowns, what if there were more equations than unknowns?
+ $$ 3A + 1C = 1200 $$ + $$ 1A + 2C = 1000 $$ + $$ 1A + 1C = 900 $$ + +3. Note that the previous question can be modelled as a matrix: + + $$ 3A + 1C = 1200 $$ + $$ 1A + 2C = 1000 $$ + $$ 1A + 1C = 900 $$ + + Observe this is same as : + + $$ \left( \begin{matrix} 3 & 1 \\1 & 2 \\1 & 1 \\\end{matrix}\right) $$ + $$\left( + \begin{matrix} + A\\ + C\\ + \end{matrix} + \right)$$ + = +$$ +\left( + \begin{matrix} + 1200\\ + 1000\\ + 900\\ + \end{matrix} + \right) +$$ + + + +4. One obvious way to solve this, is to guess the values :-). Can you get closer to the solution by guessing? Note that there is no solution to this question. You can just reduce the error. Do you see why? + +5. In the figure below: +![fig1](/codershigh/assets/markov2.png) +If 1000 people were to start in one state, what will be the distribution of people eventually? + +5. In the figure below: +![fig2](/codershigh/assets/markov3.png) +If 1000 people were to start in one state, what will be the distribution of people eventually? + +# Module 3 + +___ + +1. Use Geogebra: +Draw the vector $$\begin{bmatrix}1 \\ +1 \\ +\end{bmatrix}$$. Find out all those vectors which are perpendicular to this vector. + +2. Do you observe that we are asking for vectors $$\begin{bmatrix}x \\ +y \\ +\end{bmatrix}$$ such that, +$$\begin{bmatrix}1 & 1 \\ +\end{bmatrix} \begin{bmatrix} x\\ y \\ \end{bmatrix}=0 $$ + +3. Use Geogebra and solve the above question with $$\begin{bmatrix} 1 \\ +1 \\ +\end{bmatrix}$$ replaced by $$\begin{bmatrix}a \\ +b \\ +\end{bmatrix}$$.Use $$(a,b)$$ as parameters and check what happens to $$(x,y)$$. + +4. What is $$(x,y,z)$$ satisfying the following equation? (Use Geogebra) +$$\begin{bmatrix}1 & 2 & 3\\ +\end{bmatrix} \begin{bmatrix} x\\ y \\ z\\ \end{bmatrix}=0 $$ + +5. Use Geogebra and plot all the points in the set below. +$$T= \{ \alpha(1,2,1) | \alpha \in \mathbb{R}\} $$ + +6. Use Geogebra and plot all the points in the set below. +$$S= \{ \beta(2,7,3) | \beta \in \mathbb{R}\} $$ + +7. Use Geogebra and plot all the points in the set below. +$$W= \{\alpha(1,2,1) + \beta(2,7,3) | \alpha,\beta \in \mathbb{R}\} $$ + +8. In the above set $$W$$ find out all the points $$(x,y,z)$$ satisfying the following: (Use Geogebra) +$$\begin{bmatrix}w_1 & w_2 & w_3\\ +\end{bmatrix} \begin{bmatrix} x\\ y \\ z\\ \end{bmatrix}=0 $$ + where $$(w_1,w_2,w_3) \in W$$. Note that $$w_i$$s are real numbers. + +9. Given the matrix $$A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}$$, find out all the possible $$(x,y,z)$$ such that: +$$ \begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix}=0$$ + Observe carefully, what has this question got to do with previous five questions in this module + +10. Given the matrix $$A=\begin{bmatrix}1 & 2 & 3\\ 4 & 5 &6\\ 7 & 8 & 9\\ \end{bmatrix}$$ what does the following three sets represent?
+(i) $$\mathscr{R}=\{\alpha(1,2,3) + \beta(4,5,6) + \gamma(7,8,9) |\alpha, \beta, \gamma\in \mathbb{R}\} $$
+(ii) $$C=\{\alpha(1,4,7) + \beta(2,5,8) + \gamma(3,6,9) | \alpha, \beta, \gamma \in \mathbb{R}\}$$
+(iii) $$N=\{(x,y,z)|x(1,4,7) + y(2,5,8) + z(3,6,9) = 0 \}$$
+ Use only Geogebra :) + +11. Did you observe that every vector of $$\mathscr{R}$$ is perpendicular to every vector of $$N$$? + +12. Consider the matrix $$B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}$$. Draw the line $$2y+x=4$$. Seeing the matrix $$B$$ as a function $$B:\mathbb{R^2}\mapsto \mathbb{R^2}$$,
where does $$B$$ takes the line $$2y+x=4$$?
+Where does it take:
+i)$$2y+x=10$$
+ii)$$2y+x=62$$
+iii)$$2y+x=1800$$ + +13. In general $$B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}$$, where does this function take $$2y+x=k$$?(where $$k$$ is a constant) + +14. Given $$B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}$$. What is the range of this function? + +15. You have achieved the required wisdom if you have realized that:
+$$B=\begin{bmatrix} 1 & 2 \\ 2 & 4\\ \end{bmatrix}:\mathbb{R^2}\mapsto \mathbb{R^2}$$.
+" $$B$$ collapses a dimension ".
+ +# Module 4 + +1. Given the matrix $$M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}$$. Use Geogebra to plot $$\mathscr{R}$$, $$\mathscr{C}$$ & $$\mathscr{N}$$. what do you observe?
+(i) $$\mathscr{R}=\{\alpha(1,3) + \beta(2,6) | \alpha, \beta\in \mathbb{R}\} $$
+(ii) $$\mathscr{C}=\{\alpha(1,2) + \beta(3,6) | \alpha, \beta\in \mathbb{R}\} $$
+(iii) $$\mathscr{N}=\{(x,y)| x(1,3) + y(2,6) = 0, \forall x,y\in \mathbb{R} \}$$
+ +2. Note that $$\mathscr{R}$$ and $$\mathscr{N}$$ are orthogonal.
+ +3. What is the null-space of $$M=\begin{bmatrix} 1 & 3 \\ 2 & 6\\ \end{bmatrix}$$ & the null-space of $$M^T$$?
+ +4. Do you observe that $$C(M)$$ ⊥ $$N(M^T)$$ ,   $$R(M)$$ ⊥ $$N(M)$$ ?
+ +5. Consider $$A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}$$. What is $$N(A)$$, $$C(A)$$, $$R(A)$$, $$N(A^T)$$.
+ +6. Consider a 4x4 matrix $$M$$: $$\mathbb{R^4}\mapsto \mathbb{R^4}$$ whose range is
+a) $$4-Dimension$$
+b) $$3-Dimension$$
+c) $$2-Dimension$$
+d) $$1-Dimension$$
+e) $$0-Dimension$$
+Give an example each for all the above 5 cases.
+ +7. Consider $$A : \mathbb{R^{3}} \to \mathbb{R^{3}} $$
+a) Show that if the range contains a point $$(a,b,c)$$, then it should contain the entire set $$S$$, defined by: +$$S= \{\alpha(a, b,c)| \alpha \in \mathbb{R}\}$$.
+b) Show that if the range contains the points $$(a,b,c)$$ and $$(d,e,f)$$, then the range contains the entire set $$T$$ defined by: +$$T=\{\alpha(a,b,c) + \beta(d,e,f) \thinspace|\thinspace \alpha,\beta\in \mathbb{R}\}$$.
+c) Note: $$S$$ is of the dimension $$1$$, but $$T$$ need'nt be of dimension $$2$$. Think! + +# Module 5 + +1. Give an example of two $$2-dim$$ subspaces in $$\mathbb{R^{3}}$$. Let us call it $$S_1, S_2$$. + + +2. Let $$S_3$$ be all those vectors perpendicular to $$S_1$$. $$S_4$$ be that of $$S_2$$. + + +3. Find a matrix $$M$$ whose Null-Space is $$S_3$$. column space is $$S_2$$. + + +4. What does $$S_1$$ and $$S_4$$ represent? + +5. Do you observe there is a bijection from $$S_1 \to S_2$$? diff --git a/sem975.md b/sem975.md new file mode 100644 index 0000000..ca4e95e --- /dev/null +++ b/sem975.md @@ -0,0 +1,17 @@ +--- +layout: page +title: Semester 9.75 +permalink: /sem975/ +--- + +1. This is an initiative comprising of 6 students. +2. We call this *Semester 9 three quarters*. +3. We all know that $$(a+b)^2=a^2+b^2+2ab$$ +4. We all know that The binomial theorem states that for any real numbers \( a \) and \( b \), and any non-negative integer \( n \): + +$$ (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$$ +5. My name is bhavya Rao +6. I am at iitropar +7. I am sitting next to adithya and yatri +8. Atharva is infront of me. +8. Atharva is infront of me. diff --git a/test.txt b/test.txt new file mode 100644 index 0000000..038d718 --- /dev/null +++ b/test.txt @@ -0,0 +1 @@ +testing