参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
求高度还是求深度,你搞懂了不?
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
返回 false 。
咋眼一看这道题目和104.二叉树的最大深度很像,其实有很大区别。
这里强调一波概念:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
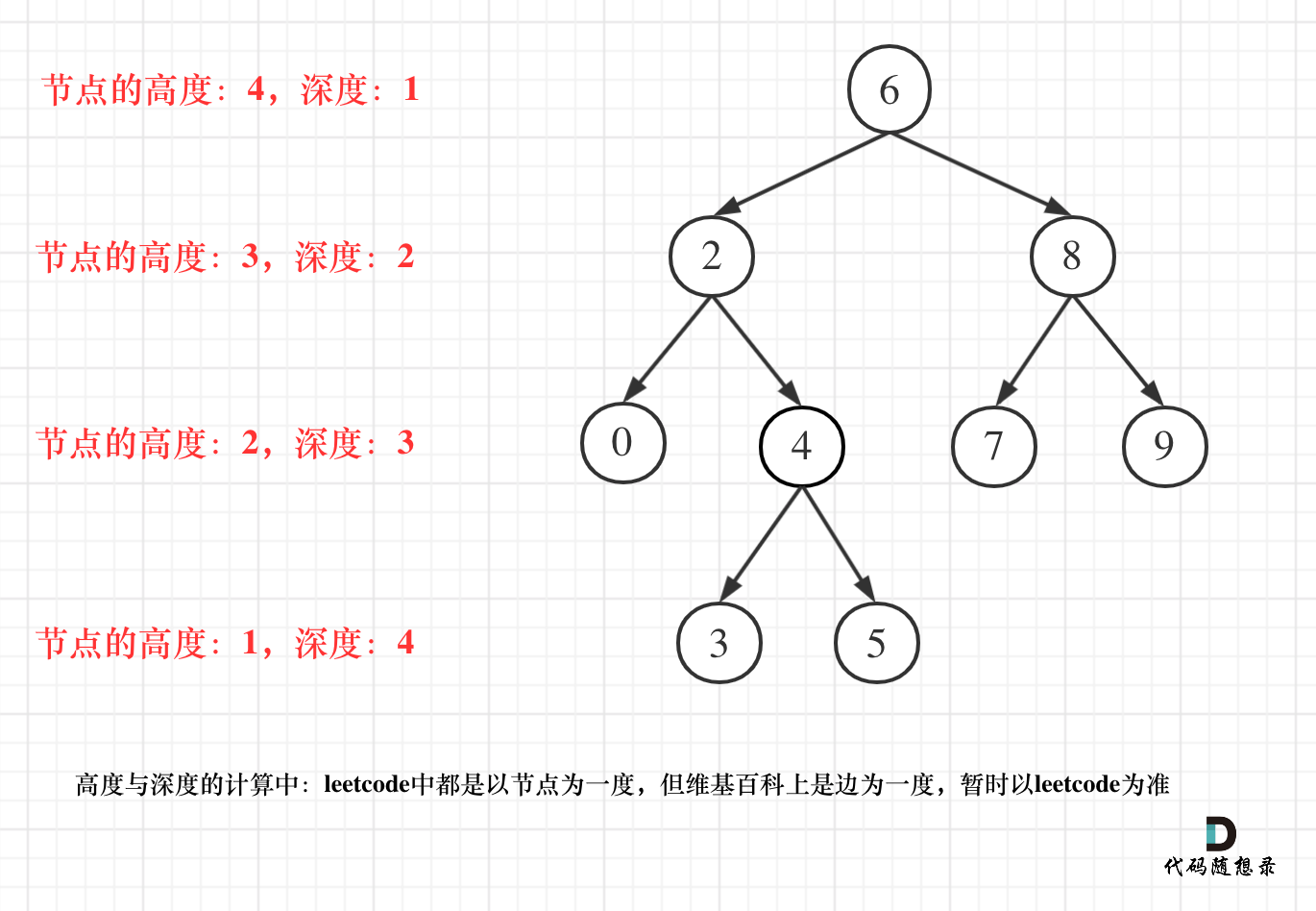
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:
关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
有的同学一定疑惑,为什么104.二叉树的最大深度中求的是二叉树的最大深度,也用的是后序遍历。
那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这颗树的最大深度,所以才可以使用后序遍历。
在104.二叉树的最大深度中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
class Solution {
public:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
depth++; // 深度+1
getDepth(node->left, depth);
depth--; // 回溯,深度-1
}
if (node->right) { // 右
depth++; // 深度+1
getDepth(node->right, depth);
depth--; // 回溯,深度-1
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == NULL) return result;
getDepth(root, 1);
return result;
}
};可以看出使用了前序(中左右)的遍历顺序,这才是真正求深度的逻辑!
注意以上代码是为了把细节体现出来,简化一下代码如下:
class Solution {
public:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
getDepth(node->left, depth + 1);
}
if (node->right) { // 右
getDepth(node->right, depth + 1);
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == 0) return result;
getDepth(root, 1);
return result;
}
};此时大家应该明白了既然要求比较高度,必然是要后序遍历。
递归三步曲分析:
- 明确递归函数的参数和返回值
参数:当前传入节点。
返回值:以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢?
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
代码如下:
// -1 表示已经不是平衡二叉树了,否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)- 明确终止条件
递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
代码如下:
if (node == NULL) {
return 0;
}- 明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是二叉平衡树了。
代码如下:
int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) { // 中
result = -1;
} else {
result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
}
return result;代码精简之后如下:
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);此时递归的函数就已经写出来了,这个递归的函数传入节点指针,返回以该节点为根节点的二叉树的高度,如果不是二叉平衡树,则返回-1。
getHeight整体代码如下:
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}最后本题整体递归代码如下:
class Solution {
public:
// 返回以该节点为根节点的二叉树的高度,如果不是二叉搜索树了则返回-1
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};在104.二叉树的最大深度中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
本题的迭代方式可以先定义一个函数,专门用来求高度。
这个函数通过栈模拟的后序遍历找每一个节点的高度(其实是通过求传入节点为根节点的最大深度来求的高度)
代码如下:
// cur节点的最大深度,就是cur的高度
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // 记录深度
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}然后再用栈来模拟前序遍历,遍历每一个节点的时候,再去判断左右孩子的高度是否符合,代码如下:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { // 判断左右孩子高度是否符合
return false;
}
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return true;
}整体代码如下:
class Solution {
private:
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // 记录深度
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
public:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
return false;
}
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return true;
}
};当然此题用迭代法,其实效率很低,因为没有很好的模拟回溯的过程,所以迭代法有很多重复的计算。
虽然理论上所有的递归都可以用迭代来实现,但是有的场景难度可能比较大。
例如:都知道回溯法其实就是递归,但是很少人用迭代的方式去实现回溯算法!
因为对于回溯算法已经是非常复杂的递归了,如果在用迭代的话,就是自己给自己找麻烦,效率也并不一定高。
通过本题可以了解求二叉树深度 和 二叉树高度的差异,求深度适合用前序遍历,而求高度适合用后序遍历。
本题迭代法其实有点复杂,大家可以有一个思路,也不一定说非要写出来。
但是递归方式是一定要掌握的!
class Solution {
/**
* 递归法
*/
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
if (leftHeight == -1) {
return -1;
}
int rightHeight = getHeight(root.right);
if (rightHeight == -1) {
return -1;
}
// 左右子树高度差大于1,return -1表示已经不是平衡树了
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
class Solution {
/**
* 迭代法,效率较低,计算高度时会重复遍历
* 时间复杂度:O(n^2)
*/
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root!= null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode inNode = stack.peek();
// 右结点为null或已经遍历过
if (inNode.right == null || inNode.right == pre) {
// 比较左右子树的高度差,输出
if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
return false;
}
stack.pop();
pre = inNode;
root = null;// 当前结点下,没有要遍历的结点了
} else {
root = inNode.right;// 右结点还没遍历,遍历右结点
}
}
return true;
}
/**
* 层序遍历,求结点的高度
*/
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
int depth = 0;
while (!deque.isEmpty()) {
int size = deque.size();
depth++;
for (int i = 0; i < size; i++) {
TreeNode poll = deque.poll();
if (poll.left != null) {
deque.offer(poll.left);
}
if (poll.right != null) {
deque.offer(poll.right);
}
}
}
return depth;
}
}
class Solution {
/**
* 优化迭代法,针对暴力迭代法的getHeight方法做优化,利用TreeNode.val来保存当前结点的高度,这样就不会有重复遍历
* 获取高度算法时间复杂度可以降到O(1),总的时间复杂度降为O(n)。
* 时间复杂度:O(n)
*/
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode inNode = stack.peek();
// 右结点为null或已经遍历过
if (inNode.right == null || inNode.right == pre) {
// 输出
if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
return false;
}
stack.pop();
pre = inNode;
root = null;// 当前结点下,没有要遍历的结点了
} else {
root = inNode.right;// 右结点还没遍历,遍历右结点
}
}
return true;
}
/**
* 求结点的高度
*/
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = root.left != null ? root.left.val : 0;
int rightHeight = root.right != null ? root.right.val : 0;
int height = Math.max(leftHeight, rightHeight) + 1;
root.val = height;// 用TreeNode.val来保存当前结点的高度
return height;
}
}递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
if self.get_height(root) != -1:
return True
else:
return False
def get_height(self, root: TreeNode) -> int:
# Base Case
if not root:
return 0
# 左
if (left_height := self.get_height(root.left)) == -1:
return -1
# 右
if (right_height := self.get_height(root.right)) == -1:
return -1
# 中
if abs(left_height - right_height) > 1:
return -1
else:
return 1 + max(left_height, right_height)迭代法:
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
st = []
if not root:
return True
st.append(root)
while st:
node = st.pop() #中
if abs(self.getDepth(node.left) - self.getDepth(node.right)) > 1:
return False
if node.right:
st.append(node.right) #右(空节点不入栈)
if node.left:
st.append(node.left) #左(空节点不入栈)
return True
def getDepth(self, cur):
st = []
if cur:
st.append(cur)
depth = 0
result = 0
while st:
node = st.pop()
if node:
st.append(node) #中
st.append(None)
depth += 1
if node.right: st.append(node.right) #右
if node.left: st.append(node.left) #左
else:
node = st.pop()
depth -= 1
result = max(result, depth)
return resultfunc isBalanced(root *TreeNode) bool {
if root==nil{
return true
}
if !isBalanced(root.Left) || !isBalanced(root.Right){
return false
}
LeftH:=maxdepth(root.Left)+1
RightH:=maxdepth(root.Right)+1
if abs(LeftH-RightH)>1{
return false
}
return true
}
func maxdepth(root *TreeNode)int{
if root==nil{
return 0
}
return max(maxdepth(root.Left),maxdepth(root.Right))+1
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
func abs(a int)int{
if a<0{
return -a
}
return a
}var isBalanced = function(root) {
//还是用递归三部曲 + 后序遍历 左右中 当前左子树右子树高度相差大于1就返回-1
// 1. 确定递归函数参数以及返回值
const getDepth = function(node) {
// 2. 确定递归函数终止条件
if(node === null) return 0;
// 3. 确定单层递归逻辑
let leftDepth = getDepth(node.left); //左子树高度
let rightDepth = getDepth(node.right); //右子树高度
if(leftDepth === -1) return -1;
if(rightDepth === -1) return -1;
if(Math.abs(leftDepth - rightDepth) > 1) {
return -1;
} else {
return 1 + Math.max(leftDepth, rightDepth);
}
}
return !(getDepth(root) === -1);
};递归法:
int getDepth(struct TreeNode* node) {
//如果结点不存在,返回0
if(!node)
return 0;
//求出右子树深度
int rightDepth = getDepth(node->right);
//求出左子树深度
int leftDepth = getDepth(node->left);
//返回左右子树中的较大值+1
return rightDepth > leftDepth ? rightDepth + 1 : leftDepth + 1;
}
bool isBalanced(struct TreeNode* root) {
//递归结束条件为:传入结点为NULL,返回True
if(!root)
return 1;
//求出左右子树的深度
int leftDepth = getDepth(root->left);
int rightDepth = getDepth(root->right);
int diff;
//若左右子树绝对值差距大于1,返回False
if((diff = leftDepth - rightDepth) > 1 || diff < -1)
return 0;
//检查左右子树是否为平衡二叉树
return isBalanced(root->right) && isBalanced(root->left);
}迭代法:
//计算结点深度
int getDepth(struct TreeNode* node) {
//开辟栈空间
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int stackTop = 0;
//若传入结点存在,将其入栈。若不存在,函数直接返回0
if(node)
stack[stackTop++] = node;
int result = 0;
int depth = 0;
//当栈中有元素时,进行迭代遍历
while(stackTop) {
//取出栈顶元素
struct TreeNode* tempNode = stack[--stackTop];
//若栈顶元素非NULL,则将深度+1
if(tempNode) {
depth++;
//将栈顶元素再次入栈,添加NULL表示此结点已被遍历
stack[stackTop++] = tempNode;
stack[stackTop++] = NULL;
//若栈顶元素有左右孩子,则将孩子结点入栈
if(tempNode->left)
stack[stackTop++] = tempNode->left;
if(tempNode->right)
stack[stackTop++] = tempNode->right;
//更新结果
result = result > depth ? result : depth;
}
else {
//若为NULL,则代表当前结点已被遍历,深度-1
tempNode = stack[--stackTop];
depth--;
}
}
return result;
}
bool isBalanced(struct TreeNode* root){
//开辟栈空间
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int stackTop = 0;
//若根节点不存在,返回True
if(!root)
return 1;
//将根节点入栈
stack[stackTop++] = root;
//当栈中有元素时,进行遍历
while(stackTop) {
//将栈顶元素出栈
struct TreeNode* node = stack[--stackTop];
//计算左右子树的深度
int diff = getDepth(node->right) - getDepth(node->left);
//若深度的绝对值大于1,返回False
if(diff > 1 || diff < -1)
return 0;
//如果栈顶结点有左右结点,将左右结点入栈
if(node->left)
stack[stackTop++] = node->left;
if(node->right)
stack[stackTop++] = node->right;
}
//若二叉树遍历结束后没有返回False,则返回True
return 1;
}