forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy pathdnn-normal.md
82 lines (41 loc) · 7.71 KB
/
dnn-normal.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
# 深度神经网络(DNN)的正则化
---
和普通的机器学习算法一样,DNN也会遇到过拟合的问题,需要考虑泛化,这里我们就对DNN的正则化方法做一个总结。
# 1. DNN的L1&L2正则化
想到正则化,我们首先想到的就是L1正则化和L2正则化。L1正则化和L2正则化原理类似,这里重点讲述DNN的L2正则化。
而DNN的L2正则化通常的做法是只针对与线性系数矩阵W,而不针对偏倚系数b。利用我们之前的机器学习的知识,我们很容易可以写出DNN的L2正则化的损失函数。
假如我们的每个样本的损失函数是均方差损失函数,则所有的m个样本的损失函数为:$$J(W,b) = \frac{1}{2m}\sum\limits_{i=1}^{m}||a^L-y||_2^2$$
则加上了L2正则化后的损失函数是:$$J(W,b) =\frac{1}{2m}\sum\limits_{i=1}^{m}||a^L-y||_2^2 + \frac{\lambda}{2m}\sum\limits_{l=2}^L||w||_2^2$$
其中,$$\lambda$$即我们的正则化超参数,实际使用时需要调参。而w为所有权重矩阵W的所有列向量。
如果使用上式的损失函数,进行反向传播算法时,流程和没有正则化的反向传播算法完全一样,区别仅仅在于进行梯度下降法时,W的更新公式。
回想我们在[深度神经网络(DNN)反向传播算法\(BP\)](/dl/introduction/dnn-bp.md)中,W的梯度下降更新公式为:$$W^l = W^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}(a^{x, l-1})^T$$
则加入L2正则化以后,迭代更新公式变成:$$W^l = W^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}(a^{i, l-1})^T -\alpha \lambda W^l$$
注意到上式中的梯度计算中$$\frac{1}{m}$$我忽略了,因为$$\alpha$$是常数,而除以m也是常数,所以等同于用了新常数$$\alpha$$来代替$$\frac{\alpha}{m}$$。进而简化表达式,但是不影响损失算法。
类似的L2正则化方法可以用于交叉熵损失函数或者其他的DNN损失函数,这里就不累述了。
# 2. DNN通过集成学习的思路正则化
除了常见的L1&L2正则化,DNN还可以通过集成学习的思路正则化。在[集成学习原理小结](/ml/integrate.md)中,我们讲到集成学习有Boosting和Bagging两种思路。而DNN可以用Bagging的思路来正则化。常用的机器学习Bagging算法中,随机森林是最流行的。它 通过随机采样构建若干个相互独立的弱决策树学习器,最后采用加权平均法或者投票法决定集成的输出。在DNN中,我们一样使用Bagging的思路。不过和随机森林不同的是,我们这里不是若干个决策树,而是若干个DNN的网络。
首先我们要对原始的m个训练样本进行有放回随机采样,构建N组m个样本的数据集,然后分别用这N组数据集去训练我们的DNN。即采用我们的前向传播算法和反向传播算法得到N个DNN模型的W,b参数组合,最后对N个DNN模型的输出用加权平均法或者投票法决定最终输出。
不过用集成学习Bagging的方法有一个问题,就是我们的DNN模型本来就比较复杂,参数很多。现在又变成了N个DNN模型,这样参数又增加了N倍,从而导致训练这样的网络要花更加多的时间和空间。因此一般N的个数不能太多,比如5-10个就可以了。
# 3. DNN通过dropout 正则化
这里我们再讲一种和Bagging类似但是又不同的正则化方法:Dropout。
所谓的Dropout指的是在用前向传播算法和反向传播算法训练DNN模型时,一批数据迭代时,随机的从全连接DNN网络中去掉一部分隐藏层的神经元。
比如我们本来的DNN模型对应的结构是这样的:
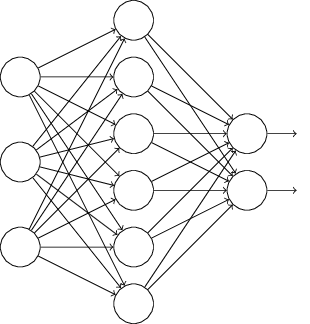
在对训练集中的一批数据进行训练时,我们随机去掉一部分隐藏层的神经元,并用去掉隐藏层的神经元的网络来拟合我们的一批训练数据。如下图,去掉了一半的隐藏层神经元:
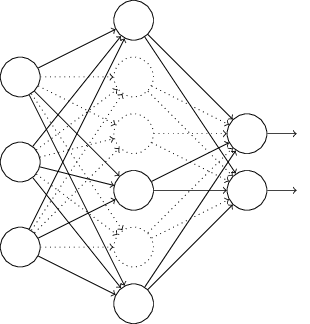
然后用这个去掉隐藏层的神经元的网络来进行一轮迭代,更新所有的W,b。这就是所谓的dropout。
当然,dropout并不意味着这些神经元永远的消失了。在下一批数据迭代前,我们会把DNN模型恢复成最初的全连接模型,然后再用随机的方法去掉部分隐藏层的神经元,接着去迭代更新W,b。当然,这次用随机的方法去掉部分隐藏层后的残缺DNN网络和上次的残缺DNN网络并不相同。
总结下dropout的方法: 每轮梯度下降迭代时,它需要将训练数据分成若干批,然后分批进行迭代,每批数据迭代时,需要将原始的DNN模型随机去掉部分隐藏层的神经元,用残缺的DNN模型来迭代更新W,b。每批数据迭代更新完毕后,要将残缺的DNN模型恢复成原始的DNN模型。
从上面的描述可以看出dropout和Bagging的正则化思路还是很不相同的。dropout模型中的W,b是一套,共享的。所有的残缺DNN迭代时,更新的是同一组W,b;而Bagging正则化时每个DNN模型有自己独有的一套W,b参数,相互之间是独立的。当然他们每次使用基于原始数据集得到的分批的数据集来训练模型,这点是类似的。
使用基于dropout的正则化比基于bagging的正则化简单,这显而易见,当然天下没有免费的午餐,由于dropout会将原始数据分批迭代,因此原始数据集最好较大,否则模型可能会欠拟合。
# 4. DNN通过增强数据集正则化
增强模型泛化能力最好的办法是有更多更多的训练数据,但是在实际应用中,更多的训练数据往往很难得到。有时候我们不得不去自己想办法能无中生有,来增加训练数据集,进而得到让模型泛化能力更强的目的。
对于我们传统的机器学习分类回归方法,增强数据集还是很难的。你无中生有出一组特征输入,却很难知道对应的特征输出是什么。但是对于DNN擅长的领域,比如图像识别,语音识别等则是有办法的。以图像识别领域为例,对于原始的数据集中的图像,我们可以将原始图像稍微的平移或者旋转一点点,则得到了一个新的图像。虽然这是一个新的图像,即样本的特征是新的,但是我们知道对应的特征输出和之前未平移旋转的图像是一样的。
举个例子,下面这个图像,我们的特征输出是5。

我们将原始的图像旋转15度,得到了一副新的图像如下:

我们现在得到了一个新的训练样本,输入特征和之前的训练样本不同,但是特征输出是一样的,我们可以确定这是5.
用类似的思路,我们可以对原始的数据集进行增强,进而得到增强DNN模型的泛化能力的目的。
# 5. 其他DNN正则化方法
DNN的正则化的方法是很多的,还是持续的研究中。在[Deep Learning](http://www.deeplearningbook.org/)这本书中,正则化是洋洋洒洒的一大章。里面提到的其他正则化方法有:Noise Robustness, Adversarial Training,Early Stopping等。如果大家对这些正则化方法感兴趣,可以去阅读[Deep Learning](http://www.deeplearningbook.org/)这本书中的第七章。