forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy pathnegative-sampling.md
126 lines (63 loc) · 8.29 KB
/
negative-sampling.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
# 基于Negative Sampling的模型
---
# 1. Hierarchical Softmax的缺点与改进
在讲基于Negative Sampling的word2vec模型前,我们先看看Hierarchical Softmax的的缺点。的确,使用霍夫曼树来代替传统的神经网络,可以提高模型训练的效率。但是如果我们的训练样本里的中心词w是一个很生僻的词,那么就得在霍夫曼树中辛苦的向下走很久了。能不能不用搞这么复杂的一颗霍夫曼树,将模型变的更加简单呢?
Negative Sampling就是这么一种求解word2vec模型的方法,它摒弃了霍夫曼树,采用了Negative Sampling(负采样)的方法来求解,下面我们就来看看Negative Sampling的求解思路。
# 2. 基于Negative Sampling的模型概述
既然名字叫Negative Sampling(负采样),那么肯定使用了采样的方法。采样的方法有很多种,比如之前讲到的大名鼎鼎的MCMC。我们这里的Negative Sampling采样方法并没有MCMC那么复杂。
比如我们有一个训练样本,中心词是w,它周围上下文共有2c个词,记为context\(w\)。由于这个中心词w,的确和context\(w\)相关存在,因此它是一个真实的正例。通过Negative Sampling采样,我们得到neg个和w不同的中心词$$w_i, i=1,2,..neg$$,这样context\(w\)和$$w_i$$就组成了neg个并不真实存在的负例。利用这一个正例和neg个负例,我们进行二元逻辑回归,得到负采样对应每个词$$w_i$$对应的模型参数$$\theta_{i}$$,和每个词的词向量。
从上面的描述可以看出,Negative Sampling由于没有采用霍夫曼树,每次只是通过采样neg个不同的中心词做负例,就可以训练模型,因此整个过程要比Hierarchical Softmax简单。
不过有两个问题还需要弄明白:1)如果通过一个正例和neg个负例进行二元逻辑回归呢? 2) 如何进行负采样呢?
我们在第三节讨论问题1,在第四节讨论问题2.
# 3. 基于Negative Sampling的模型梯度计算
Negative Sampling也是采用了二元逻辑回归来求解模型参数,通过负采样,我们得到了neg个负例$$(context(w), w_i) i=1,2,..neg$$。为了统一描述,我们将正例定义为$$w_0$$。
在逻辑回归中,我们的正例应该期望满足:$$P(context(w_0), w_i) = \sigma(x_{w_i}^T\theta^{w_i}) ,y_i=1, i=0$$
我们的负例期望满足:$$P(context(w_0), w_i) =1- \sigma(x_i^T\theta^{w_i}), y_i = 0, i=1,2,..neg$$
我们期望可以最大化下式:$$\prod_{i=0}^{neg}P(context(w_0), w_i) = \sigma(x_{w_0}^T\theta^{w_0})\prod_{i=1}^{neg}(1- \sigma(x_{w_i}^T\theta^{w_i}))$$
我们容易写出此时模型的似然函数为:$$\prod_{i=0}^{neg} \sigma(x_{w_i}^T\theta^{w_i})^{y_i}(1- \sigma(x_{w_i}^T\theta^{w_i}))^{1-y_i}$$
此时对应的对数似然函数为:$$L = \sum\limits_{i=0}^{neg}y_i log(\sigma(x_{w_i}^T\theta^{w_i})) + (1-y_i) log(1- \sigma(x_{w_i}^T\theta^{w_i}))$$
和Hierarchical Softmax类似,我们采用随机梯度上升法,仅仅每次只用一个样本更新梯度,来进行迭代更新得到我们需要的$$x_{w_i}, \theta^{w_i}, i=0,1,..neg$$, 这里我们需要求出$$x_{w_i}, \theta^{w_i}, i=0,1,..neg$$的梯度。
首先我们计算$$\theta^{w_i}$$的梯度:$$\begin{aligned} \frac{\partial L}{\partial \theta^{w_i} } &= y_i(1- \sigma(x_{w_i}^T\theta^{w_i}))x_{w_i}-(1-y_i)\sigma(x_{w_i}^T\theta^{w_i})x_{w_i} \\ & = (y_i -\sigma(x_{w_i}^T\theta^{w_i})) x_{w_i} \end{aligned}$$
同样的方法,我们可以求出$$x_{w_i}$$的梯度如下:$$\frac{\partial L}{\partial x^{w_i} } = (y_i -\sigma(x_{w_i}^T\theta^{w_i}))\theta^{w_i}$$
有了梯度表达式,我们就可以用梯度上升法进行迭代来一步步的求解我们需要的$$x_{w_i}, \theta^{w_i}, i=0,1,..neg$$。
# 4. Negative Sampling负采样方法
现在我们来看看如何进行负采样,得到neg个负例。word2vec采样的方法并不复杂,如果词汇表的大小为V,那么我们就将一段长度为1的线段分成V份,每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的,高频词对应的线段长,低频词对应的线段短。每个词w的线段长度由下式决定:$$len(w) = \frac{count(w)}{\sum\limits_{u \in vocab} count(u)}$$
在word2vec中,分子和分母都取了3/4次幂如下:$$len(w) = \frac{count(w)^{3/4}}{\sum\limits_{u \in vocab} count(u)^{3/4}}$$
在采样前,我们将这段长度为1的线段划分成M等份,这里M >> V,这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候,我们只需要从M个位置中采样出neg个位置就行,此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。
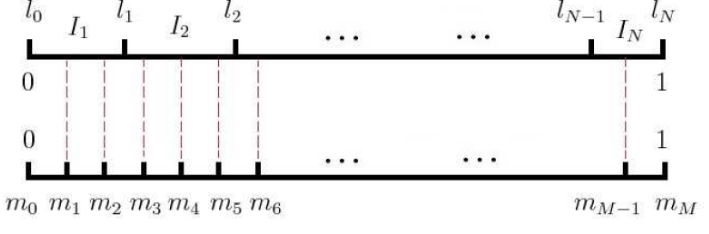
在word2vec中,M取值默认为10^8。
# 5. 基于Negative Sampling的CBOW模型
有了上面Negative Sampling负采样的方法和逻辑回归求解模型参数的方法,我们就可以总结出基于Negative Sampling的CBOW模型算法流程了。梯度迭代过程使用了随机梯度上升法:
输入:基于CBOW的语料训练样本,词向量的维度大小M,CBOW的上下文大小2c,步长$$\eta$$, 负采样的个数neg
输出:词汇表每个词对应的模型参数$$\theta$$,所有的词向量$$x_w$$
1. 随机初始化所有的模型参数$$\theta$$,所有的词向量w
2. 对于每个训练样本$$(context(w_0), w_0)$$,负采样出neg个负例中心词$$w_i, i=1,2,...neg$$
3. 进行梯度上升迭代过程,对于训练集中的每一个样本$$(context(w_0), w_0,w_1,...w_{neg})$$做如下处理:
a\) e=0, 计算$$x_{w_0}= \frac{1}{2c}\sum\limits_{i=1}^{2c}x_i$$
b\) for i= 0 to neg, 计算:$$f = \sigma(x_{w_i}^T\theta^{w_i})$$
$$g = (y_i-f)\eta$$
$$e = e + g\theta^{w_i}$$
$$\theta^{w_i}= \theta^{w_i} + gx_{w_i}$$
c\) 对于context\(w\)中的每一个词向量$$x_j$$\(共2c个\)进行更新:$$x_j = x_j + e$$
d\) 如果梯度收敛,则结束梯度迭代,否则回到步骤3继续迭代。
# 6. 基于Negative Sampling的Skip-Gram模型
有了上一节CBOW的基础和上一篇基于Hierarchical Softmax的Skip-Gram模型基础,我们也可以总结出基于Negative Sampling的Skip-Gram模型算法流程了。梯度迭代过程使用了随机梯度上升法:
输入:基于Skip-Gram的语料训练样本,词向量的维度大小M,Skip-Gram的上下文大小2c,步长$$\eta$$, , 负采样的个数neg。
输出:词汇表每个词对应的模型参数$$\theta$$,所有的词向量$$x_w$$
1. 随机初始化所有的模型参数$$\theta$$,所有的词向量w
2. 对于每个训练样本$$(context(w_0), w_0)$$,负采样出neg个负例中心词$$w_i, i=1,2,...neg$$
3. 进行梯度上升迭代过程,对于训练集中的每一个样本$$(context(w_0), w_0,w_1,...w_{neg})$$做如下处理:
a\) for i =1 to 2c:
i\) e=0
ii\) for i= 0 to neg, 计算:$$f = \sigma(x_{w_i}^T\theta^{w_i})$$
$$g = (y_i-f)\eta$$
$$e = e + g\theta^{w_i}$$
$$\theta^{w_i}= \theta^{w_i} + gx_{w_i}$$
iii\) 对于context\(w\)中的每一个词向量$$x_j$$\(共2c个\)进行更新:$$x_j = x_j + e$$
b\)如果梯度收敛,则结束梯度迭代,算法结束,否则回到步骤a继续迭代。
# 7. Negative Sampling的模型源码和算法的对应
这里给出上面算法和[word2vec源码](https://github.com/tmikolov/word2vec/blob/master/word2vec.c)中的变量对应关系。
在源代码中,基于Negative Sampling的CBOW模型算法在464-494行,基于Hierarchical Softmax的Skip-Gram的模型算法在520-542行。大家可以对着源代码再深入研究下算法。
在源代码中,neule对应我们上面的e, syn0对应我们的$$x_w, syn1neg$$对应我们的$$\theta^{w_i}, layer1_size$$对应词向量的维度,window对应我们的c。negative对应我们的neg, $$table_size$$对应我们负采样中的划分数M。
另外,vocab\[word\].code\[d\]指的是,当前单词word的,第d个编码,编码不含Root结点。vocab\[word\].point\[d\]指的是,当前单词word,第d个编码下,前置的结点。这些和基于Hierarchical Softmax的是一样的。
以上就是基于Negative Sampling的word2vec模型,希望可以帮到大家,后面会讲解用gensim的python版word2vec来使用word2vec解决实际问题。