forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy pathpca.md
170 lines (85 loc) · 13.3 KB
/
pca.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
# 主成分分析(PCA)原理
---
在高维数据处理中,为了简化计算量以及储存空间,需要对这些高维数据进行一定程度上的降维,并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。
PCA:principal component analysis ,主成分分析
ICA :Independent component analysis,独立成分分析
PCA,ICA都是统计理论当中的概念,在机器学习当中应用很广,比如图像,语音,通信的分析处理。
从线性代数的角度去理解,PCA和ICA都是要找到一组基,这组基张成一个特征空间,数据的处理就都需要映射到新空间中去。
两者常用于机器学习中提取特征后的降维操作
PCA是找出信号当中的不相关部分\(正交性),对应二阶统计量分析。PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值\(SVD\)分解去实现。特征值分解也有很多的局限,比如说变换的矩阵必须是方阵,SVD没有这个限制。
PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量,我们在讲一个东西的稳定性的时候,往往说要减小方差,如果一个模型的方差很大,那就说明模型不稳定了。但是对于我们用于机器学习的数据(主要是训练数据),方差大才有意义,不然输入的数据都是同一个点,那方差就为0了,这样输入的多个数据就等同于一个数据了。

主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA,下面我们就对PCA的原理做一个总结。
# 1. PCA的思想
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。具体的,假如我们的数据集是n维的,共有m个数据$$(x^{(1)},x^{(2)},...,x^{(m)})$$。我们希望将这m个数据的维度从n维降到n'维,希望这m个n'维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n'维肯定会有损失,但是我们希望损失尽可能的小。那么如何让这n'维的数据尽可能表示原来的数据呢?
我们先看看最简单的情况,也就是n=2,n'=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向,它可以代表这两个维度的数据。图中列了两个向量方向,$$u_1$$和$$u_2$$,那么哪个向量可以更好的代表原始数据集呢?从直观上也可以看出,$$u_1$$比$$u_2$$好。
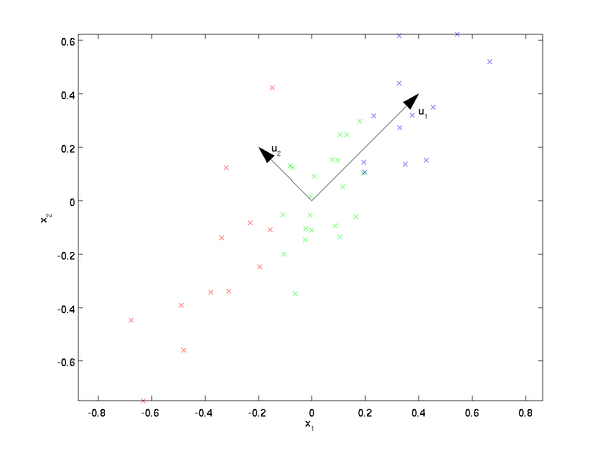
为什么$$u_1$$比$$u_2$$好呢?可以有两种解释,第一种解释是样本点到这个直线的距离足够近,第二种解释是样本点在这个直线上的投影能尽可能的分开。
假如我们把n'从1维推广到任意维,则我们的希望降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们可以得到PCA的两种等价推导。
# 2. PCA的推导:基于小于投影距离
我们首先看第一种解释的推导,即样本点到这个超平面的距离足够近。
假设m个n维数据$$(x^{(1)}, x^{(2)},...,x^{(m)})$$都已经进行了标准化,即$$\sum\limits_{i=1}^{m}x^{(i)}=0$$。经过投影变换后得到的新坐标系为$$\{w_1,w_2,...,w_n\}$$,其中w是标准正交基,即$$||w||_2=1, w_i^Tw_j=0$$。
如果我们将数据从n维降到n'维,即丢弃新坐标系中的部分坐标,则新的坐标系为$$\{w_1,w_2,...,w_{n'}\}$$,样本点$$x^{(i)}$$在n'维坐标系中的投影为:$$z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})$$.其中,$$z_j^{(i)} = w_j^Tx^{(i)}$$是$$x^{(i)}$$在低维坐标系里第j维的坐标。
如果我们用$$z^{(i)}$$来恢复原始数据$$x^{(i)}$$,则得到的恢复数据$$\overline{x}^{(i)} = \sum\limits_{j=1}^{n'}z_j^{(i)}w_j = Wz^{(i)}$$,其中,W为标准正交基组成的矩阵。
现在我们考虑整个样本集,我们希望所有的样本到这个超平面的距离足够近,即最小化下式:$$\sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2$$
将这个式子进行整理,可以得到:
$$\begin{aligned} \sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 & = \sum\limits_{i=1}^{m}|| Wz^{(i)} - x^{(i)}||_2^2 \\& = \sum\limits_{i=1}^{m}(Wz^{(i)})^T(Wz^{(i)}) - 2\sum\limits_{i=1}^{m}(Wz^{(i)})^Tx^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}W^Tx^{(i)} +\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}z^{(i)}+\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} = - \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr(W^T(\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T})W) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} = -tr( W^TXX^TW) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \end{aligned}$$
其中第(1)步用到了$$\overline{x}^{(i)}=Wz^{(i)}$$,第二步用到了平方和展开,第(3)步用到了矩阵转置公式$$(AB)^T =B^TA^T$$和$$W^TW=I$$,第(4)步用到了$$z^{(i)}=W^Tx^{(i)}$$,第(5)步合并同类项,第(6)步用到了$$z^{(i)}=W^Tx^{(i)}$$和矩阵的迹,第7步将代数和表达为矩阵形式。
注意到$$\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}$$是数据集的协方差矩阵,W的每一个向量$$w_j$$是标准正交基。而$$\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}$$是一个常量。最小化上式等价于:
$$
arg min-tr( W^TXX^TW)
$$
$$
s.t. W^TW=I
$$
这个最小化不难,直接观察也可以发现最小值对应的W由协方差矩阵$$XX^T$$最大的n'个特征值对应的特征向量组成。当然用数学推导也很容易。利用拉格朗日函数可以得到$$J(W) = -tr( W^TXX^TW) + \lambda(W^TW-I)$$
对W求导有$$-XX^TW+\lambda W=0$$, 整理下即为:$$XX^TW=\lambda W$$
这样可以更清楚的看出,W为$$XX^T$$的n'个特征向量组成的矩阵,而$$\lambda$$为$$XX^T$$的特征值。当我们将数据集从n维降到n'维时,需要找到最大的n'个特征值对应的特征向量。这n'个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集,我们只需要用$$z^{(i)}=W^Tx^{(i)}$$,就可以把原始数据集降维到最小投影距离的n'维数据集。
如果你熟悉谱聚类的优化过程,就会发现和PCA的非常类似,只不过谱聚类是求前k个最小的特征值对应的特征向量,而PCA是求前k个最大的特征值对应的特征向量。
# 3. PCA的推导:基于最大投影方差
现在我们再来看看基于最大投影方差的推导。
假设m个n维数据$$(x^{(1)}, x^{(2)},...,x^{(m)})$$都已经进行了标准化,即$$\sum\limits_{i=1}^{m}x^{(i)}=0$$。经过投影变换后得到的新坐标系为$$\{w_1,w_2,...,w_n\}$$,其中w是标准正交基,即$$||w||_2=1, w_i^Tw_j=0$$。
如果我们将数据从n维降到n'维,即丢弃新坐标系中的部分坐标,则新的坐标系为$$\{w_1,w_2,...,w_{n'}\}$$,样本点$$x^{(i)}$$在n'维坐标系中的投影为:$$z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})$$.其中,$$z_j^{(i)} = w_j^Tx^{(i)}$$是$$x^{(i)}$$在低维坐标系里第j维的坐标。
对于任意一个样本$$x^{(i)}$$,在新的坐标系中的投影为$$W^Tx^{(i)}$$,在新坐标系中的投影方差为$$W^Tx^{(i)}x^{(i)T}W$$,要使所有的样本的投影方差和最大,也就是最大化$$\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W$$,即:$$argmax \;\;tr( W^TXX^TW) \;\;s.t. W^TW=I$$
观察第二节的基于最小投影距离的优化目标,可以发现完全一样,只是一个是加负号的最小化,一个是最大化。
利用拉格朗日函数可以得到$$J(W) = tr( W^TXX^TW) + \lambda(W^TW-I)$$
对W求导有$$XX^TW+\lambda W=0$$, 整理下即为:$$XX^TW=(-\lambda)W$$
和上面一样可以看出,W为$$XX^T$$的n'个特征向量组成的矩阵,而$$-\lambda$$为$$XX^T$$的特征值。当我们将数据集从n维降到n'维时,需要找到最大的n'个特征值对应的特征向量。这n'个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集,我们只需要用$$z^{(i)}=W^Tx^{(i)}$$,就可以把原始数据集降维到最小投影距离的n'维数据集。
# 4. PCA算法流程
从上面两节我们可以看出,求样本$$x^{(i)}$$的n'维的主成分其实就是求样本集的协方差矩阵$$XX^T$$的前n'个特征值对应特征向量矩阵W,然后对于每个样本$$x^{(i)}$$,做如下变换$$z^{(i)}=W^Tx^{(i)}$$,即达到降维的PCA目的。
下面我们看看具体的算法流程。
输入:n维样本集$$D=(x^{(1)}, x^{(2)},...,x^{(m)})$$,要降维到的维数n'.
输出:降维后的样本集D'
1\) 对所有的样本进行中心化:$$x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$$
2\) 计算样本的协方差矩阵$$XX^T$$
3\) 对矩阵$$XX^T$$进行特征值分解
4)取出最大的n'个特征值对应的特征向量$$(w_1,w_2,...,w_{n'})$$, 将所有的特征向量标准化后,组成特征向量矩阵W。
5)对样本集中的每一个样本$$x^{(i)}$$,转化为新的样本$$z^{(i)}=W^Tx^{(i)}$$
6\) 得到输出样本集$$D' =(z^{(1)}, z^{(2)},...,z^{(m)})$$
有时候,我们不指定降维后的n'的值,而是换种方式,指定一个降维到的主成分比重阈值t。这个阈值t在(0,1\]之间。假如我们的n个特征值为$$\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n$$,则n'可以通过下式得到:$$\frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq t$$
# 5. PCA实例
下面举一个简单的例子,说明PCA的过程。
假设我们的数据集有10个二维数据\(2.5,2.4\), \(0.5,0.7\), \(2.2,2.9\), \(1.9,2.2\), \(3.1,3.0\), \(2.3, 2.7\), \(2, 1.6\), \(1, 1.1\), \(1.5, 1.6\), \(1.1, 0.9\),需要用PCA降到1维特征。
首先我们对样本中心化,这里样本的均值为\(1.81, 1.91\),所有的样本减去这个均值后,即中心化后的数据集为\(0.69, 0.49\), \(-1.31, -1.21\), \(0.39, 0.99\), \(0.09, 0.29\), \(1.29, 1.09\), \(0.49, 0.79\), \(0.19, -0.31\), \(-0.81, -0.81\), \(-0.31, -0.31\), \(-0.71, -1.01\)。
现在我们开始求样本的协方差矩阵,由于我们是二维的,则协方差矩阵为:
$$\mathbf{XX^T} = \left( \begin{array}{ccc} cov(x_1,x_1) & cov(x_1,x_2)\\ cov(x_2,x_1) & cov(x_2,x_2) \end{array} \right)$$
对于我们的数据,求出协方差矩阵为:
$$\mathbf{XX^T} = \left( \begin{array}{ccc} 0.616555556 & 0.615444444\\ 0.615444444 & 0.716555556 \end{array} \right)$$
求出特征值为(0.490833989, 1.28402771),对应的特征向量分别为:$$(0.735178656, 0.677873399)^T\;\; (-0.677873399, -0.735178656)^T$$,由于最大的k=1个特征值为1.28402771,对于的k=1个特征向量为$$(-0.677873399, -0.735178656)^T$$. 则我们的$$W=(-0.677873399, -0.735178656)^T$$
我们对所有的数据集进行投影$$z^{(i)}=W^Tx^{(i)}$$,得到PCA降维后的10个一维数据集为:\(-0.827970186, 1.77758033, -0.992197494, -0.274210416, -1.67580142, -0.912949103, 0.0991094375, 1.14457216, 0.438046137, 1.22382056\)
# 6. 核主成分分析KPCA介绍
在上面的PCA算法中,我们假设存在一个线性的超平面,可以让我们对数据进行投影。但是有些时候,数据不是线性的,不能直接进行PCA降维。这里就需要用到和支持向量机一样的核函数的思想,先把数据集从n维映射到线性可分的高维N>n,然后再从N维降维到一个低维度n', 这里的维度之间满足n'<n<N。
使用了核函数的主成分分析一般称之为核主成分分析\(Kernelized PCA, 以下简称KPCA。假设高维空间的数据是由n维空间的数据通过映射$$\phi$$产生。
则对于n维空间的特征分解:$$\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}W=\lambda W$$
映射为:$$\sum\limits_{i=1}^{m}\phi(x^{(i)})\phi(x^{(i)})^TW=\lambda W$$
通过在高维空间进行协方差矩阵的特征值分解,然后用和PCA一样的方法进行降维。一般来说,映射$$\phi$$不用显式的计算,而是在需要计算的时候通过核函数完成。由于KPCA需要核函数的运算,因此它的计算量要比PCA大很多。
# 7. PCA算法总结
这里对PCA算法做一个总结。作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点,出现了很多PCA的变种,比如第六节的为解决非线性降维的KPCA,还有解决内存限制的增量PCA方法Incremental PCA,以及解决稀疏数据降维的PCA方法Sparse PCA等。
PCA算法的主要优点有:
1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
3)计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
1)主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。