在解决海量数据的问题的时候使用的技术,但是注意这里只是从技术角度进行分析,只是一种思想并不代表业界的技术策略。 常用到的算法策略.
- 分治:多层划分、MapReduce
- 排序:快速排序、桶排序、堆排序
- 数据结构:堆、位图、布隆过滤器、倒排索引、二叉树、Trie树、B树,红黑树
- Hash映射:hashMap、simhash、局部敏感哈希
排序:
将一组无序的集合,根据某个给定的条件,将其变成有序的方法就是排序。从这个我给出的不严谨的定义中排序是方法,目的是让原来无序的集合满足条件有序。
这里我们基于海量数据的考虑重新思考排序,不会详述每一种排序方法的原理,主要面向的是如何在海量数据情况下使用排序方法。
常用的排序方法:
插入排序,选择排序,冒泡排序,希尔排序,快速排序,归并排序,堆排序,桶排序,计数排序,基数排序。 下面给出几种排序算法的简单介绍图。
既然有这么多的排序方法,我们可以直接读取数据到内存中直接调用语言中封装好的排序方法即可。但是数据量很大,不能将数据同时读入内存。
这就出现了所有的外排序,我们可以用归并排序的思想来解决这个问题,也可以基于数据范围用"计数排序"的思想来解决。
排序真的很重要吗?我一直相信一句话:没有排序解决不了的问题。这里给出几个需求,例如:
- 取最大的k个数,直接降序排序取前k个即可;
- 推荐、搜索业务,我们也可以直接排序(精度不高)
- 二分查找之前也要求数据有序
在top k中我们用到了一个数据结构堆(有最大堆和最小堆),这里就先介绍一下这个数据结构的性质,基于最大 堆进行介绍。堆是一个完全二叉树,对于任意的节点,我们可以使用数据来表示最大堆,设置下标从0开始, 满足以下性质:
- root > left && root > right. (左右节点存在)
- 根节点:root_index; 左孩子节点:left_index; 右孩子节点:right_index
- left_index = root_index * 2 + 1
- right_index = root_index * 2 + 2
- root_index = (*_index - 1) / 2
在堆的数据结构进行增删改查的过程中,我们始终维护堆的数据结构,定义MaxheapFy(int *A, int i)表示维护第i个 节点满足最大堆的性质,注意这里没有考虑到泛型编程,正常应该提供一个比较方法的函数,让使用者自己设置比较方式。 从下面的伪代码中,我们可以知道对于一个大小为n的堆,维护一次堆的性质,最坏时间为O(logn),但是必须保证 在改变之前,他是满足堆的性质的。
void MaxheapFy(int *A,int i) {
// i 要在A的范围之内,
assert(i >= 0);
assert(i < n) // 堆的大小
l = LEFT(i), r = RIGHT(i); // 得到左右子节点,如果存在
now = i;
// 找到左右孩子的最大值
if(l<=heapsize&&A[l]>A[now]){
now=l;//交换A[l]和A[i],并递归维护下一个当前结点now
}
if(r<=heapsize&&A[r]>A[now]){
now=r;//交换A[l]和A[i],并递归维护下一个当前结点now
}
if(now != i) { // 交换,递归维护
swap(A[i], A[now]);
MaxheapFy(A, now);
}
}
基于上面的这个维护的性质,我们可以直接对于长度为n的数组建立最大堆,我们知道当只有一个元素的时候,一定满足最大堆的性质, 基于这个性质,我们对于长度为n的数组A,从 n / 2向前维护每一个节点的性质,就可以得到最大堆.从下面给出的最大堆 的构建代码,我们可以分析建堆的时间复杂度是O(nlogn).因为每次维护是O(logn),维护n次,(这里计算时间复杂度的时候,忽略常数系数)。
void BuildMaxHeap(int *A,int n){//A[1..n]
heapsize=n;//全局变量,表示最大堆的大小
for(int i=n/2;i>=1;i--){//从n/2..1维护堆中每个节点的最大堆性质:结点的值大于起孩子的值
MaxheapFY(A,i);
}
}
建成最大堆之后,从最大堆的性质我们知道,A[0]一定是最大值,如果要堆A升序排序,就可以swap(A[0], A[n-1]); 继续维护A[0],直到堆中只是一个元素,这就完成了堆排序。从这个思路出发,对于top k问题,我们为什么要维护一个 最小堆呢,因为我们要过滤所有的数据,保证每次弹出一个最小值,之后剩下的k个一定是top k的最大值,但是这k个不一定 有序,如果需要我们可以堆这k进行任何排序,因为我们通过过滤,数据已经很少了,时间复杂度就是从n个中过滤出来k个。 首先任选k个构建最小堆, 时间复杂度O(klogk), 用最小堆过滤n-k个数字,每次维护堆的性质,时间O((n-k)logk). 总的时间复杂度O(klogk + (n-k)logk)。(注意当k多大时,我们不在使用堆的数据结构,这里留给读者计算)。
void HeapSort(int *A,int n){
BuildMaxHeap(A,n);//建立最大堆
for(int i=n;i>=2;i--){
//cout<<A[1]<<" ";
swap(A[1],A[i]);//交互A[1]和A[i],使得A[i]中为当前最大的元素
heapsize--;//堆大小减去1,便于下次操作去掉已经排好序的元素
MaxheapFY(A,1);//此时A[1]不一定满足最大堆的性质,重新维护下标1的最大堆的性质
}
}
快速排序是对冒泡排序的改进。通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
伪代码
int partition(array,left,right){
index = left;
i = left+1, j = right;
while(1) {
while(i<j && array[i]<array[index]) ++i;
while(i<j && array[j]>array[index]) ++i;
if(i>j) break;
else{
swap(array[i],array[j]);
++i; --j;
}
}
swap(array[index], array[j]);
return j
}
// Qsort(array,0,n-1)
void Qsort(array, left, right){
if(left < right) {
mid = partition(array, left, right);
Qsort(array, left, mid-1);
Qsort(array, mid+1, right);
}
}
快速排序在海量数据处理的过程中,一般不会直接使用,因为快速排序在基于内存的排序时,性能很好,是最常用的方法,例如我们对大数据进行划分后,可以对单个小文件应用快速排序。其实应用多还有就是快速排序中的一次划分很重要,比如我们有很多性别{男,女},请将所有的女性放到男性的前面,我们只需要才有划分思想就OK了。
桶排序的工作原理是将数据分装到有限数量的桶里,对每个桶分别进行排序,如果能将数据均匀分配,排序的速度将是很快的。
伪代码
bucket_sort(array):
buckets[10]; // 申请10个桶
for d in array:
index = function(d) // 将d划分到每一个桶中
buckets[index].append(index)
// 对每一个桶分别进行排序
for i in {1...10}:
sort(buckets[i])
// concat所有结果,这里是连接不是归并,
// 我们划分的时候保证buckets[i] < buckets[i+1]
使用提示,如何想到使用计数排序或者在海量数据处理方面使用计数排序的思想呢?如果我们知道所有的数字只出现一次,我们就可以只使用计算排序中的记录函数,将所有存在的值对应的位置设置为1,否则对应为0,扫描整个数组输出位置为1对应的下标即可完成排序。这种思想可以转为位图排序。
我们使用一个位图来表示所有的数据范围,01位串来表示,如果这个数字出现怎对应的位置就是1,否则就是0.例如我们有一个集合S = {1,4,2,3,6,10,7}; 注意到最大值10,用位图表示为1111011001,对应为1的位置表示这个数字存在,否则表示这个数字不存在。
伪代码
// step 1, 初始化为0
for(i = 0; i < n; i++){
bit[i] = 0;
}
// step 2, 读取数据,对应设置为1
for d in all file_read:
bit[d] = 1
// step3, 对应为1的位置写入文件
for(i = 0; i < n; i++) {
if(bit[i] == 1) {
write i to sort_file
}
}
归并排序: 建立在归并操作上的一种排序算法,该方法采用分治法的一个非常典型应用,一般我们都是使用二路归并,就是将数据划分成两部分进行处理,但是注意我们可以是多路归并,不要让二路归并排序限制我们的思想。 从下面的伪代码中,我们可以很容易看到二路归并排序只有两个部分,一个是递归划分,一个是归并操作,这就是我们最长用到的归并排序。但是在海量数据的排序过程中,我们可以使用二路归并,当然我也可以选择多路归并排序。
伪代码:
// 归并
merge(array, left, mid, right):
tmp = new int[right - left + 1] // 申请复制空间
i = left, j = mid+1, k = 0;
while(i <= mid && j <= right) {
if(array[i] < array[j]) tmp[k++] = array[i++];
else tmp[k++] = array[j++];
}
// 处理尾部,可能会有一部分没有处理结束
while(i <= mid) tmp[k++] = array[i++];
while(j <= right) tmp[k++] = array[j++];
// copy回到原来的数据, tmp -> array
copy(array[left, right], tmp[0,k-1])
// 调用
merge_sort(array, left, right):
if(left < right) {
mid = (left + right) / 2;
merge_sort(array, left, mid);
merge_sort(array, mid+1, right);
// 调用归并函数
merge(arr, left, mid, right);
}
倒排索引是一种索引方法,常用在搜索引擎中,这个数据结构是根据属性值来确定记录的位置。对于一批文档,我们的属性值就是关键字,对应值是包含该属性的文档的ID或者文化的位置。
例如:
构建倒排索引
检索的时候可以根据关键字的交集或者并集进行检索,可以看出,倒排索引就是正向索引的相反。原理其实很简单,可以通过学习或者问题的性质,来发现什么时候使用倒排碎索引,最重要的倒排索引怎么优化,在内存中和文件上如何分配,才能满足快速的检索。倒排索引的构建可以根据自己的业务,决定需要存储什么信息,但是属性值是确定的,对应的集合中可以保留出现的次数等信息。
字典树,Trie树是一种前缀树,我们之前也有介绍过,一般应用在快速查询中,例如搜索提示,当你输入前半部分,会提示后半部分的内容。字典树用一句话表示就是根据字符串的前缀构成的树结构。
格式定义
template<typename T>
struct TreeNode {
int flag; // {1,0}1:表示存在,0:表示不存在
int count: // 表示这个字符串出现的次数
struct TreeNode **childs; // 索引的孩子节点
T value;
};
搜索字典项目的方法为:(来自百度百科)
- 从根结点开始一次搜索;
- 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
- 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
- 迭代过程……
- 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。

- 求top k, 可以用到堆数据结构.
例如我们有100个有序(降序)的数组,现在从这个100个数组中找到最大的k个元素。这就是上述问题的抽象。使用100路归并(后面的归并排序)。 用一个大小为k的最大堆,每次弹出一个最大值,记录是那个队列中的值,直到出现k个数,就结束。这里里面的两个思想,
- 归并,不能处理的大问题,分成多个小问题并行处理,之后归并结果,比如外排序
- 堆,帮助我们找到top k,k要相对n较小。
- 中位数
在一个大小为10GB的文件中有一堆整数,乱序排列,要求找出中位数。内存限制2GB。
这个问题,我们可以使用外排序,并且记录元素的各种,最后得到中位数即可。这里我们使用桶排序的思想。
- 将所有的数据根据前8位进行分桶,最多有255个桶,并且记录每个桶中元素的格式。这里的桶是文件表示。
- 根据划分性质,我们有buckets[i] < buckets[i+1]; count[i]:个数
- 如果sum{count{1,k}} < sum(count{1,n}) / 2 <= sum{count(1,k+1)},得到中位数在k+1个桶中,
+将k+1个桶中读取内存(假设小于2GB,否则要根据次8位进行继续分桶),找到第m个数字,sum{count{1,k}}+m对应的是中位数的下标。
- 基于位图的排序
给你一个文件,里面有n个不重复的正整数,而且每一个数都小于等于n(10^7)。请最多使用1M的内存空间,对这个文件进行排序。
可以使用归并排序,但是时间应该慢,我们这里使用位图排序,$10^7 / 8 = 1.25Mb$, 我们只有1M内存空间,这里可以分成两个读取文件,$(1, 510^6)$和$(510^6, 10^7)$进行分开使用位图,空间占用0.625Mb.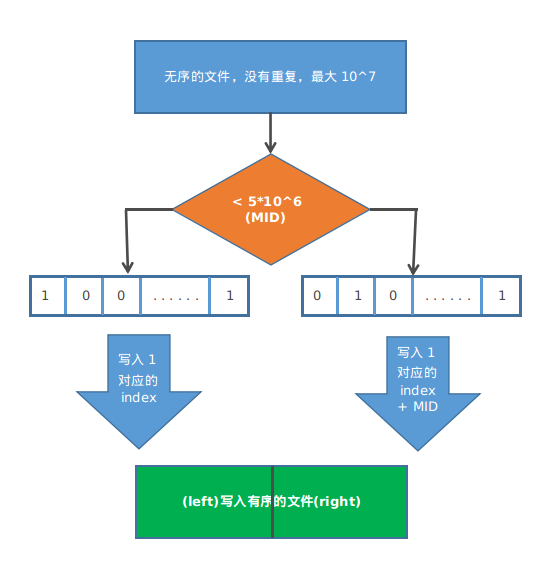
- 大文件排序
海量数据排序,使用归并排序的思想进行排序,例如我们现在有一个5G的数据文件,每一行有一个32位的正整数,现在要求只能使用1G的内存空间,对这个文件排序。 我们有大数据处理的经验都知道,内存放不下,只能将大文件分成几个小文件,这就是划分,之后对每个文件进行排序,最后归并这几个小文件的排序结果,叫做多路归并。上述的过程可以叫做外排序,即借助外部的文件进行排序。
从这个题目出发我们使用之前介绍过的大数据处理技术完成这个排序过程。
- 划分成5个小文件,5G / 1G = 5
- 将单个文件读入内存,进行排序,写入文件
- 使用5路归并,将每个文件作为一路排序,归并最后得到结果

-
串的快速检索
给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。在这道题中,我们可以用数组枚举,用哈希,用字典树,先把熟词建一棵树,然后读入文章进行比较,这种方法效率是比较高的。
-
“串”排序
给定N个互不相同的仅由一个单词构成的英文名,让你将他们按字典序从小到大输出用字典树进行排序,采用数组的方式创建字典树,这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。
-
最长公共前缀
对所有串建立字典树,对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数,于是,问题就转化为当时公共祖先问题。
-
搜索引擎
一个搜索引擎执行的目标就是优化查询的速度:找到某个单词在文档中出现的地方。以前,正向索引开发出来用来存储每个文档的单词的列表,接着掉头来开发了一种反向索引。
正向索引的查询往往满足每个文档有序频繁的全文查询和每个单词在校验文档中的验证这样的查询。实际上,时间、内存、处理器等等资源的限制,技术上正向索引是不能实现的。为了替代正向索引的每个文档的单词列表,能列出每个查询的单词所有所在文档的列表的反向索引数据结构开发了出来。随着反向索引的创建,如今的查询能通过立即的单词标示迅速获取结果(经过随机存储)。随机存储也通常被认为快于顺序存储。
- 数据结构: 构建和使用堆
- 《算法导论》第六章:堆排序
- 《编程之美:面试与算法心得》



