Skip to content

Latest commit

 

History

History
250 lines (197 loc) · 8.24 KB

1035.不相交的线.md

File metadata and controls

250 lines (197 loc) · 8.24 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

1035.不相交的线

力扣题目链接

我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

1035.不相交的线

算法公开课

《代码随想录》算法视频公开课：动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

相信不少录友看到这道题目都没啥思路，我们来逐步分析一下。

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

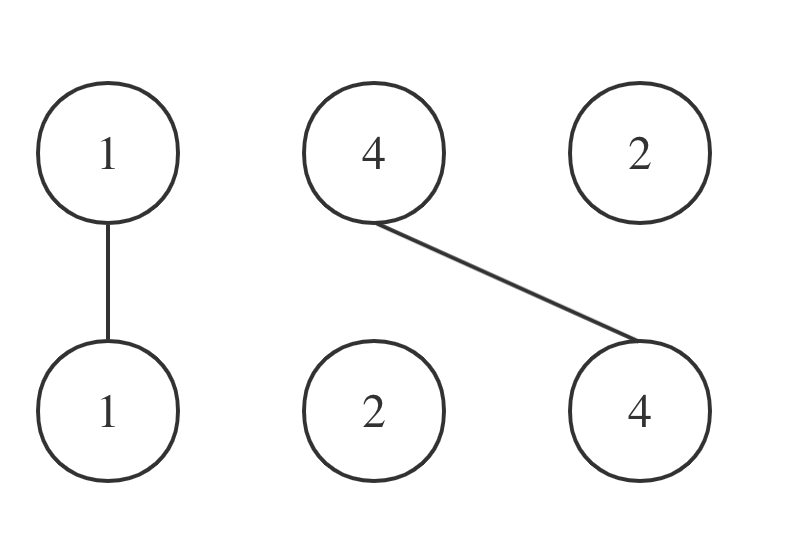
拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

那么本题就和我们刚刚讲过的这道题目动态规划：1143.最长公共子序列就是一样一样的了。

一样到什么程度呢？ 把字符串名字改一下，其他代码都不用改，直接copy过来就行了。

其实本题就是求最长公共子序列的长度，介于我们刚刚讲过动态规划：1143.最长公共子序列，所以本题我就不再做动规五部曲分析了。

如果大家有点遗忘了最长公共子序列，就再看一下这篇：动态规划：1143.最长公共子序列

本题代码如下：

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[A.size()][B.size()];
    }
};
  • 时间复杂度: O(n * m)
  • 空间复杂度: O(n * m)

总结

看到代码大家也可以发现其实就是求两个字符串的最长公共子序列，但如果没有做过1143.最长公共子序列，本题其实还有很有难度的。

这是Carl为什么要先讲1143.最长公共子序列再讲本题，大家会发现一个正确的刷题顺序对算法学习是非常重要的！

这也是Carl做了很多题目（包括ACM和力扣）才总结出来的规律，大家仔细体会一下哈。

其他语言版本

Java：

  class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int[][] dp = new int[len1 + 1][len2 + 1];

        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[len1][len2];
    }
}

Python：

class Solution:
    def maxUncrossedLines(self, A: List[int], B: List[int]) -> int:
        dp = [[0] * (len(B)+1) for _ in range(len(A)+1)]
        for i in range(1, len(A)+1):
            for j in range(1, len(B)+1):
                if A[i-1] == B[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

Go:

func maxUncrossedLines(A []int, B []int) int {
	m, n := len(A), len(B)
	dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }

	for i := 1; i <= len(A); i++ {
		for j := 1; j <= len(B); j++ {
			if (A[i - 1] == B[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1
			} else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
			}
		}
	}
	return dp[m][n]

}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

Rust:

impl Solution {
    pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
        let mut dp = vec![vec![0; nums2.len() + 1]; nums1.len() + 1];
        for (i, num1) in nums1.iter().enumerate() {
            for (j, num2) in nums2.iter().enumerate() {
                if num1 == num2 {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    dp[i + 1][j + 1] = dp[i][j + 1].max(dp[i + 1][j]);
                }
            }
        }
        dp[nums1.len()][nums2.len()]
    }
}

滚动数组

impl Solution {
    pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
        let mut dp = vec![0; nums2.len() + 1];
        for num1 in nums1 {
            let mut prev = 0;
            for (j, &num2) in nums2.iter().enumerate() {
                let temp = dp[j + 1];
                if num1 == num2 {
                    // 使用上一次的状态，防止重复计算
                    dp[j + 1] = prev + 1;
                } else {
                    dp[j + 1] = dp[j + 1].max(dp[j]);
                }
                prev = temp;
            }
        }
        dp[nums2.len()]
    }
}

JavaScript：

const maxUncrossedLines = (nums1, nums2) => {
    // 两个数组长度
    const [m, n] = [nums1.length, nums2.length];
    // 创建dp数组并都初始化为0
    const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            // 根据两种情况更新dp[i][j]
            if (nums1[i - 1] === nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    // 返回dp数组中右下角的元素
    return dp[m][n];
};

TypeScript：

function maxUncrossedLines(nums1: number[], nums2: number[]): number {
    /**
        dp[i][j]: nums1前i-1个，nums2前j-1个，最大连线数
     */
    const length1: number = nums1.length,
        length2: number = nums2.length;
    const dp: number[][] = new Array(length1 + 1).fill(0)
        .map(_ => new Array(length2 + 1).fill(0));
    for (let i = 1; i <= length1; i++) {
        for (let j = 1; j <= length2; j++) {
            if (nums1[i - 1] === nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[length1][length2];
};