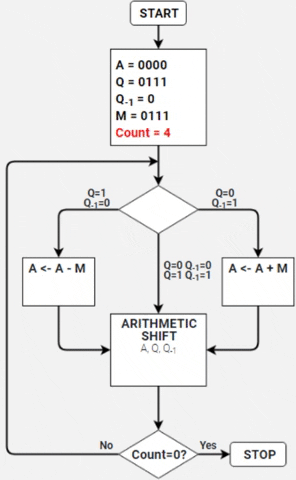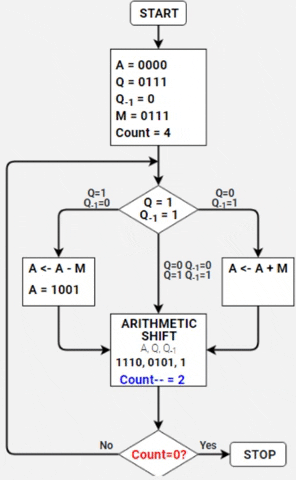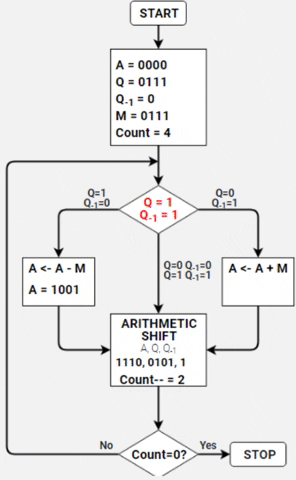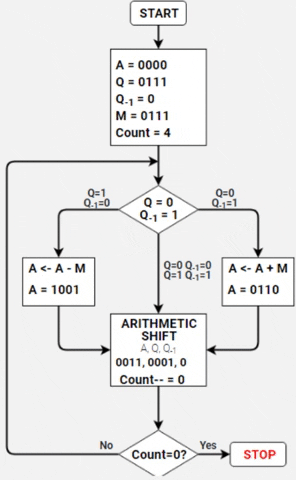
O algoritmo de booth é um algoritmo de multiplicação que permite multiplicar dois inteiros binários com sinal em complemento de 2.
OBS: O algoritmo está disponível para o uso no Git pages.
- Insira nos campos de
inputsos valores e em seguida informe se são valores decimais ou binários, em seguida clique no botãoSend; - Clique no botão
Stepspara ver passo a passo o flowchart do Algoritmo e a tabela; - Use o botão
Resetpara limpar o flowchart e a tabela.
- Converter os valores M (multiplicando) e Q (multiplicador) para binário;
- Se o número informado for menor que 0, usa-se o método complemento de dois;
- Criar um contador com a quantidade de bits do número Q;
- Setar os valores de A e Q-1 para 0;
- Realizar o comparativo entre o último bit de Q com o de Q-1;
- Se Q=1 e Q-1=0, realiza a subtração de A por M e assume este novo valor para A (A <- A -M);
- Se Q=0 e Q-1=1, realiza a soma de A por M e assume este novo valor para A (A <- A + M);
- Se Q=Q-1, não é necessário nenhum passo algébrico, é feito somente o deslocamento;
- Após cada comparativo, realizasse o deslocamento aritmético para a direita e em seguida decrementa o contador.
Multiplicação de (5)10 X (7)10:
- Converter para binário:
- (5)10 = (0101)2;
- (7)10 = (0111)2;
- Criar um contador com a quantidade de bits do multiplicando:
- Count = 4;
- Setar os valores de A e de Q-1 para 0:
- A = 0000;
- Q-1 = 0;
- Comparar o último bit de Q com Q-1:
- Se Q=1 e Q-1=0 -->
A <- A - M; - Se Q=0 e Q-1=1 -->
A <- A + M; - Se Q=Q-1 -->
Nada(nenhum passo algébrico);
- Se Q=1 e Q-1=0 -->
- Realizar o
deslocamento aritmético para a direitae em seguidadecrementar o contador.
Repetir o passo 4° e 5° até o contador ser igual a zero.
Tabela com o passo a passo do exemplo a cima:
| Operação | A | Q | Q-1 | Razão |
|---|---|---|---|---|
| 0000 | 0111 | 0 | Valores Iniciais | |
| A <- A - M | 1011 | 0111 | 0 | 1/4 Ciclo |
| Deslocamento | 1101 | 1011 | 1 | |
| Nada | 1110 | 1011 | 1 | 2/4 Ciclo |
| Deslocamento | 1110 | 1101 | 1 | |
| Nada | 1111 | 1101 | 1 | 3/4 Ciclo |
| Deslocamento | 1111 | 0110 | 1 | |
| A <- A + M | 0100 | 0110 | 1 | 4/4 Ciclo |
| Deslocamento | 0010 | 0011 | 0 |
Resultado: A = 0010 Q = 0011 => (00100011)2 = (35)10
- Faça um fork desse repositório;
- Cria uma branch com a sua feature:
git checkout -b minha-feature; - Faça commit das suas alterações:
git commit -m 'feat: Minha nova feature'; - Faça push para a sua branch:
git push origin minha-feature.
Depois que o merge da sua pull request for feito, você pode deletar a sua branch.
Esse projeto está sob a licença MIT. Veja o arquivo LICENSE para mais detalhes.