Telegram bot for the semantic search of Russian idioms powered by BERT's embeddings approximation, Python, 2021 Try it yourself in tg: @rudiombot
How it works:
TODO list:
- add support for inline mode✅
- add dynamically changing interface✅
- add support for random search of idioms✅
- add history and undo button✅
- add support for searching similar idioms by clicking on them✅
- change language interface depending on user's region code ❌
- calculate other ranking metrics (MAP, NDCG) ❌
- add Paraphrase+ benchmark ❌
- add support for emoji in queries ❌
- add reranking by idiom's popularity ❌
- add daily limits for users ❌
- finetune LaBse on STSb and Paraphrase+ to get better embeddings ❌
First of all, we need to choose the best model for calculating semantic similarity. We can consider BERT architectures. There are two popular approaches, the steady but accurate one and the production-friendly. First one is sentence-pair encoding:
Here two sentences are encoding simultaneously. This means that in order to find similar sentences we have to compute every new prompt with our dataset. It is a huge drawback of such architecture.
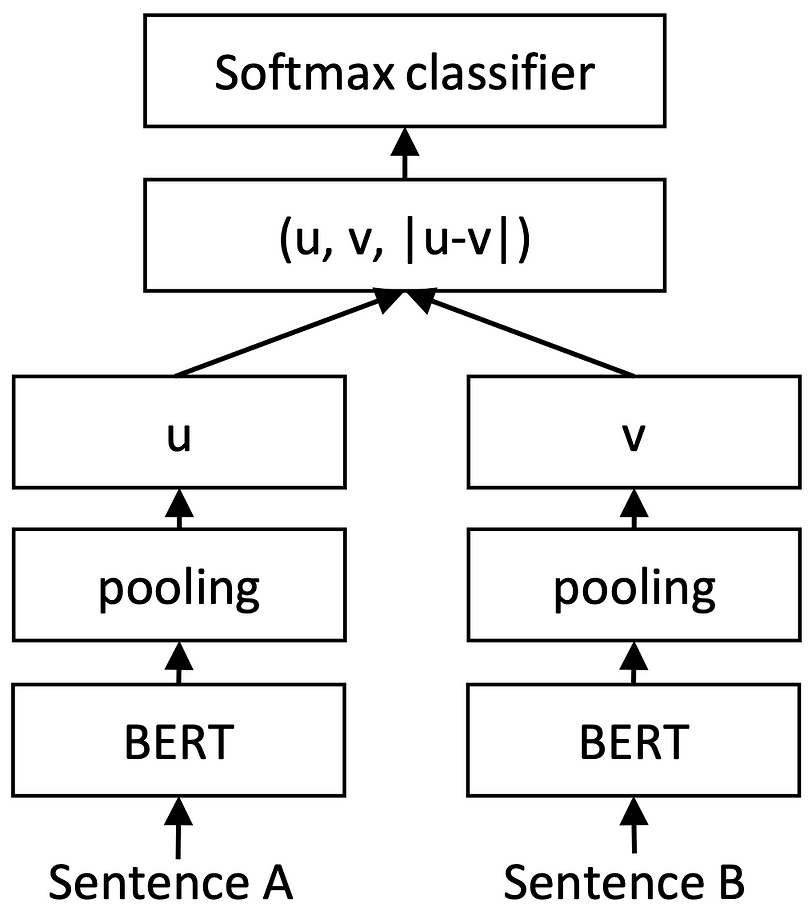
Second one is based on siamese-networks and metric learning:
Such an approach implies that each sentence or document has its own embedding in a learned metric space. Acquired embeddings can be successfully precomputed and stored. To calculate semantic similarity between two sentences we can simply calculate cosine distance. The model's parameters are shared in such a setting during training.
So the second approach is more preferable
We tested accuracies of some pre-trained Russian BERT models on STSb benchmark. We calculate cosine similarities between normalized embeddings (from the class token (CLS) or by averaging encoded tokens (MEAN)):
| MODEL | PARAMS | EMBEDDING SIZE | POOLING TYPE | TRAIN SPEARMAN CORR | TEST SPEARMAN CORR |
|---|---|---|---|---|---|
| cointegrate/rubert-tiny | 12M | 312 | CLS | 0.48472829 | 0.49825618 |
| cointegrate/rubert-tiny | 12M | 312 | MEAN | 0.57088664 | 0.5875781 |
| sberbank-ai/sbert_large_nlu_ru | 335M | 1024 | MEAN | 0.5677551 | 0.5845757 |
| sberbank-ai/ruRoberta-large | 355M | 1024 | MEAN | 0.5847077 | 0.5958275 |
| DeepPavlov/rubert-base-cased-sentence | 180M | 768 | CLS | 0.6538959 | 0.66192624 |
| DeepPavlov/rubert-base-cased-sentence | 180M | 768 | MEAN | 0.6617157 | 0.6686508 |
| sentence-transformers/LaBSE | 470M | 768 | CLS | 0.743942 | 0.7541933 |
| sentence-transformers/LaBSE | 470M | 768 | MEAN | 0.733942 | 0.7364084 |
| cointegrated/LaBSE-en-ru | 127M | 768 | CLS | 0.733942 | 0.7364201 |
| cointegrated/LaBSE-en-ru | 127M | 768 | MEAN | 0.754444 | 0.754402 |
In an ideal case scenario, we would like to use a model with a minimum number of parameters and with high accuracy. However, even if we finetune rubert-tiny on STSb dataset we would get at best only 66% spearman rank correlation.
At the same time, we would like to use smaller embeddings due to the curse of dimensionality when searching among our embeddings. The solution is to find a "good" set of features among these hundreds of dimensions that contains high information. Random search or even worse grid search will require eternity to get such a subset of features. A better method is by using embedded feature selection algorithms via Lasso or L1 Regression. The algorithm for finding a good subset is the following:
- calculate BERT MEAN embeddings E1 and E2 on train and test part of STSb for sentence1 and sentence2 separetely
- calculate element-wise multiplication E1xE2 (one step before summation to get cosine similarity) and element-wise L1 difference abs(E1-E2)
- use acquired numbers as features (so 768+768 = 1526) for Lasso regression as X with intercept and target (similarity score) as y
- find optimal C value via cross-validation on train set
- Argsort weights of the first 768 parameters of the fitted regression model
- Find the best subset of size N on train set via selecting top-N features corresponding to largest signed weights and calculating cosine distances between E1p and E2p
Here are the dependency between Spearman correlation on train set and top-N features of cointegrated/LaBSE-en-ru embeddings:
You can find the full example here:
Google Colab: URL1
Github Gist: URL2
As you can see from the above figure we can achieve a 2.5% boost in performance simply by using a subset of 125 features.
The smallest model (rubert-tiny) perform around 6-10 ms on the CPU. LaBse performs 80-100 ms. Instead of calculating embeddings, we can simply approximate it via some classical ml approaches - TF-IDF. To further reduce the gap between we can use modern tokenization algorithms like WordPiece. The cons of this algorithm:
- better handles OOV (out-of-vocabulary) cases and is used in all BERT and GPT architectures by default.
- smaller vocab size => smaller TfIdf vectors
- may be faster than lemmatization and don't rely on memory-consuming dictionaries
Finally, we can include a special < UNK > token in vocab, otherwise, we will lose information
We can use simple linear regression as a universal approximator trained to predict from given TfIdf vector a BERT's embedding. To achieve better results instead of fitting to highly-correlated embeddings we can predict PCA and then transform it to original embeddings space. So the final architecture can be illustrated as following:
Grey-colored nodes indicate that weights of PCA are not updating during training.
We can also 'contaminate' our training data by purposely dropping some tokens at random or replacing by unknown ones - '< UNK >'. Such an approach provides better results on the fitted model compared to LaBse embeddings:
| MODEL | Params | P@1 | P@3 | P@5 | P@10 | Speed |
|---|---|---|---|---|---|---|
| ApproximateBERT | 1M | 75.47 | 84.82 | 86.88 | 88.35 | 125 us* |
| cointegrated/LaBSE-en-ru | 127M | 73.92 | 81.16 | 82.62 | 83.80 | 80 ms |
Such great speedup was acquired by reimplementing TFiDF transformation and using NumPy array multiplications in float64
To find similar idioms we utilize annoy library on 125 embedding's subset from LaBse. On Intel Xeon 2.3 GHz search with embedding calculation takes around 400 us.