Math in JavaScript

Polynomial.js
Fraction.js
Matrix.js
Vector.js
ComplexNumber.js
BigIntType.js
BigIntFractionComplex.js
RNG.js
functions.js

Polynomial.js

WIP

formula for degree 3/4

chainable methods

make polynomial directly/from string/roots
print as string
finding roots
- Newton's method for degree 3 and higher
- formula for degree 2 and lower
create derivative/antiderivative
calculate f(x)
calculate integral with
- antiderivative formula
- set delta x

Scroll UP | TOP

Fraction.js

make fraction directly/from decimal/-string
GCD & decimal to fraction algorithm as public static methods
fraction to
- improper-form
- mixed-form
- decimal
- string
addition/multiplication/subtraction/divition with
- a single integer
- another fraction
raise fraction to nth power
chainable methods

Scroll UP | TOP

Matrix.js

WIP

row to row addition

row to row subtraction

row multiplied by constant

make matrix directly/from string
create identity matrix
print as a formatted string
single number
- muliplication
- divition
matrix
- addition
- subtraction
- multiplication
- divition
matrix inversion (Gauß Bareiss)
chainable methods
row
- move
- delete
col
- delete
check matrix stats

Scroll UP | TOP

Vector.js

WIP

make vector from string

printing to string

1D, 2D or 3D vector
calculate length
calculate angle
- to other vector
- to X, Y, Z - axis
- to XY, YZ, XZ - plane
- to X, Y, Z - axis on XY, YZ, XZ - plane (2D>3D)
static methods DEG to RAD and RAD to DEG conversion
test if finite
test if equal to another vector
convert vector to unit-vector (length 1 same direction)
vector
- addition
- subtraction
- inversion
- scale by constant (multiply number)

Scroll UP | TOP

ComplexNumber.js

WIP

pow (without polar form) better calculation and support for non-integers

pow with complex exponent z↑z

root (any index) without polar form

root with complex index

log of complex numbers (with custom base)

static (precalculated) values
- RegExp for cartesian (a±bi) and polar form (r∠φrad or r∠φ°)
  - ∠ is U+2220 and ° is U+00B0
- 2π ie τ
- π/2
- π/4
- factor to convert from radians to degrees (180/π)
- factor to convert from degrees to radians (π/180)
create new complex numbers
- from (getter) 0, 1, i, e↑i, or i↑i
- from real and imaginary parts (constructor with new and alias without new)
- from length and angle (from positive real axis in radians)
- from angle (from positive real axis in radians) on unit circle
- from the square root of any real number
- from e↑(i*n) where n is a real number
- from n^i where n is a real number (except 0)
- from logarithm with custom base (except 0 and 1) from any real number (except 0)
- from string in format a±bi or r∠φrad (or degrees r∠φ°)
  - ∠ is U+2220 and ° is U+00B0
attributes (non-private)
- real part (JS Number)
- imaginary part (JS Number)
internal methods (non-private)
- calculate greatest common divisor of two positive safe integers ([1..2↑53[)
- round float to nearest integer when closer than float minimum (JS Number.EPSILON*5)
round complex number (real and imaginary part separately) to nearest integer when closer than float minimum (JS Number.EPSILON*5)
- useful for trigonometric functions as they calculate with small numbers and are thereby prone to float precision errors (noted in JSDoc of affected methods)
getter
- absolute value / length / radius
- angle from polar coordinates (from positive real axis in radians)
  - [0,2π[ / undefined
  - safe [0,2π[ / 0
  - small ]-π,π] / undefined
  - small and safe ]-π,π] / 0
- arc length from positive real axis to the complex number in polar coordinates
- sector (arc area) from positive real axis to the complex number in polar coordinates
convert to string in format a±bi or r∠φrad (or degrees r∠φ°)
- ∠ is U+2220 and ° is U+00B0
log current value to console without breaking method chain
- format: ±a + (±b)i ~ r ∠ φ rad (φ°)
  - ∠ is U+2220 and ° is U+00B0
copy values
- from the current to a new complex number (create a copy)
- from another to the current complex number (override)
- from the current to another complex number (reverse override)
check for equality to 0, 1, or another complex number
arithmetic with complex numbers
- negate current complex number (z*(-1) ie -z)
- invert current complex number (z↑(-1) ie 1/z)
- conjugate of current complex number (a+bi → a-bi)
- rotate complex number (counterclockwise) by an angle (from positive real axis in radians)
- scale angle by a scaler (real number)
- addition with a real number or another complex number
- subtraction with a real number or another complex number
- multiplication with a real number or another complex number
- division with a real number or another complex number
- raising to nth power
  - with kartesian form (currently only safe integers ]-2↑53..2↑53[)
  - with polar form (lower precision but faster and not limited to integers)
- square root ("positive" solution to z↑2)

nth root (currently only safe integers ]-2↑53..2↑53[)

gives a generator that creates all complex solutions to z↑n
ordered counterclockwise from positive real axis
assume first entry is the "positive" root ie. principal root

new ComplexNumber(2,0).pow(-4).roots(-4).next().value?.roundEpsilon().toString()??"no root";
//=> "2+0i"
[...new ComplexNumber(2,0).pow(-4).roots(-4)].map(v=>v.roundEpsilon().toString());
//=> ["2+0i", "0+2i", "-2+0i", "0-2i"]

the class and its prototype are immutable!

import dynamically

const { ComplexNumber } = await import("./ComplexNumber.js");

import in node.js

const { ComplexNumber } = require("./ComplexNumber.js");
// or in modules ↓
import { ComplexNumber } from "./ComplexNumber.js";

import in html:

<script src="./ComplexNumber.js"></script>

Scroll UP | TOP

BigIntType.js

WIP

custom PRNG for randomInt()

BigIntType as type for bitshift methods

new special case for internal division algorithm

arbitrary precision integer using JS's Uint8Array (unsigned 8-bit integer array) human "readable" code with lots of documentation (js-doc & some comments) and descriptive error throws

BigIntType online calculator WIP

adjustable limit MAX_SIZE:Number (Range 1 to 67108864 / 64MiB) (software max is [8PiB-1] - which could be extended to [16PiB-2] using Uint16Array - or even [32PiB-4] using Uint32Array and BigInt)
internal values: sign:Boolean / digits:Uint8Array (base 256 digits) / length:Number (length of digit-array)
during JS type coercion, it converts to BigInt by default or in the context of numbers and to (base 16) String when used in the context of strings
conversions to toBigInt() / ToNumber() / ToString(base)
can be created from, and converted to, different bases
encode toURL() / fromURL()
comparisons:
- isOdd() / isEven()
- A === 0 / A === 1 / A === 2
- A < B / A > B / A == B / A === B / A >= B / A <= B
- isSafeInteger() / isFinite() (for checking if its save to convert to Number)
- isPowerOfTwo() / isPowerOfBase() (256)
chainable methods:
- number constants: 0 / 1 / 2 also negative equivalents and Infinity (1 ** 1024) / MAX_VALUE / HelloThere
- logging to console via logConsole(base) format: [timestamp] (byte count) sign digits (base indicator) (text is green on black and in large monospace font if the console supports it)
- copy/setEqual: copy() / reverseCopy(toOtherNumber) / setEqualTo(otherNumber) / swapWith(otherNumber)
- sign: abs() / neg() (-A) / signNum() (+1 / +0 / -1)
- operations:
  - ++A / --A / A += B / A -= B
  - A *= B using karatsubas algorithm / A **= B
  - A /= B with rounding / A %= B with rounding
  - A *= 2 / A /= 2 with rounding
  - A *= (256 ** x) with rounding - (digit-shifts)
  - A **= 2 / A **= 3
- bitwise operations:
  - A >>>= x / A <<= x / A &= B / A |= B / A ^= B / A ~= A
- GCD(A, B)
- mapRange(a, b, a2, b2) with rounding and limit (cap at a2 / b2)
randomInt(min, max) (using Math.random())
↑ (A and B are type BigIntType and x is type Number) ↑

Supported numerical bases

ALL YOUR BASE ARE BELONG TO US

all bases from 2 to 4'294'967'296 (inclusive) are supported for in- and output
- via String, Number, BigInt, Uint8Array, or array of Numbers
- base 1 is only supported for input
supported prefixes
- 0b for base 2 (binary)
- 0o for base 8 (octal)
- 0x for base 16 (hexadecimal)
used characters (as digits in a string)
- up to base 36 (including), 0-9 and A-Z are used as needed
- above 36 only via CSV (comma-separated-values or numbers in this case), where each number corresponds to the numerical value of the digit at that place (in base 10 / with 0-9)
- "braille" is in base 256 but uses braille patterns (U+2800 to U+28FF inclusive) as digit-charset

Supported numerical base names

Wikipedia: Numerical Bases

base	names	base	names
2	`b` / `bin` / `bits` / `binary` / `1bit`	72	`duoseptuagesimal`
3	`ternary` / `trinary`	80	`octogesimal`
4	`q` / `quaternary` / `2bit`	81	`unoctogesimal`
5	`quinary` / `pental`	85	`pentoctogesimal`
6	`senary` / `heximal` / `seximal`	89	`enneaoctogesimal`
7	`septenary`	90	`nonagesimal`
8	`o` / `oct` / `octal` / `3bit`	91	`unnonagesimal`
9	`nonary`	92	`duononagesimal`
10	`d` / `dec` / `decimal` / `denary`	93	`trinonagesimal`
11	`undecimal`	94	`tetranonagesimal`
12	`duodecimal` / `dozenal` / `uncial`	95	`pentanonagesimal`
13	`tridecimal`	96	`hexanonagesimal`
14	`tetradecimal`	97	`septanonagesimal`
15	`pentadecimal`	100	`centesimal`
16	`h` / `hex` / `hexadecimal` / `sexadecimal` / `4bit`	120	`centevigesimal`
17	`heptadecimal`	121	`centeunvigesimal`
18	`octodecimal`	125	`centepentavigesimal`
19	`enneadecimal`	128	`centeoctovigesimal` / `7bit`
20	`vigesimal`	144	`centetetraquadragesimal`
21	`unvigesimal`	169	`centenovemsexagesimal`
22	`duovigesimal`	185	`centepentoctogesimal`
23	`trivigesimal`	196	`centehexanonagesimal`
24	`tetravigesimal`	200	`duocentesimal`
25	`pentavigesimal`	210	`duocentedecimal`
26	`hexavigesimal`	216	`duocentehexidecimal`
27	`heptavigesimal` / `septemvigesimal`	225	`duocentepentavigesimal`
28	`octovigesimal`	256	`duocentehexaquinquagesimal` / `byte` / `8bit`
29	`enneavigesimal`	300	`trecentesimal`
30	`trigesimal`	360	`trecentosexagesimal`
31	`untrigesimal`	512	`9bit`
32	`duotrigesimal` / `5bit`	1024	`10bit`
33	`tritrigesimal`	2048	`11bit`
34	`tetratrigesimal`	4096	`12bit`
35	`pentatrigesimal`	8192	`13bit`
36	`t` / `txt` / `text` / `hexatrigesimal`	16384	`14bit`
37	`heptatrigesimal`	32768	`15bit`
38	`octotrigesimal`	65536	`16bit`
39	`enneatrigesimal`	131072	`17bit`
40	`quadragesimal`	262144	`18bit`
42	`duoquadragesimal`	524288	`19bit`
45	`pentaquadragesimal`	1048576	`20bit`
47	`septaquadragesimal`	2097152	`21bit`
48	`octoquadragesimal`	4194304	`22bit`
49	`enneaquadragesimal`	8388608	`23bit`
50	`quinquagesimal`	16777216	`24bit`
52	`duoquinquagesimal`	33554432	`25bit`
54	`tetraquinquagesimal`	67108864	`26bit`
56	`hexaquinquagesimal`	134217728	`27bit`
57	`heptaquinquagesimal`	268435456	`28bit`
58	`octoquinquagesimal`	536870912	`29bit`
60	`sexagesimal` / `sexagenary`	1073741824	`30bit`
62	`duosexagesimal`	2147483648	`31bit`
64	`tetrasexagesimal` / `6bit`	4294967296	`32bit`

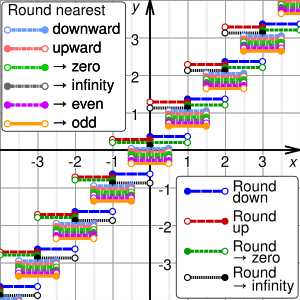
Supported rounding types

name	description	example
`NEAR_DOWN`	round to nearest integer, towards -infinity	+1.5 → +1 +2.5 → +2 −2.5 → −3
`NEAR_UP`	round to nearest integer, towards +infinity	+1.5 → +2 +2.5 → +3 −2.5 → −2
`NEAR_ZERO`	round to nearest integer, towards zero	+1.5 → +1 +2.5 → +2 −2.5 → −2
`NEAR_INF`	round to nearest integer, away from zero	+1.5 → +2 +2.5 → +3 −2.5 → −3
`NEAR_EVEN`	round to nearest even integer	+1.5 → +2 +2.5 → +2 −2.5 → −2
`NEAR_ODD`	round to nearest odd integer	+1.5 → +1 +2.5 → +3 −2.5 → −3
`FLOOR`	round down (towards -infinity)	+1.* → +1 +2.* → +2 −2.* → −3
`CEIL`	round up (towards +infinity)	+1.* → +2 +2.* → +3 −2.* → −2
`TRUNC`	round down (towards zero)	+1.* → +1 +2.* → +2 −2.* → −2
`RAISE`	round up (away from zero)	+1.* → +2 +2.* → +3 −2.* → −3

Supported modulo types

Wikipedia: Modulo

name	description
`ROUND_NEAR_DOWN`	division rounded towards -infinity
`ROUND_NEAR_UP`	division rounded towards +infinity
`ROUND_NEAR_ZERO`	division rounded towards zero
`ROUND_NEAR_INF`	division rounded away from zero
`ROUND_NEAR_EVEN`	division rounded to nearest even integer
`ROUND_NEAR_ODD`	division rounded to nearest odd integer
`FLOOR`	floored division (towards -infinity)
`CEIL`	ceiled division (towards +infinity)
`TRUNC`	truncated division (towards zero)
`RAISE`	raised division (away from zero)
`EUCLID`	euclidean division (positive remainder)

Modulo examples

$\large3\bmod5\implies\frac35=0\frac35=0.6\qquad\text{round up}$

	trunc	floor	euclid	round	ceil	raise
+3 % +5	+3	+3	+3	−2	−2	−2
+3 % −5	+3	−2	+3	−2	+3	−2
−3 % +5	−3	+2	+2	+2	−3	+2
−3 % −5	−3	−3	+2	+2	+2	+2

$\large5\bmod3\implies\frac53=1\frac23=1.\overline6\qquad\text{round up}$

	trunc	floor	euclid	round	ceil	raise
+5 % +3	+2	+2	+2	−1	−1	−1
+5 % −3	+2	−1	+2	−1	+2	−1
−5 % +3	−2	+1	+1	+1	−2	+1
−5 % −3	−2	−2	+1	+1	+1	+1

$\large4\bmod3\implies\frac43=1\frac13=1.\overline3\qquad\text{round down}$

	trunc	floor	euclid	round	ceil	raise
+4 % +3	+1	+1	+1	+1	−2	−2
+4 % −3	+1	−2	+1	+1	+1	−2
−4 % +3	−1	+2	+2	−1	−1	+2
−4 % −3	−1	−1	+2	−1	+2	+2

$\large3\bmod2\implies\frac32=1\frac12=1.5\qquad\text{round down or up }\normalsize\text{(depending on rounding type)}$

	trunc	floor	euclid	round	ceil	raise
+3 % +2	+1	+1	+1	⌊ −1 ⌋ or ⌈ +1 ⌉	−1	−1
+3 % −2	+1	−1	+1	⌊ −1 ⌋ or ⌈ +1 ⌉	+1	−1
−3 % +2	−1	+1	+1	⌊ +1 ⌋ or ⌈ −1 ⌉	−1	+1
−3 % −2	−1	−1	+1	⌊ +1 ⌋ or ⌈ −1 ⌉	+1	+1

$\large3\bmod3\implies\frac33=1\frac03=1.0\qquad\text{round 0 }\normalsize\text{(same as rounding down)}$

	trunc	floor	euclid	round	ceil	raise
+3 % +3	+0	+0	+0	+0	−0	−0
+3 % −3	+0	−0	+0	+0	+0	−0
−3 % +3	−0	+0	+0	−0	−0	+0
−3 % −3	−0	−0	+0	−0	+0	+0

more details/documentation in the file itself via js-docs (/** */) and additional commenting with //~

Scroll UP | TOP

BigIntFractionComplex.js

WIP

idea: BigInt >> Fraction & Infinity >> ComplexNumber

Scroll UP | TOP

RNG.js

RNG stuff

WIP

voronoi noise

perlin noise

Static methods for RNG.noise(x, seed) (non-cryptographic 32bit hash) and RNG.valueNoise2D(x, y, seed).

After instanciating an RNG object (sfc32) with a seed (MurmurHash3) one can get random values via:

val32 gives a random 32bit unsigned integer
val gives a random float 0 to 1 (both inclusive)
dec gives a random decimal 0 to 1 (exclusive 1)
bool gives a random boolean value
range(min, max) gives a random float within the given range (both inclusive)

The RNG state (from an instance) can be saved via state and later restored via RNG.from(state).

Internal but non-private methods:

RNG._hash_(str) creates a 128bit hash via MurmurHash3 (non-cryptographic)
RNG._qLerp_(a, b, t) quintic interpolation used by valueNoise2D

The class and its prototype are immutable!

Import

import dynamically

const { RNG } = await import("./RNG.js");

import in node.js

const { RNG } = require("./RNG.js");
// or in modules ↓
import { RNG } from "./RNG.js";

import in html:
```
<script src="./RNG.js"></script>
```

Test render with valueNoise2D: https://maz01001.github.io/Math-Js/RNG_example.html

Performance test

node.js v16.13.1 on intel i7-10700K

new RNG();new RNG();new RNG();//! warmup
const a=performance.now();
const rng=new RNG();
const b=performance.now();
rng.val32;
const c=performance.now();
{
    const rng=new RNG();
    for(let i=0;i<10000;++i)rng.val32;
}
const d=performance.now();
new RNG().val32;
const e=performance.now();
for(let i=0;i<1000;++i){new RNG("Lorem").val32;new RNG("ipsum").val32;new RNG("dolor").val32;new RNG("sit").val32;new RNG("amet").val32;new RNG("consectetur").val32;new RNG("adipiscing").val32;new RNG("elit").val32;new RNG("Terram").val32;new RNG("mihi").val32;}
const f=performance.now();
for(let i=0;i<10000;++i)new RNG(""+i).val32;
const g=performance.now();
RNG.noise(0x3FA98E75);
const h=performance.now();
for(let i=0;i<1000;++i){RNG.noise(0x3FA98E75);RNG.noise(0x16D9FCA5);RNG.noise(0x1C7590AF);RNG.noise(0x28C6E13D);RNG.noise(0x2CA6DF15);RNG.noise(0x4E0C719F);RNG.noise(0x5237A8B1);RNG.noise(0xD7F3E9AB);RNG.noise(0xF21D5409);RNG.noise(0xF93C5AEB);}
const i=performance.now();
for(let i=0;i<10000;++i)RNG.noise(i);
const j=performance.now();
for(let i=0;i<10000;++i)RNG.valueNoise2D(i,i*0xF47A23);
const k=performance.now();
console.log([
    `                     init new RNG: ${(b-a).toFixed(4).padStart(9)} ms`,//=>    0.0150 ms
    `                            val32: ${(c-b).toFixed(4).padStart(9)} ms`,//=>    0.0285 ms
    `              init + 10'000 val32: ${(d-c).toFixed(4).padStart(9)} ms`,//=>    1.8899 ms
    `                       init val32: ${(e-d).toFixed(4).padStart(9)} ms`,//=>    0.0218 ms
    `             1000 * 10 init val32: ${(f-e).toFixed(4).padStart(9)} ms`,//=>   10.0103 ms
    `                10'000 init val32: ${(g-f).toFixed(4).padStart(9)} ms`,//=>    5.5522 ms
    `                      prime noise: ${(h-g).toFixed(4).padStart(9)} ms`,//=>    0.0781 ms
    `            1000 * 10 prime noise: ${(i-h).toFixed(4).padStart(9)} ms`,//=>    1.7489 ms
    `             10'000 counter noise: ${(j-i).toFixed(4).padStart(9)} ms`,//=>    0.2728 ms
    `10'000 counter+prime valueNoise2D: ${(k-j).toFixed(4).padStart(9)} ms`,//=>    4.4087 ms
    `                            TOTAL: ${(k-a).toFixed(4).padStart(9)} ms`,//=>   24.0262 ms
].join("\n"));

Scroll UP | TOP

functions.js

some useful math functions

also see other-projects/useful.js

mapRange

translate the given number to another range

function mapRange(n: number, a: number, b: number, x: number, y: number, limit?: boolean | undefined): number
mapRange(0.5, 0, 1, 0, 100); //=> 50
mapRange(3, 0, 1, 0, 100); //=> 300
mapRange(3, 0, 1, 0, 100, true); //=> 100

toPercent

calculates the percentage of the given number within the given range

function toPercent(n: number, x: number, y: number): number
toPercent(150, 100, 200); //=> 0.5 = 50%

deg2rad

converts the given angle from DEG to RAD

function deg2rad(deg: number): number

rad2deg

converts the given angle from RAD to DEG

function rad2deg(rad: number): number

gcd

calculates the greatest common divisor of n and m (positive safe integers [1..2↑53[)

function gcd(n: number, m: number): number
gcd(45, 100); //=> 5 → (45/5) / (100/5) → 9/20

dec2frac

converts a decimal number to an improper-fraction (rough estimation)

function dec2frac(dec: number, loop_last?: number | undefined, max_den?: number | undefined, max_iter?: number | undefined): Readonly<{
    a: number;
    b: number;
    c: number;
    i: number;
    r: string;
}>
dec2frac(0.12, 2); //=> { a:0, b:4, c:33, i:0, r:"precision" } → 0+4/33 → 0.121212121212...

padNum

convert number to string with padding
format: [sign] [padded start ' '] [.] [padded end '0'] [e ~]

function padNum(n: number | string, first?: number | undefined, last?: number | undefined): string
padNum("1.23e2", 3, 5); //=> "+  1.23000e2"

euclideanModulo

calculates the modulo of two whole numbers (euclidean division)

$$\large a-\left(\lvert b\rvert\cdot\left\lfloor\dfrac{a}{\lvert b\rvert}\right\rfloor\right)$$

function euclideanModulo(a: number, b: number): number

randomRange

genarates a random number within given range (inclusive)

gets a random number via Math.random() and assumes that this number is in range [0 to (1 - Number.EPSILON)] (inclusive)

function randomRange(min: number, max: number): number

randomRangeInt

genarates a random integer within given range (inclusive)

function randomRangeInt(min: number, max: number): number

divisionWithRest

division with two unsigned numbers

$$\large\dfrac{A}{B}=Q+\dfrac{R}{B}$$

function divisionWithRest(A: number, B: number): readonly [number, number]
divisionWithRest(5, 3); //=> [1, 2] → 1+2/3

also see Math-Js/BigIntType.js : #calcDivRest for a solution with arbitrary-length-integers

randomBools

generate a set amount of random booleans
generator function

function randomBools(amount?: number | undefined): Generator<boolean, any, unknown>
for(const rng of randomBools(3))console.log("%O",rng);

rangeGenerator

creates a generator for given range - iterable
use Array.from() to create a normal number[] array

function rangeGenerator(start: number, end: number, step?: number | undefined, overflow?: boolean | undefined): Generator<number, void, unknown>
for(const odd of rangeGenerator(1, 100, 2))console.log(odd); //~ 1 3 5 .. 97 99

rng32bit

get a function to get random numbers like Math.random but from a given seed
uses MurmurHash3 for seeding and sfc32 for generating 32bit values

function rng32bit(seed?: string | undefined): () => number
rng32bit("seed")();            //=> 3595049765 [0 to 0xFFFFFFFF inclusive]
rng32bit("seed")()/0xFFFFFFFF; //=> 0.8370377509475307 [0.0 to 1.0 inclusive]
rng32bit("seed")()/0x100000000;//=> 0.8370377507526428 [0.0 inclusive to 1.0 exclusive]

valueNoise

calculates value noise for given coordinates
uses quintic interpolation for mixing numbers, and a quick (non-cryptographic) hash function to get random noise from coordinates
the output is allways the same for the same input

function valueNoise(x: number, y: number): number

Example render

I used the following code to render the background on the preview of my r/place overlay script

const size = Object.freeze([1920, 1080]),
    exampleNoise = new ImageData(...size, {colorSpace: "srgb"});
for(let x = 0, y = 0; y < size[1] && x < size[0]; ++x >= size[0] ? (x = 0, y++) : 0){
    const pixel = valueNoise(x * 0.008, y * 0.008) * 127
        + valueNoise(x * 0.016, y * 0.016) * 63.5
        + valueNoise(x * 0.032, y * 0.032) * 31.75
        + valueNoise(x * 0.064, y * 0.064) * 15.875
        + valueNoise(x * 0.128, y * 0.128) * 7.9375;
        //// + valueNoise(x * 0.256, y * 0.256) * 3.96875
        //// + valueNoise(x * 0.512, y * 0.512) * 1.984375;
    exampleNoise.data.set([pixel, pixel, pixel, 0xFF], (y * size[0] + x) * 4);
}
document.body.style.backgroundImage = (() => {
    "use strict";
    const canvas = document.createElement("canvas");
    canvas.width = size[0];
    canvas.height = size[1];
    canvas.getContext("2d")?.putImageData(exampleNoise, 0, 0);
    return `url(${ canvas.toDataURL("image/png") })`;
})();

factorial

calculates the factorial of a non-zero positive integer

must be either number in range [0..18] or bigint

type int = number | bigint
function factorial(n: int): int

// number of possible shuffles of a deck of cards
factorial(52n);//=> 80658175170943878571660636856403766975289505440883277824000000000000n (~ 8e+67)
// highest possible with `number` type
factorial(18); //=>   6402373705728000
factorial(19n);//=> 121645100408832000n

isPrime

calculates if a given number (in safe integer range: ]-2↑53,2↑53[) is prime

function isPrime(x: number): boolean

Performance test

node.js v16.13.1 on intel i7-10700K

const t=[
    performance.now(),isPrime(31),              //=>   0.0472 ms : Prime (warmup)
    performance.now(),isPrime(31),              //=>   0.0024 ms : Prime
    performance.now(),isPrime(331),             //=>   0.0014 ms : Prime
    performance.now(),isPrime(3331),            //=>   0.0013 ms : Prime
    performance.now(),isPrime(33331),           //=>   0.0050 ms : Prime
    performance.now(),isPrime(333331),          //=>   0.0089 ms : Prime
    performance.now(),isPrime(3333331),         //=>   0.0089 ms : Prime
    performance.now(),isPrime(33333331),        //=>   0.0248 ms : Prime
    //~ https://oeis.org/A123568 ↑
    performance.now(),isPrime(6779164939),      //=>   2.4889 ms : Prime
    performance.now(),isPrime(2**52-1),         //=>   1.3814 ms : -----
    performance.now(),isPrime(2**52-47),        //=> 118.1830 ms : Prime
    performance.now(),isPrime(2**53-3155490991),//=> 165.7968 ms : ----- (largest safe prime**2)
    performance.now(),isPrime(2**53-145),       //=> 165.4307 ms : Prime (2nd largest safe prime)
    performance.now(),isPrime(2**53-111),       //=> 166.0785 ms : Prime (largest safe prime)
    performance.now(),isPrime(2**53-94),        //=>   0.0073 ms : ----- (largest safe 2*prime)
    performance.now(),isPrime(2**53-1),         //=>   0.0123 ms : -----
    performance.now()
];
//@ts-ignore t has an even number of entries where every even element is type `number` and every odd `boolean` (impossible to type-doc and/or detect by linter)
for(let i=0;i+1<t.length;i+=2)console.log((t[i+2]-t[i]).toFixed(4).padStart(9),"ms :",t[i+1]?"Prime":"-----");

lastPrime

calculates the next prime number smaller than the given number (in safe integer range: ]-2↑53,2↑53[)

undefined for numbers 2 and smaller that have no previous prime number

function lastPrime(x: number): number|undefined

Performance test

node.js v16.13.1 on intel i7-10700K

const t=[
    performance.now(),lastPrime(2),        //=>   0.0454 ms :        undefined (warmup)
    performance.now(),lastPrime(2),        //=>   0.0019 ms :        undefined
    performance.now(),lastPrime(8),        //=>   0.0018 ms :                7
    performance.now(),lastPrime(32),       //=>   0.0014 ms :               31
    performance.now(),lastPrime(64),       //=>   0.0010 ms :               61
    performance.now(),lastPrime(1024),     //=>   0.0012 ms :             1021
    performance.now(),lastPrime(2**20),    //=>   0.0083 ms :          1048573
    performance.now(),lastPrime(2**30),    //=>   0.2444 ms :       1073741789
    performance.now(),lastPrime(2**40),    //=>   7.2193 ms :    1099511627689
    performance.now(),lastPrime(2**50),    //=>  63.1086 ms : 1125899906842597
    performance.now(),lastPrime(2**53-145),//=> 337.8073 ms : 9007199254740761 (2nd largest safe prime)
    performance.now(),lastPrime(2**53-111),//=> 173.6542 ms : 9007199254740847 (largest safe prime)
    performance.now(),lastPrime(2**53-1),  //=> 195.3127 ms : 9007199254740881 (largest safe integer)
    performance.now()
];
//@ts-ignore t has an even number of entries where every even element is type `number` and every odd `boolean` (impossible to type-doc and/or detect by linter)
for(let i=0;i+1<t.length;i+=2)console.log((t[i+2]-t[i]).toFixed(4).padStart(9),"ms :",String(t[i+1]).padStart(16));

nextPrime

calculates the next prime number larger than the given number (in safe integer range: ]-2↑53,2↑53[)

undefined when the next prime number is not a safe integer (>=2↑53)

function nextPrime(x: number): number|undefined

// generate all primes in range [10..100] (via iterator/generator function)
console.log(...(function*(s,e){for(let p=nextPrime(s-1)??NaN;p<=e;p=nextPrime(p)??NaN)yield p;})(10,100));
//=> 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

Performance test

node.js v16.13.1 on intel i7-10700K

const t=[
    performance.now(),nextPrime(2),        //=>   0.0501 ms :                3 (warmup)
    performance.now(),nextPrime(2),        //=>   0.0019 ms :                3
    performance.now(),nextPrime(8),        //=>   0.0022 ms :               11
    performance.now(),nextPrime(32),       //=>   0.0017 ms :               37
    performance.now(),nextPrime(64),       //=>   0.0012 ms :               67
    performance.now(),nextPrime(1024),     //=>   0.0018 ms :             1031
    performance.now(),nextPrime(2**20),    //=>   0.0097 ms :          1048583
    performance.now(),nextPrime(2**30),    //=>   0.2133 ms :       1073741827
    performance.now(),nextPrime(2**40),    //=>   4.2761 ms :    1099511627791
    performance.now(),nextPrime(2**50),    //=>  78.6495 ms : 1125899906842679
    performance.now(),nextPrime(2**53-145),//=> 174.2993 ms : 9007199254740881 (2nd largest safe prime)
    performance.now(),nextPrime(2**53-111),//=>  22.4187 ms :        undefined (largest safe prime)
    performance.now(),nextPrime(2**53-1),  //=>   0.0056 ms :        undefined (largest safe integer)
    performance.now()
];
//@ts-ignore t has an even number of entries where every even element is type `number` and every odd `boolean` (impossible to type-doc and/or detect by linter)
for(let i=0;i+1<t.length;i+=2)console.log((t[i+2]-t[i]).toFixed(4).padStart(9),"ms :",String(t[i+1]).padStart(16));

factorize

calculates the prime decomposition of the given safe integer (]-2↑53..2↑53[)

prime factors are in ascending order and the list is empty for numbers below 2 (no prime factors)

function factorize(n: number): number[]

Performance test

node.js v16.13.1 on intel i7-10700K

const t=[
    performance.now(),factorize(4),               //=>   0.0494 ms : 2 2 (warmup)
    performance.now(),factorize(4),               //=>   0.0022 ms : 2 2
    performance.now(),factorize(108),             //=>   0.0014 ms : 2 2 3 3 3
    performance.now(),factorize(337500),          //=>   0.0022 ms : 2 2 3 3 3 5 5 5 5 5
    performance.now(),factorize(277945762500),    //=>   0.0049 ms : 2 2 3 3 3 5 5 5 5 5 7 7 7 7 7 7 7
    //~ https://oeis.org/A076265 ↑
    performance.now(),factorize(33332),           //=>   0.0079 ms : 2 2 13 641
    performance.now(),factorize(33223575732),     //=>   0.0279 ms : 2 2 3 599 1531 3019
    performance.now(),factorize(277945762499),    //=>   3.5837 ms : 41 6779164939
    performance.now(),factorize(2**53-3155490991),//=> 175.6862 ms : 94906249 94906249  (largest safe prime**2)
    performance.now(),factorize(2**53-111),       //=> 174.6259 ms : 9007199254740881   (largest safe prime)
    performance.now(),factorize(2**53-94),        //=> 121.8000 ms : 2 4503599627370449 (largest safe 2*prime)
    performance.now()
];
//@ts-ignore t has an even number of entries where every even element is type `number` and every odd `number[]` (impossible to type-doc and/or detect by linter)
for(let i=0;i+1<t.length;i+=2)console.log((t[i+2]-t[i]).toFixed(4).padStart(9),"ms :",...t[i+1]);

Scroll UP | TOP

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Repository files navigation

Math in JavaScript

Polynomial.js

Fraction.js

Matrix.js

Vector.js

ComplexNumber.js

BigIntType.js

BigIntFractionComplex.js

RNG.js

functions.js

About

Languages

Name		Name	Last commit message	Last commit date
Latest commit History 239 Commits
BigIntFractionComplex.js		BigIntFractionComplex.js
BigIntType.js		BigIntType.js
ComplexNumber.js		ComplexNumber.js
Fraction.js		Fraction.js
LICENSE		LICENSE
Matrix.js		Matrix.js
Polynomial.js		Polynomial.js
README.md		README.md
RNG.js		RNG.js
RNG_example.html		RNG_example.html
Vector.js		Vector.js
functions.js		functions.js

License

MAZ01001/Math-Js

Folders and files

Latest commit

History

Repository files navigation

Math in JavaScript

About

Topics

Resources

License

Stars

Watchers

Forks

Languages