Лабораторная работа по алгоритмам и структурам данных #1

Задача

Есть целочисленная матрица размером N x M со следующими свойствами:

• В каждой строке числа упорядочены строго по возрастанию
• В каждом столбце числа упорядочены строго по возрастанию

На вход передается целое число. Необходимо определить, присутствует ли оно в матрице и вернуть true, если оно есть, в противном случае - вернуть false.

Пример входных данных и результат работы алгоритма:

Матрица: [[1, 20, 40, 500], [2, 30, 50, 600], [3, 40, 60, 700], [4, 60, 70, 800]]

Число. которое ищем в матрице: 60

Что вернет алгоритм с данными выше: true (число присутствует)

Варианты решения задачи

1) Обход из правого верхнего угла

Начинаем с правого верхнего элемента матрицы
Варианты действий:

• спускаемся вниз, если текущий элемент на позиции меньше, чем искомый
• идем влево, если текущий элемент на позиции больше, чем искомый
• текущий элемент равен искомому, значит искомый элемент присутствует в матрице, завершаем алгоритм

Сложность алгоритма: O(N + M)

2) Бинарный поиск по строкам и столбцам

а). Делаем проход по строкам в цикле и для каждой строки осуществляем бинарный поиск по нахождению искомого элемента в строке. Продолжаем алгоритм, пока искомый элемент не будет найден или будут пройдены все строки, б). Либо делаем аналогичный проход по столбцам и для каждого столбца осуществляем аналогичный бинарный поиск

Сложность алгоритма: а). O(NlogM) б). O(MlogN)

3) Экспоненциальный поиск с лестничной оптимизацией

С первой строки экспоненциальным поиском ищем элемент или индекс наибольшего элемента, меньшего чем искомый. Если элемент не найден, то идем на следующую строку, начиная с найденного индекса.

Сложность алгоритма: а) M(logN - logM + 1)

Графики:

Сравнение линейного, бинарного и экспоненциального алгоритмов

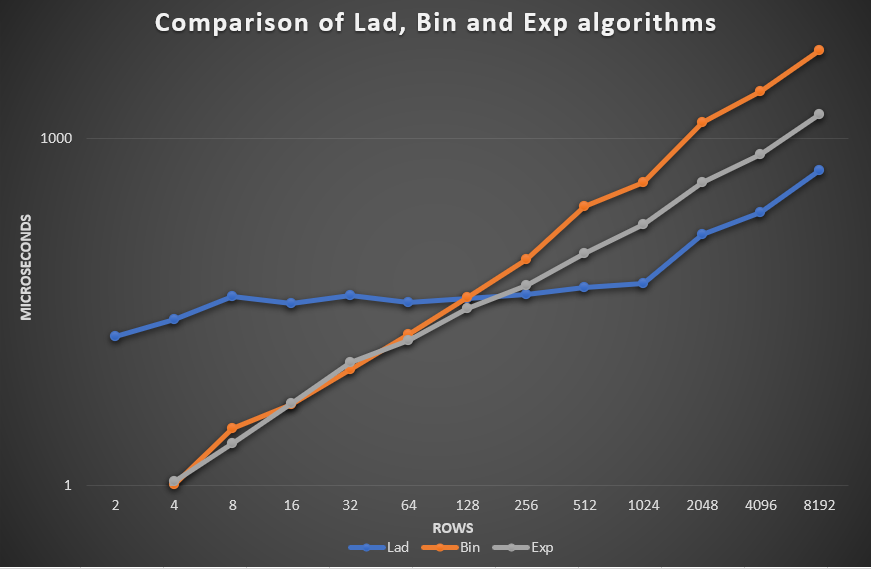
Ремарка: в моей реализации бинарный поиск работает по max(rows, columns), в то время как эспоненциальный поиск работает горизонтально.

В связи с этим, Bin и Exp начинают проигрывать Lad при растягивании матрицы вниз(увеличении M). Лестничная реализация же показала себя максимально стабильно.

Exp быстрее, когда M>N в 2^6(в данном примере) раз и более, то есть, когда количество столбцов доминирует над количеством строк. За счёт умножения на 2 мы быстренько проскакиваем по столбцам, но мы ничего не можем сделать с большим количеством строк.

Bin быстрее, когда M>N или N>M в 2^7 раз и более, то есть, когда между строками и столбцами есть весомая разница.

Преимущество бинарного поиска в том, что мы быстро проскакиваем по max(rows,columns). Но если и rows, и columns принимают большие значения, то быстро проскочить мы может только одно из них.

Lad поиск успешно себя проявляет, когда N/M или M/N <= 2^5, то есть, когда размеры N и M становятся сравнимы. В отличие от Exp и Bin, мы не можем быстро проскочить ни по строкам, ни по столбцам. Мы с линейной скоростью ходим в обе стороны. И если на больших значения строк и столбцов, Exp и Bin проскакивают быстро по столбцам или строкам, а по оставшемуся идут медленно, то ступенчатый алгоритм позволяет сохранять линейную скорость независимо от размеров матрицы.

Сравнение экспонецниального алгоритма на линейной и экспоненциальной генерации данных

Как генерируются данные:

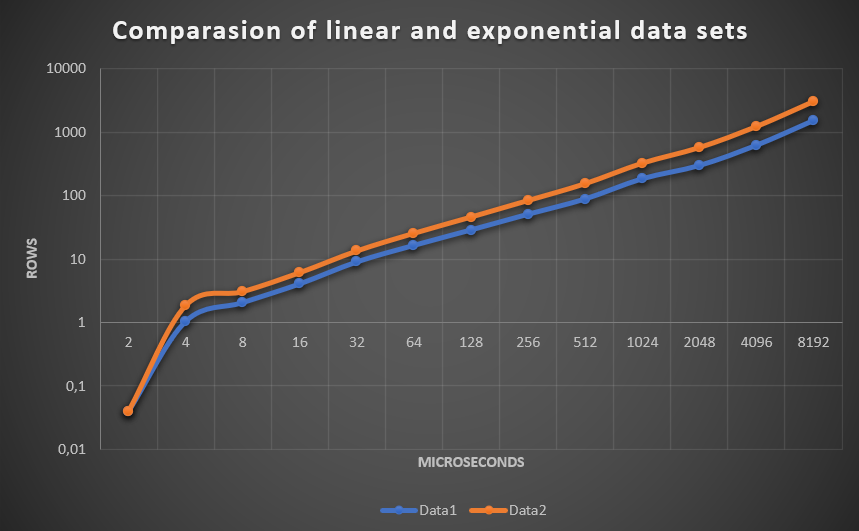
MxN, M <= n, M = 2^x, x = [1..13], N = 2^13

Линейная генерация: A[i][j] = (N / M * i + j) * 2
target = 2N+1

Экспоненциальная генерация: A[i][j] = (N / M * i * j) * 2
target = 16N+1