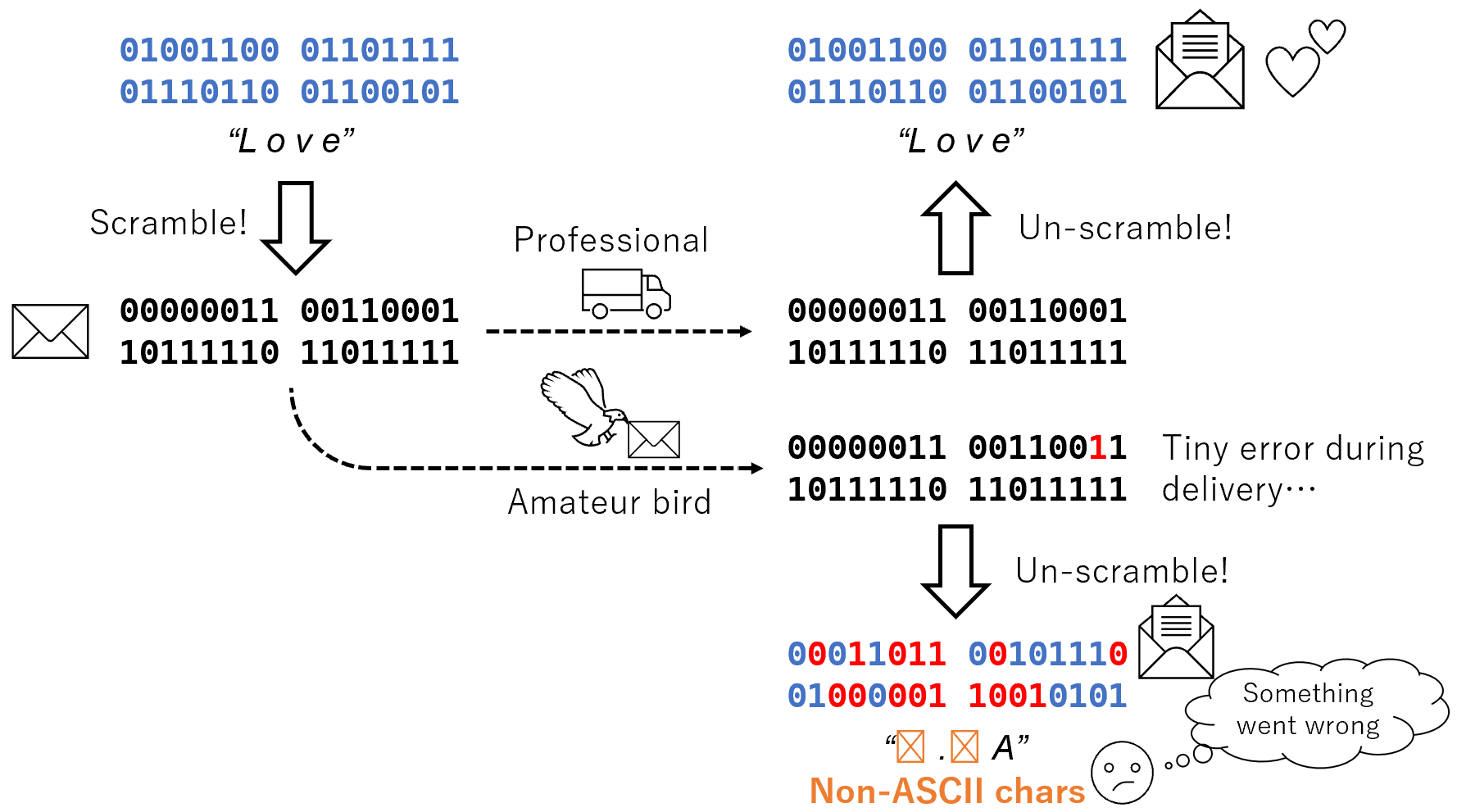
This library performs reversible data scrambling such that a bit error in any location affects the whole bytes. No heavy computation, only addition and lookup table is used. Because even a tiny bit error turns the entire data into a completely different one, error detection can be performed without excess bits, thanks to the potential constraints of the data.

Principle: we may put very strong constraints on data

We have ASCII codes to represent strings. The number of ASCII codes that correspond to actual characters is 100 (33 to 126 for characters, and Space, CR, LF, Tab, NUL), and usually one byte is allocated for each character.

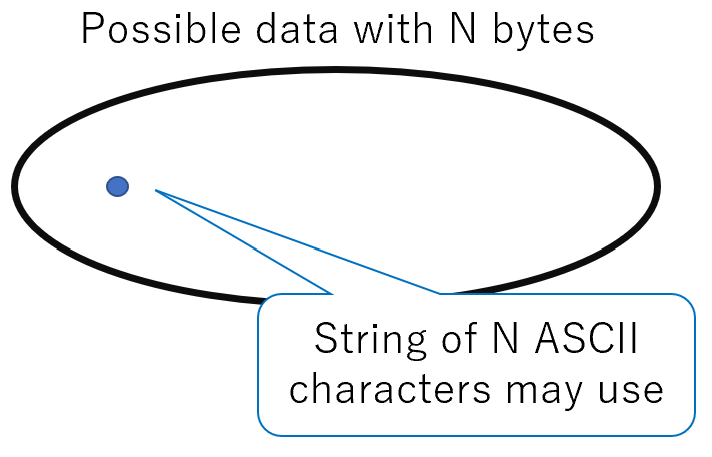
Essentially, one byte can represent 256 different numbers, so less than half of the numbers are effectively used. In more detail, there is a 99/256 = 39% probability that a random 1-byte number is a character.

A 10-character string is represented by 10 bytes. But when 10 bytes of data are randomly chosen, the probability that it is a string is only 0.39^10=0.08%. So, we are using very little of the amount of information that a byte sequence has when representing a string of characters.

String is just one example; the JSON format imposes stronger constraints. Binary data is also constrained by its format.

Scrambling and error detection using underlying constraints

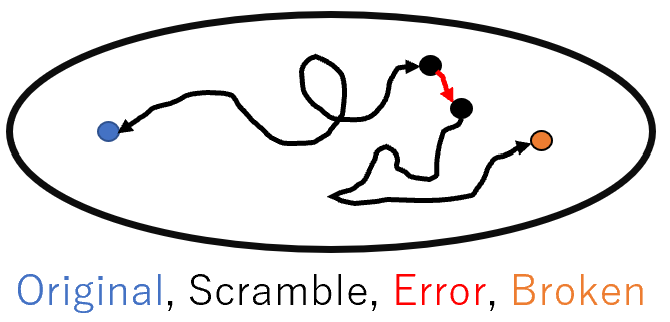
Combining this constraint with a reversible data conversion, where a difference of a single bit can lead to a completely different result (scramble), enables error detection without adding new bits.

First, apply this scrambling to the data. If the data is error-free, applying the reverse scrambling will restore it.

However, if there are errors in the scrambled data, the reverse-scrambled data will be very different from the original data. For example, if the original data is a string, the reverse-scrambled data with errors will be far from a string. Now we can tell that there were errors.

How it works

The algorithm is implemented with just addition and table lookups. No heavy integer computation which is common in cryptographic algorithms is required. The algorithm consists of pseudo-hadamard transform and GF(2^8) table. The pseudo-hadamard transform is recursively applied so that any tiny error affects the entire bytes. Runs in O(N log N) time. Even available in MCU with limited resources.

Applications

• Error detection w/o extra bits: as described above. After the reverse scramble, check whether the restored data satisfies the original format.
• Error detection with additional bits: For data without any constraint, or adding more error detection ability. This can be done by adding some magic numbers along with the original data. Use this number for validation.
  • For example, suppose data with N bits of additional magic number is scrambled. In that case, the probability of getting the same magic number after reverse scramble is 2^(-N) in the random data.

Note that these detection scheme is probabilistic, so rarely (low probability) error is missed

How to use

• C language: include bitsnarl.h and add bitsnarl.c to your project. See example.c for example
• C++ language: header-only library, so just include bitsnarl.hpp. See example.cpp for example

TODO

• Try error correction using SAT or SMT solvers
• Implement in other languages

License

MIT