A bad excuse to learn c++ and openGL.

Why are computer graphics nerds obsessed with turning rabbits into spheres? I think I've figured it out.

I don't think of fractals as being aesthetically interesting, nevertheless this one caught my interest so I tried to make it look good :

The hello world equation with a twist.

The solution of the Poisson equation depends on the global information over the domain, therefore finding a good parallel computing scheme is far from trivial.

Parallel computing of the shallow water equations on the gnomonic equiangular grid, performed by modifying pyRSW, a discrete exterior calculus based model.

Out of the box pyRSW can compute flow on curved surfaces but cannot handle skewed grids, moreover the topology of the cubed sphere asks for tailor-made parallel communications between processes. For this purpose, the module uses a "stairway" cube net in order to simplify the implementation of the communications (see the image below). For now, the cubed sphere module is able to compute surfaces waves correctly. More work is needed to find a consistent reconstruction of fluid velocity at the grid vertices to handle the vorticity induced by the rotation of the sphere. This issue is due to the severe non-orthogonality at the corners of the cube's faces. Link to the AGU article

My first personal code project, which I implemented after getting a bit too interested in the vorticity equation. This program is old and may seem naive, however its implementation uses a less common description of the fluid, which leads to an extremely simple implementation. Nevertheless, the scheme uses finite differences and an explicit time integration, which result in a quite unstable computation.

With the help of Malo Kerebel

This is one of the first projects I participated in.

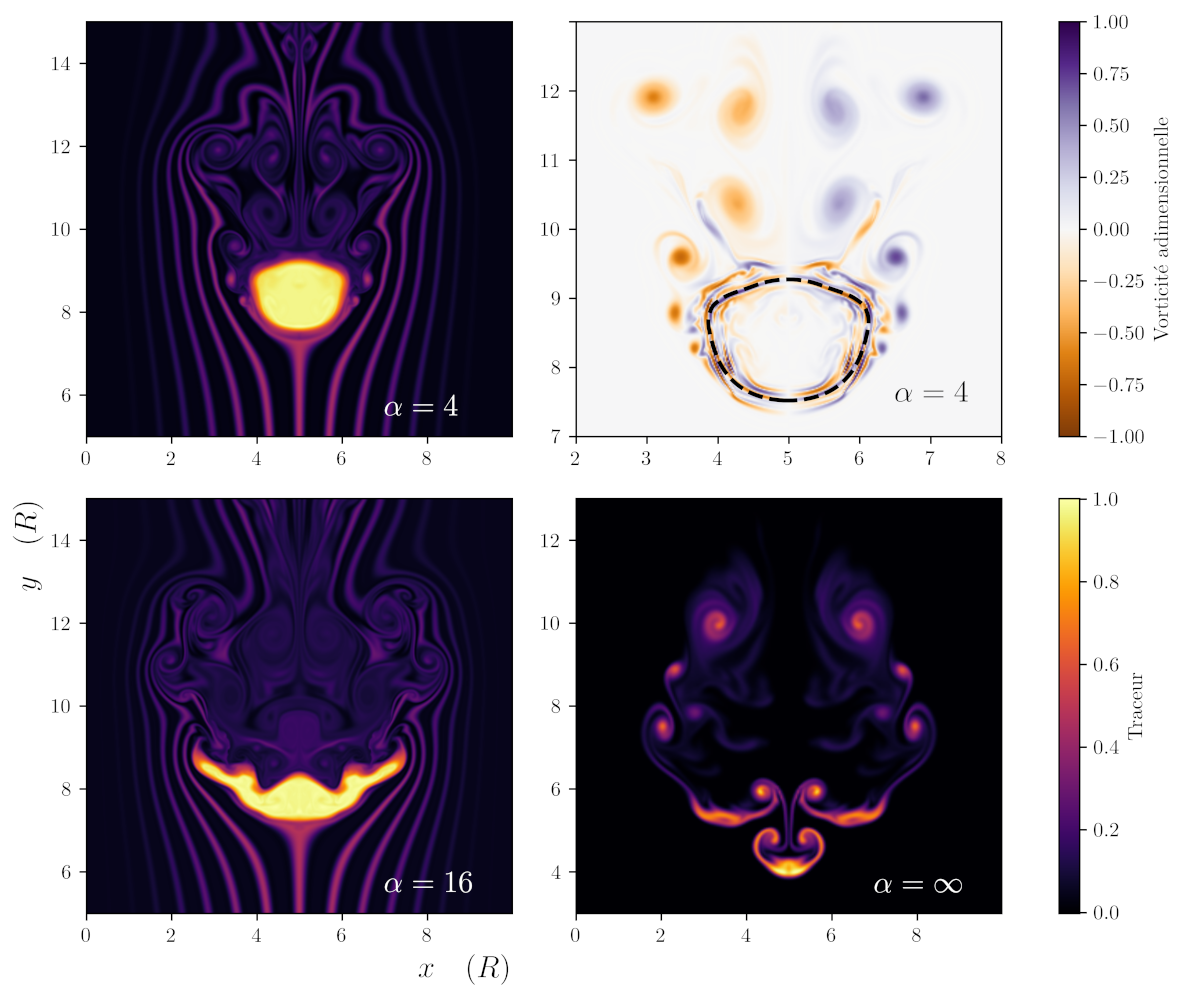
Here we tried to implement an Eulerian description of the droplet interface using the level-set method in the context of the Boussinesq approximation of the Navier-Stockes equations, i.e., for small changes of buoyancy. This led us to :

• Painfully rediscover the Eötvös number (Eo, which we called α in the image below).
• With dismay, find by a simple geometric argument that in order to get an O(h²) convergence on the curvature estimation, O(h⁴) convergence is needed on the interface location.
• For small Eötvös numbers, i.e., when the volume forces are small in comparison to the surface tension, it is extremely difficult to find a stable numerical scheme.
• Conclude that using a vorticity based model and the Boussinesq approximation is one of the worst cases to implement a multiphase flow simulation.